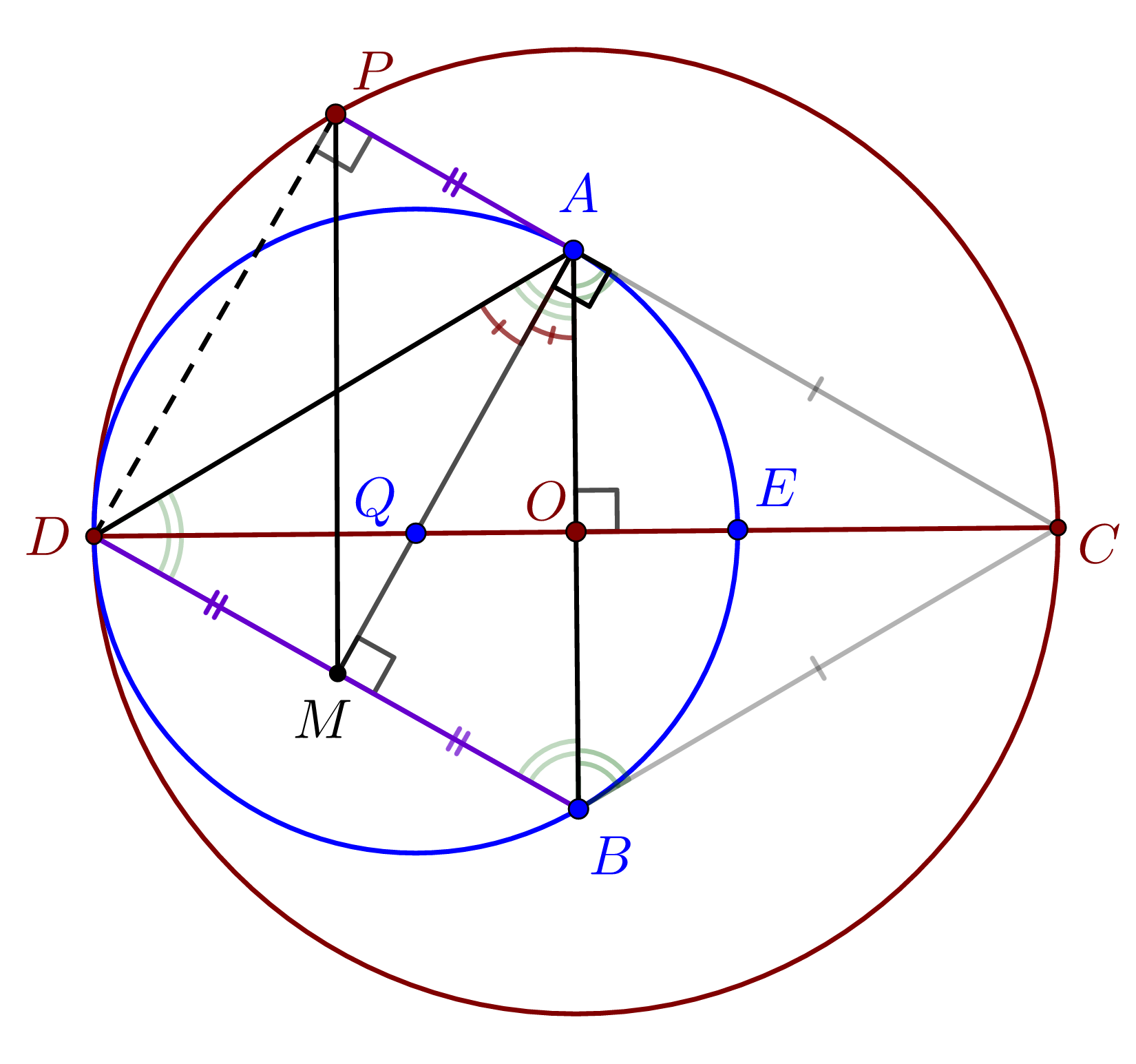
În figura de mai jos cercurile C(Q) și C(O) sunt tangente interior în punctul D. C este un punct de pe cercul C(O). CA și
Autor: Anca

Cercul a fost studiat încă de la începuturile istoriei. Înțelegerea sa a stat la baza multor invenții practice, de exemplu a roții, precum și la
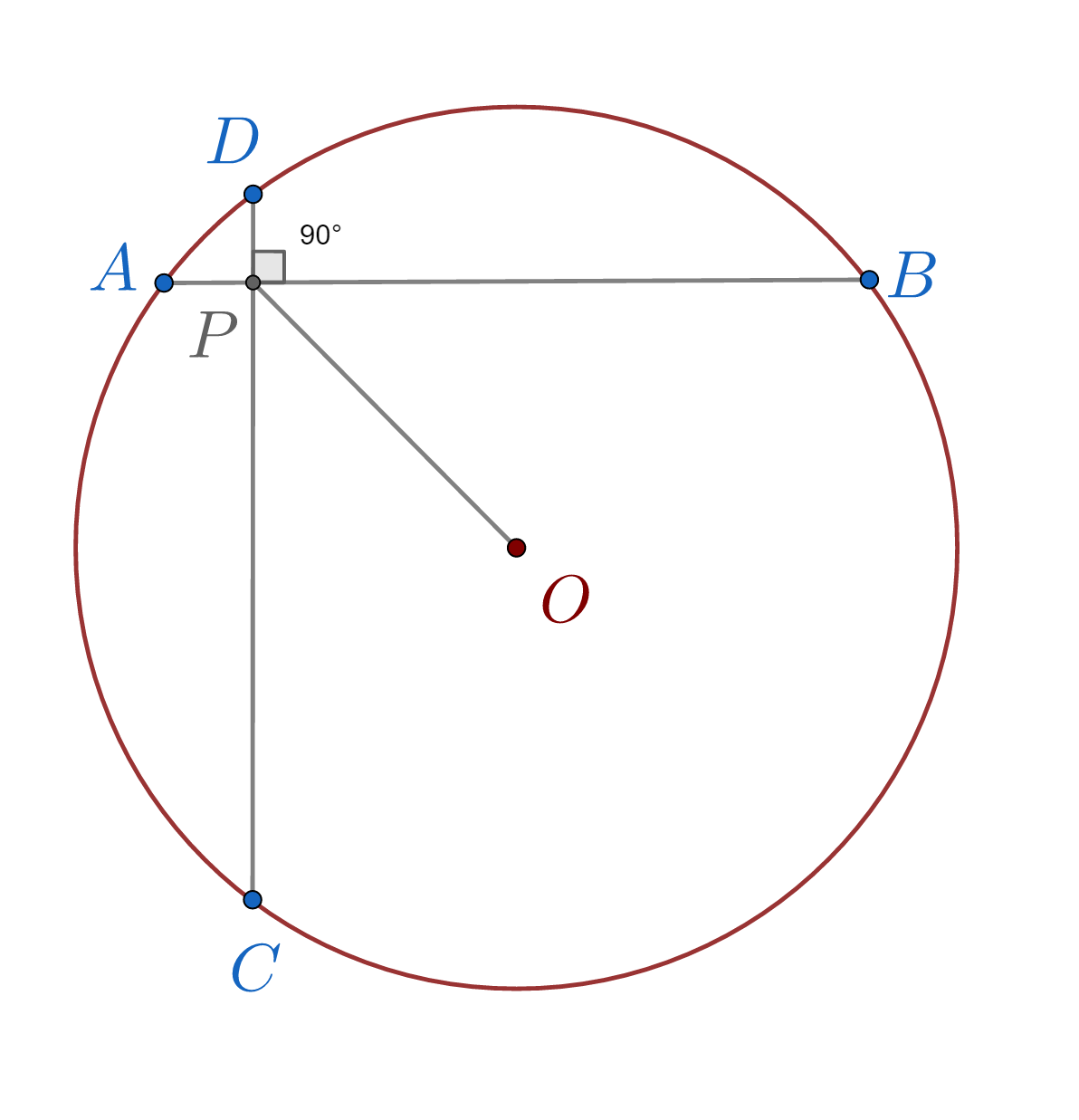
În figura de mai jos sunt desenate două coarde perpendiculare AB=CD =8cm, în cercul cu centrul în O și raza de 5cm. Dacă P este
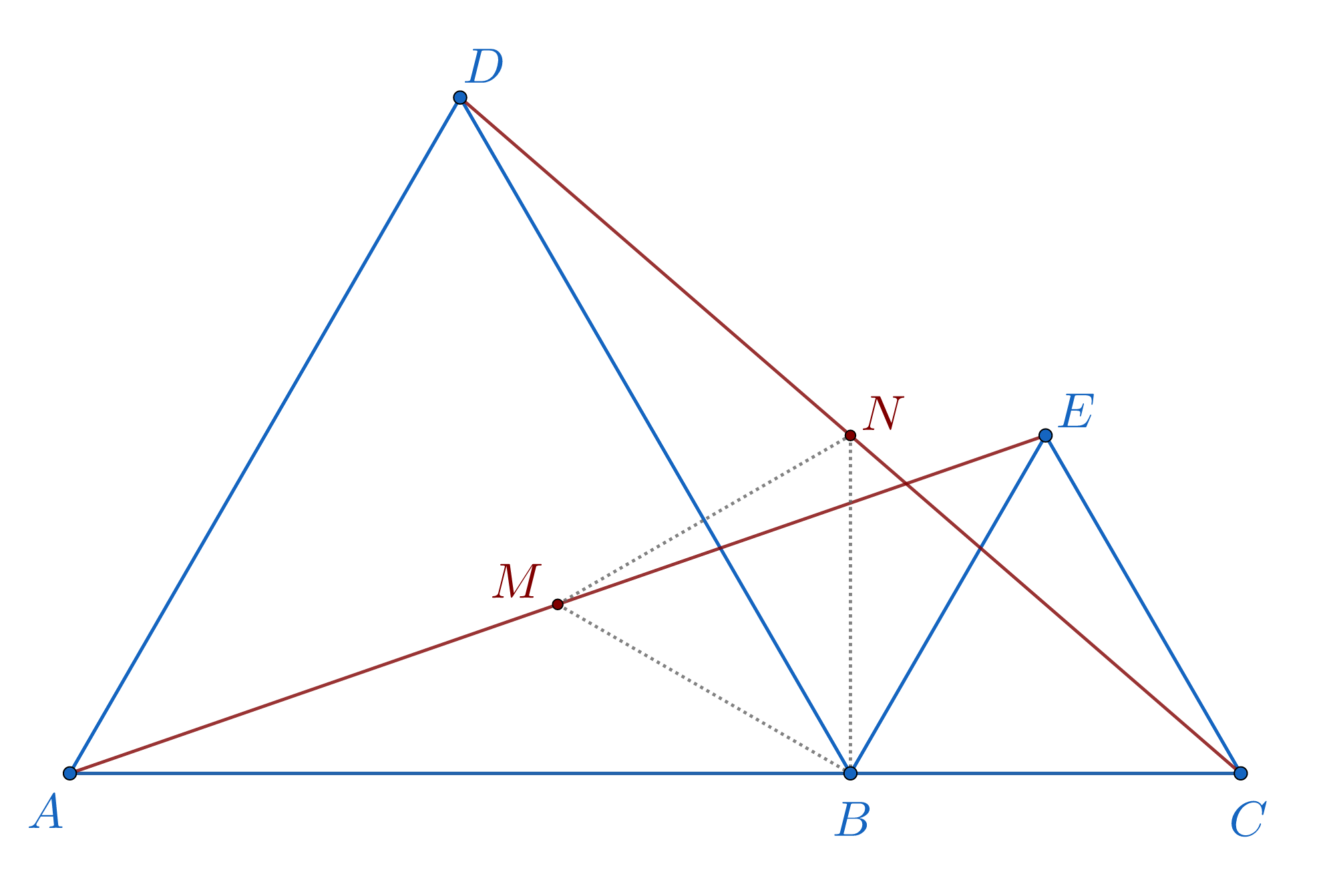
În figura de mai jos, atât triunghiul ABD cât și triunghiul BCE sunt echilaterale. Punctul B aparține lui (AC), AB = 12 cm și BC
Cele 16 teoreme descrise mai jos ne ajută în rezolvarea și înțelegerea multor probleme despre triunghiul oarecare, dar mai întâi să vedem care sunt liniile

Găsiți mai jos cele mai cunoscute inegalități necesare pentru rezolvarea rapidă a multor probleme. 1. Inegalitatea mediilor: Media aritmetică, media geometrică, media armonică poartă numele de medii

Să se demonstreze: Demonstrăm întai a doua inegalitate: Din inegalitatea Cauchy-Buniakovski-Schwarz știm că: Dacă bi este 1 pentru oricare i inegalitatea devine: Demonstrăm prima inegalitate:

Vrem să calculăm aria triunghiului oarecare ABC: notăm cu a lungimea laturii opuse unghiului A, cu b lungimea laturii opuse unghiurilor B si c lungimea laturii opuse unghiului
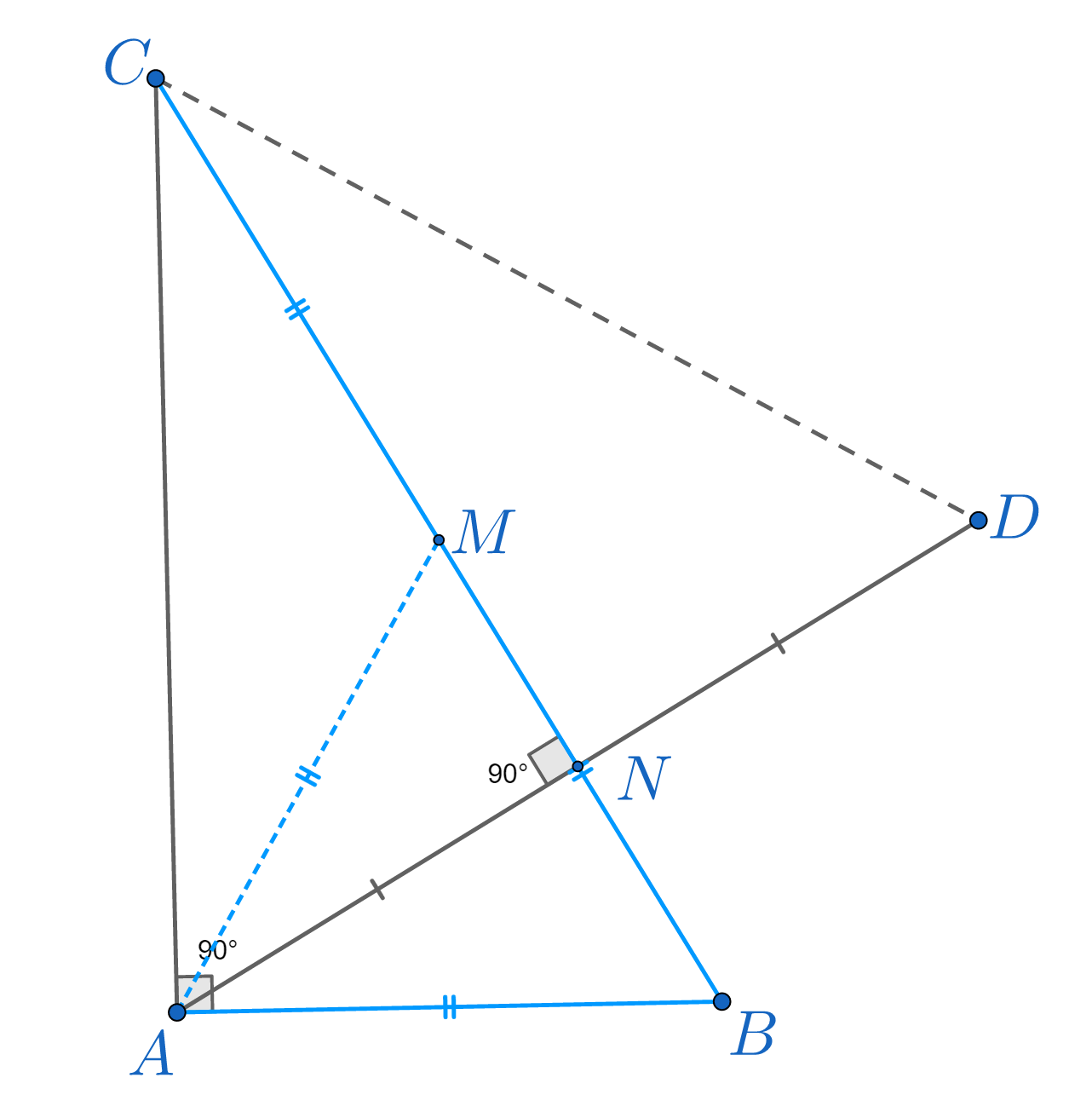
Se consideră triunghiul dreptunghic ABC. Măsura unghiului A este de 900 de grade, BC= 2AB și D simetricul lui A față de BC. a) Demonstrați

Fie triunghiul dreptunghic ABC cu măsura unghiului A de 90o. Latura opusă unghiului de 90o , BC, se numește ipotenuză. AB și AC se numesc