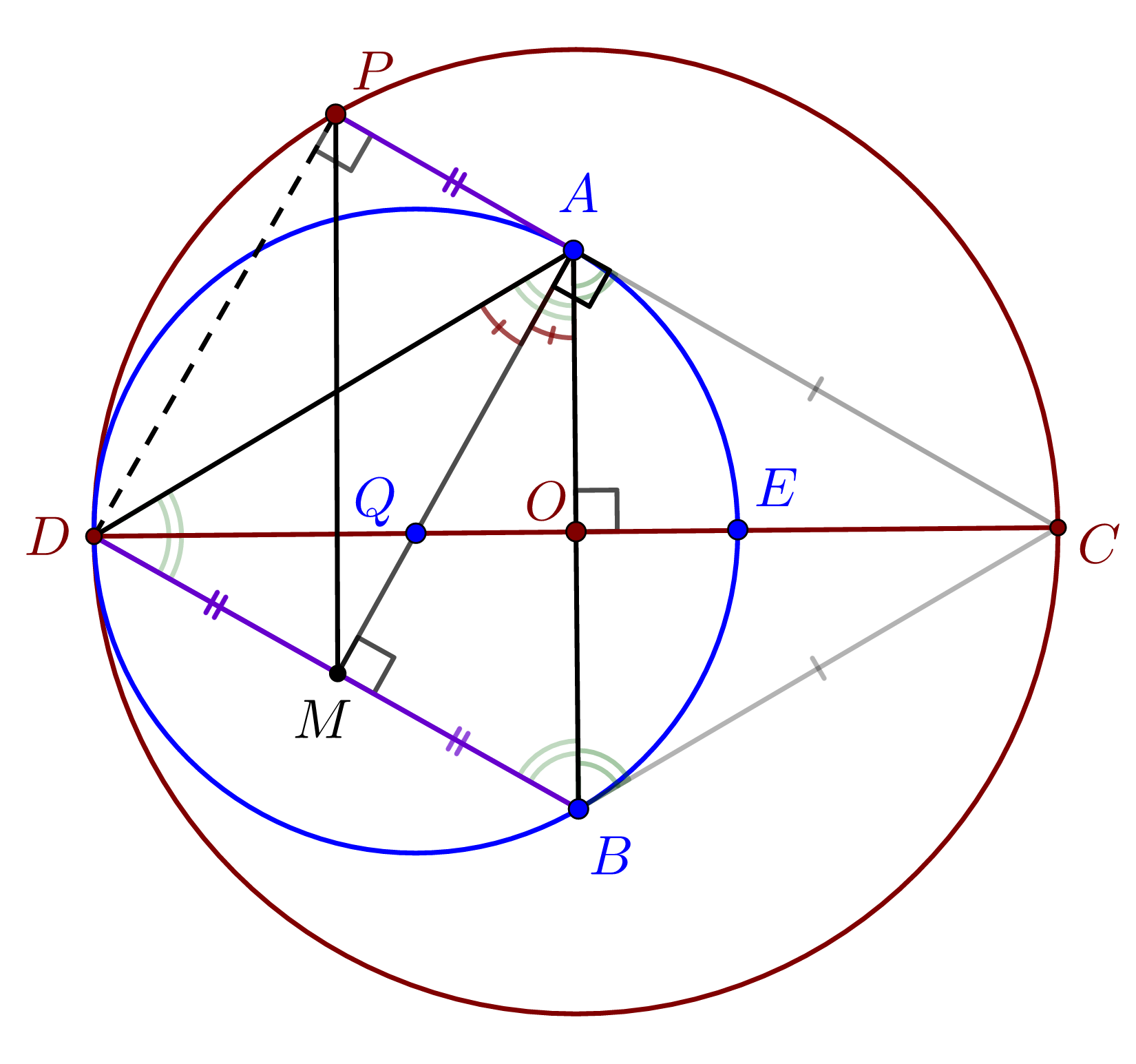
În figura de mai jos cercurile C(Q) și C(O) sunt tangente interior în punctul D. C este un punct de pe cercul C(O). CA și CB sunt tangentele din punctul C la cercul C(Q). Punctul D este diametral opus punctului C, iar intersecția dintre AB și DC este în punctul O.
a) Stabiliți natura triunghiului ABC.
b) Dacă punctul P se află la intersecția dintre AC și cercul C(O) și M se află la intersecția dintre AQ și DB, arătați că MP este perpendicular pe CD.
a) Din teorema ciocului de cioara AC = BC.
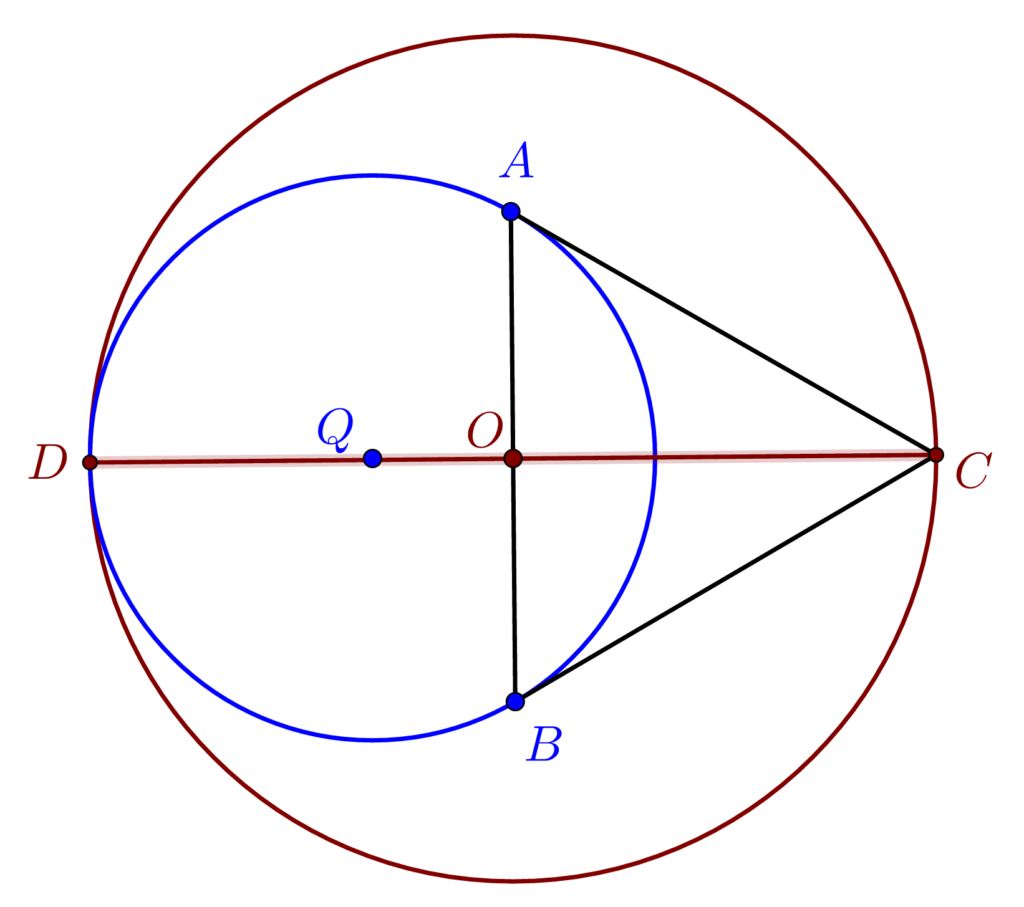
Pentru a demonstra punctul a)
Știm că dacă ducem dintr-un un punct exterior cercului cele două tangente la cerc atunci lungimile segmentelor formate de punctul exterior și punctele de tangență sunt egale (Teorema ciocului de cioară). Știm de asemenea că tangenta este perpendiculară pe raza cercului dusă în punctul de tangență.
Ne vom folosi de unele teoreme și formule și despre cerc.
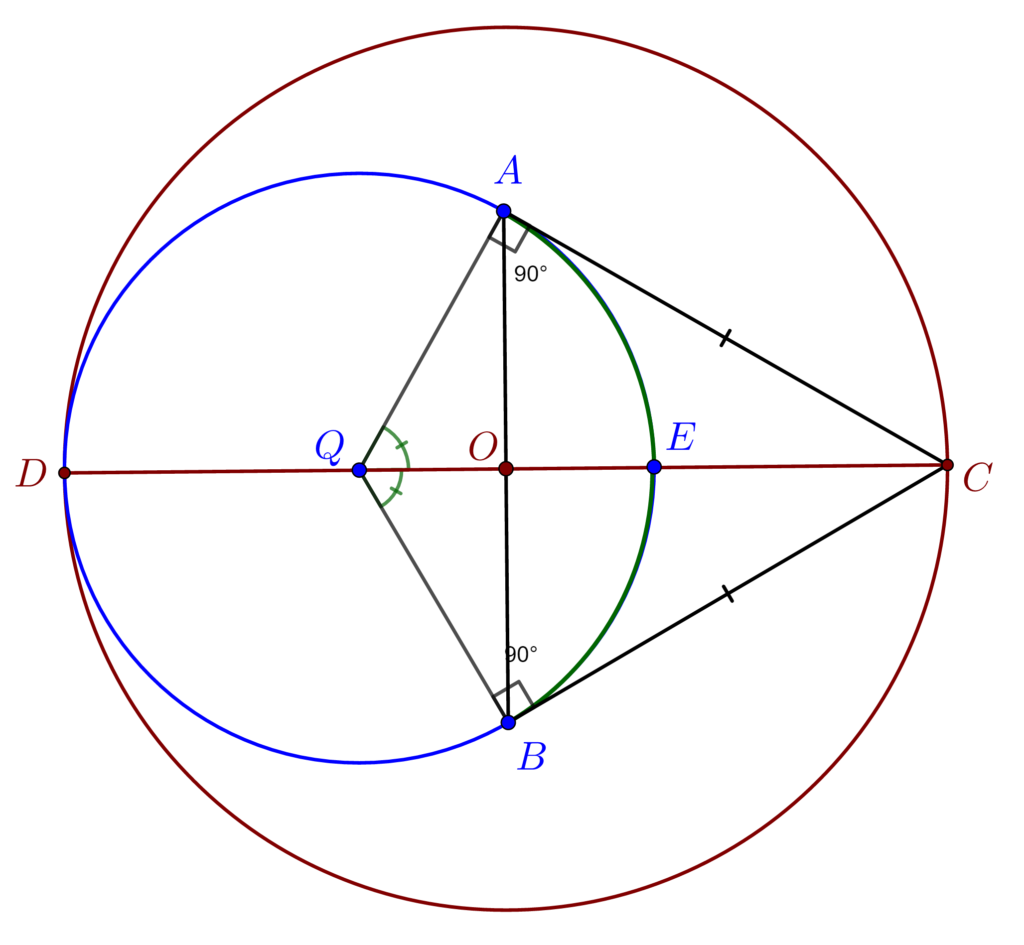
CA \;și\; CB\;tangente\\din\;punctul\;C\;la\; C(Q)\;\;\overset{th.\;Ciocului\;de\;Cioara}{\implies} \\\;\\\overset{th.\;Ciocului\;de\;Cioara}{\implies}[CA]\equiv [CB]\\\;\\
\left.
\begin{array}{ll}
CA\;tangentă\; la\;C(Q)\\
QA\;rază
\end{array}
\right \} \implies \\\;\\\implies QA \perp AC\\\;\\
\left.
\begin{array}{ll}
CB\;tangentă\; la\;C(Q)\\
QB\;rază
\end{array}
\right \} \implies \\\;\\\implies QB \perp BC\\\;\\
\left.
\begin{array}{ll}
[QA ]\equiv[QB] (raze)\\
[CA]\equiv [CB]\\
m(\measuredangle QAC) = m(\measuredangle QBC) = 90^\circ\\
\end{array}
\right \} \overset{CC}{\implies} \\\;\\\overset{CC} {\implies}m(\measuredangle BQC) = m(\measuredangle AQC) 
[the_ad_group id=”104″]
În același cerc la unghiuri la centru egale corespund arce egale.
Dacă diametrul împarte coarda în doua arce egale atunci diametrul este perpendicular pe coardă.
Diametrul perpendicular pe coardă împarte coarda în două parți egale.
\left.
\begin{array}{ll}
m(\measuredangle BQC) = m(\measuredangle AQC) \\\;\\
\measuredangle BQC\;și\;\measuredangle AQC\\ unghiuri\;la\;centru\;în\; C(Q)
\end{array}
\right \} \implies \\\;\\
\left .
\begin{array}{ll}
\implies m(\overset{\frown}{AE})=m(\overset{\frown}{BE})\\
\;\;\;\;\;\;\;\;DE\;diametru\;în\;C(Q)
\end{array}
\right \} \implies \\\;\\
\left .
\begin{array}{ll}
\implies DE\perp AB \\
\;\;\;\;\;\;\;\;DE\;diametru\;în\;C(Q)
\end{array}
\right \} \implies \\\;\\ \implies [AO]\equiv[BO]\\\;\\
Folosind cazurile de congruență pentru triunghiul dreptunghic vom arăta că AD, AC, BD și BC sunt egale.
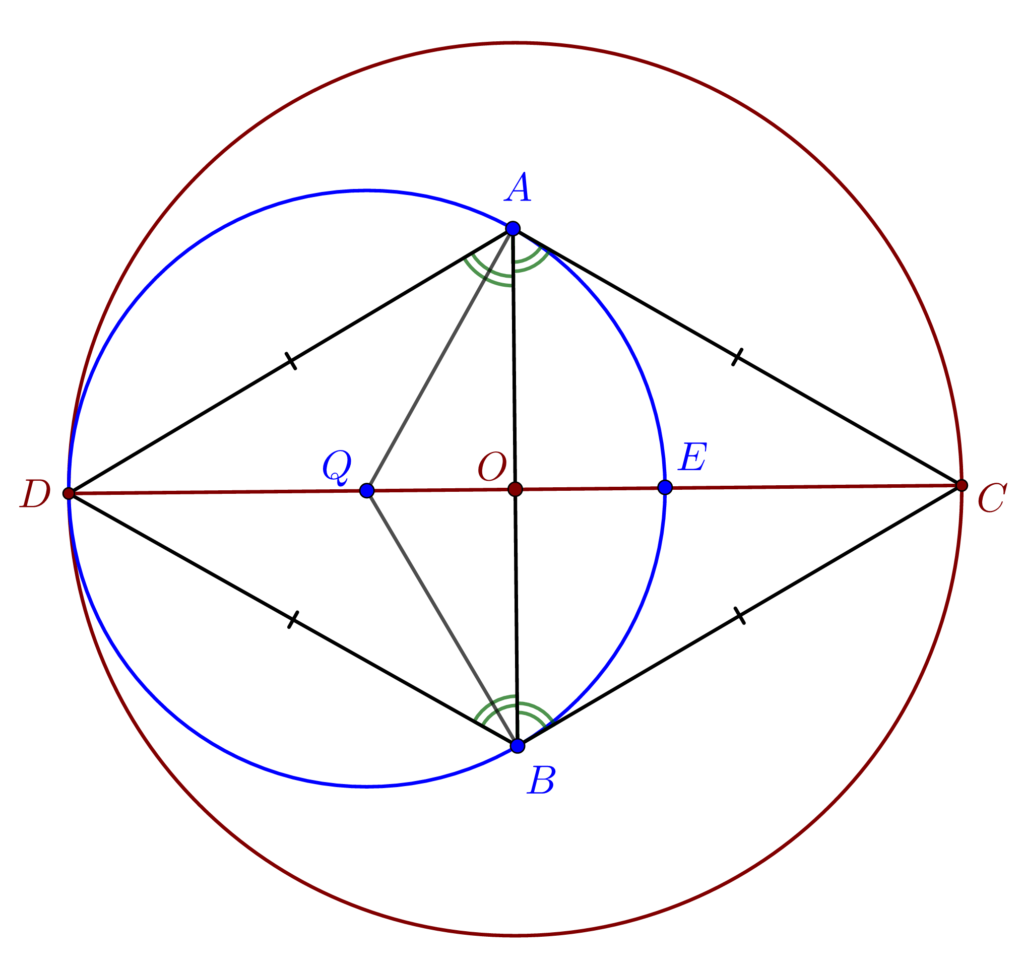
\left .
\begin{array}{ll}
am\;arătat\;că\;AO\perp DE\\
[DO] \equiv [OC] (raze \;în \;C(O))\\
AO\; lat\;comună
\end{array}
\right \} \overset {CC}{\implies} \\\;\\\overset {CC}{\implies} △ AOD \equiv△ AOC \implies \\\;\\\implies
\left \{
\begin{array}{ll}
m(\measuredangle DAO) = m(\measuredangle CAO) \\\;\\
[DA]\equiv[CA]
\end{array}
\right .
\\\;\\analog\;demonstrăm\;că:\\\;\\
\left \{
\begin{array}{ll}
m(\measuredangle DBO) = m(\measuredangle CBO) \\\;\\
[DB]\equiv[CB]
\end{array}
\right . \\\;\\
\left .
\begin{array}{ll}
AO\perp DC\\
[AC] \equiv [BC] (th.\;Ciocului\;de\;cioară)\\
OC\; lat\;comună
\end{array}
\right \} \overset {CI}{\implies} \\\;\\\overset {CC}{\implies} △ AOC\equiv△ BOC \implies \\\\implies m(\measuredangle CAO) = m(\measuredangle CBO)\\\;\\
\left .
\begin{array}{ll}
[AC] \equiv [BC] (th.\;Ciocului\;de\;cioară)\\
[DB]\equiv[CB]\\
[DA]\equiv[CA]\\
\end{array}
\right \}
\implies \\\;\\\implies
[DA]\equiv[DB]\\
Articolul continuă pe pagina următoare