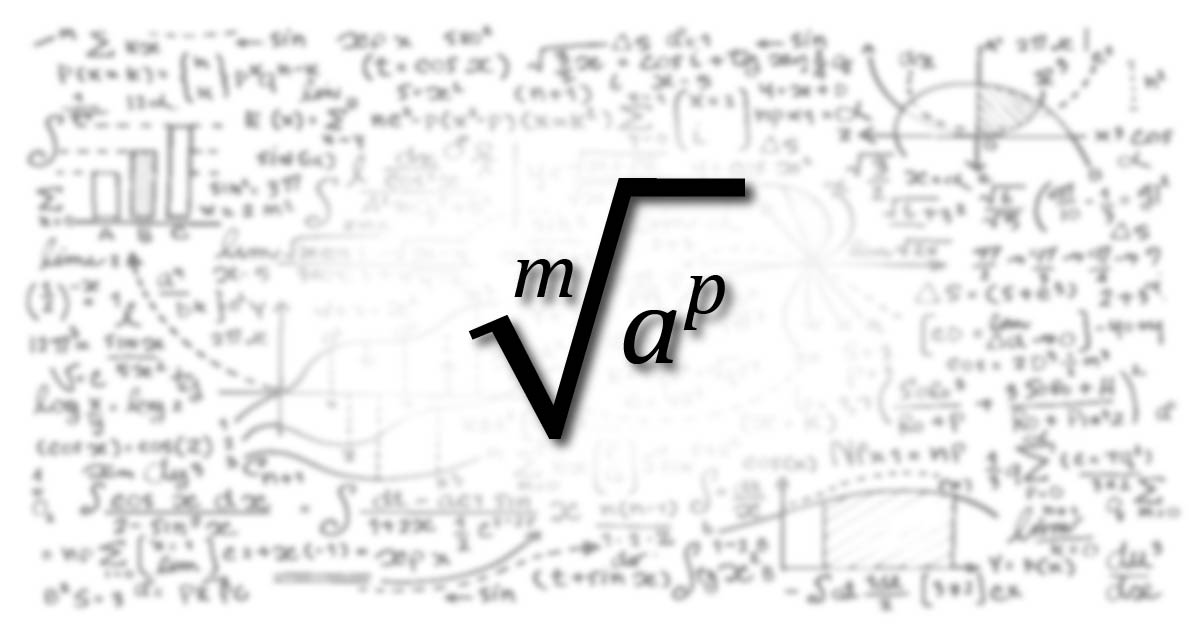Radicalul unui număr reprezintă un alt număr, care ridicat la o putere cu exponent fracționar (numitorul exponentului puterii fiind denumit ordinul radicalului) este egal cu numărul dat. Dacă ordinul nu este precizat, atunci este vorba implicit de radicali de ordinul 2 (sau rădăcină pătrată).
Fie a un număr real pozitiv, a ∈ ℝ+, și n un număr natural nenul, n ∈ ℕ*. Se numește radical de ordinul 2n (par) acel număr pozitiv b pentru care b2n = a.
Fie a un număr real, a ∈ ℝ, și n un număr natural nenul, n ∈ ℕ*, se numește radical de ordinul 2n+1 (impar) acel număr pozitiv b pentru care b2n+1 = a.
Observăm că
- dacă ordinul radicalului este par atunci exista radical de ordin par din a doar dacă a este pozitiv.
- ordinul radicalului este mai mare sau egal cu 2
- radicali sau rădăcini – aceste denumiri sunt sinonime.
Notație
Notăm cu \sqrt[n]{x} radicalul de ordin n din x sau rădăcina de ordinul n a lui x.
Proprietățile principale pentru radicali
Pentru egalitățile de mai jos vom considera coeficienții radicalilor m și n numere naturale mai mari sau egale cu 2; m ,n \in\N, m, n\ge2
\begin{alignedat}{2} \textbf{ 1. } &\sqrt[m]{a}= a^\frac{1}{m}; \ a \geq 0 \\[1em] \textbf{ 2. }&\sqrt[m]{\frac{1}{a}}= \frac{1}{\sqrt[m]{a}} =a^{-\frac{1}{m}};\ a >0 \\[1em] \textbf{ 3. } &(\sqrt[m]{a})^m= a; \ a \geq 0 \\[1em] \textbf{4. }& \text{ Produsul radicalilor este egal cu radicalul produsului }\\ & \text{ - daca m este par}:\\ &(\sqrt[m]{a})\cdot (\sqrt[m]{b})= \sqrt[m]{a\cdot b}; \ a , \ b \geq 0 \\ &(\sqrt[m]{|a|})\cdot (\sqrt[m]{|b|})= \sqrt[m]{a\cdot b}; \ a\cdot b \geq 0 \\[1em] & \text{ - daca m este impar}:\\ &(\sqrt[m]{a})\cdot (\sqrt[m]{b})= \sqrt[m]{a\cdot b}; (\forall) \ a , \ b \in \R \\[1em] \textbf{5. } &(\sqrt[m]{a})\cdot (\sqrt[m]{b}) \cdot (\sqrt[m]{c})= \sqrt[m]{a \cdot b \cdot c}; \ \ a , b, c \geq 0 \\[1em] \textbf{6. }&\bigg(\sqrt[m]{\frac{1}{a}}\bigg)^m= \frac{1}{a};\ a >0 \\[1em] \textbf{7. } &\text{ Câtul radicalilor este egal cu radicalul câtului}\\ & \text{ - daca m este par}:\\ &\sqrt[m]{a}:\sqrt[m]{b}= \frac{\sqrt[m]a}{\sqrt[m]b} = \sqrt[m]{\frac{a}{b}}; \ a \geq 0, \ b >0\\[1em] &\sqrt[m]{\frac{a}{b}} = \frac{\sqrt[m]{|a|}}{\sqrt[m]{|b|}}; \ a \cdot b \geq0, \ b \neq0\ \\[1em] \textbf{8. } &\sqrt[m]{a} \cdot\sqrt[n]{a}= \sqrt[mn]{a^{m+n}} ;\ a \geq 0 \\[1em] \textbf{9. } &\sqrt[m]{a} :\sqrt[n]{a}= \sqrt[mn]{a^{n-m}}; \ a > 0 \\[1em] \textbf{10. } &\sqrt[m]{a^{n}}= (\sqrt[m]{a})^n = a^{\frac{n}{m}}; \ a \geq 0\\[1em] \textbf{11. } & \text{ Simplificarea ordinului radicalului}\\[1em] &\ \sqrt[n]{a^{nm}}= a^{m} ;\ a \geq 0 \\[1em] &\sqrt[mn]{a^{mp}}= \sqrt[n]{a^p}; \ a \geq 0\\[1em] \textbf{12. } & \text{Aducerea radicalilor la același ordin } \\[1em] &\sqrt[m]{a^{p}}\cdot\sqrt[n]{b^{q}}\ = \sqrt[mn]{a^{pn}\cdot b^{mq}}; \ a \geq 0, \ b \geq 0\\[1em] \textbf{13. } & \text{Extragerea unui radical din alt radical} \\[1em] &\sqrt[m]{\sqrt[n]a}\ = \sqrt[mn]{a} = \sqrt[n]{\sqrt[m]a}; \ a \geq 0 \\[1em] \textbf{14. } &\sqrt[m]{a^{p}} :\sqrt[n]{b^{q}}\ = \sqrt[mn]{a^{pn}: b^{mq}}; \ a, b \geq 0 \\[1em] \end{alignedat} \\ \begin{alignedat}{2} \textbf{15. } &\sqrt[2n]{a^{2n}}= |a|; \ a \in \R \\[1em] &\ \sqrt[]{a^2}= |a|; \ a \in \R \\[1em] \end{alignedat} \\Mai multe proprietăți ale modulului unui număr real puteți găsi aici.
\begin{alignedat}{2} \textbf{16. } &\sqrt[2n+1]{-a}= -a^{\frac{1}{2n+1}}=-\sqrt[2n+1]{a} ; \ a \geq 0 \\[1em] \textbf{17. } &(\sqrt[2n+1]{-a})^{2n+1}= -a ; \ a \geq 0 \\[1em] \textbf{18. } &\sqrt[]{a} + \sqrt[]{b} = \sqrt[]{a + b +2 \cdot \sqrt[]{ab}} ; \ a, b \geq 0 \\[1em] \textbf{19. } &\text{ Expresia conjugată }\\ & \text{ pentru } \ \sqrt[]{a} + \sqrt[]{b}\ \text{ este }\ \sqrt[]{a} - \sqrt[]{b} ; \ a, b \geq 0 \\ & \text{ pentru }\ \sqrt[]{a} - \sqrt[]{b}\ \text{ este }\ \sqrt[]{a} + \sqrt[]{b} ; \ a, b \geq 0 \\ & \text{ pentru } \ \sqrt[3]{a} + \sqrt[3]{b}\ \text{ este }\ \sqrt[3]{a^2} - \sqrt[3]{ab}+\sqrt[3]{b^2} ; \ a, b \geq 0 \\ & \text{ pentru } \ \sqrt[3]{a} - \sqrt[3]{b}\ \text{ este }\ \sqrt[3]{a^2} + \sqrt[3]{ab}+\sqrt[3]{b^2} ; \ a, b \geq 0 \\[1em] \textbf{20. } &\sqrt[]{A + P\cdot\sqrt[]{B} }= \sqrt[]{\dfrac{A+C}{2}} + \sqrt[]{\dfrac{A-C}{2}} \iff \sqrt[]{A^2 -P^2B} = C \\[1em] &\sqrt[]{A - P\cdot\sqrt[]{B} }= \sqrt[]{\dfrac{A+C}{2}} - \sqrt[]{\dfrac{A-C}{2}} \ \iff \sqrt[]{A^2 -P^2B} = C \\ &B \geq 0, A - C \geq 0, A- \sqrt[]B \geq 0 \\[1em] \textbf{21. } &\sqrt[]{A + \sqrt[]{B} }= \sqrt[]{\dfrac{A+C}{2}} + \sqrt[]{\dfrac{A-C}{2}} \iff \sqrt[]{A^2 -B} = C \\[1em] &\sqrt[]{A - \sqrt[]{B} }= \sqrt[]{\dfrac{A+C}{2}} - \sqrt[]{\dfrac{A-C}{2}} \ \iff \sqrt[]{A^2 -B }= C \\ &B \geq 0, A - C \geq 0, A- \sqrt[]B \geq 0 \end{alignedat} \\