Cercul a fost studiat încă de la începuturile istoriei. Înțelegerea sa a stat la baza multor invenții practice, de exemplu a roții, precum și la dezvoltarea unor domenii precum astronomia, geometria și trigonometria. În 1700 î.e.n un papirus egiptean prezintă o metodă de a calcula aria unui disc, aproximând valoare constantei π la 256/81 (3.16049), iar în jurul anului 300 î.e.n, în cartea a III-a din Elementele lui Euclid sunt prezentate proprietățile de bază ale cercului.
Definiții
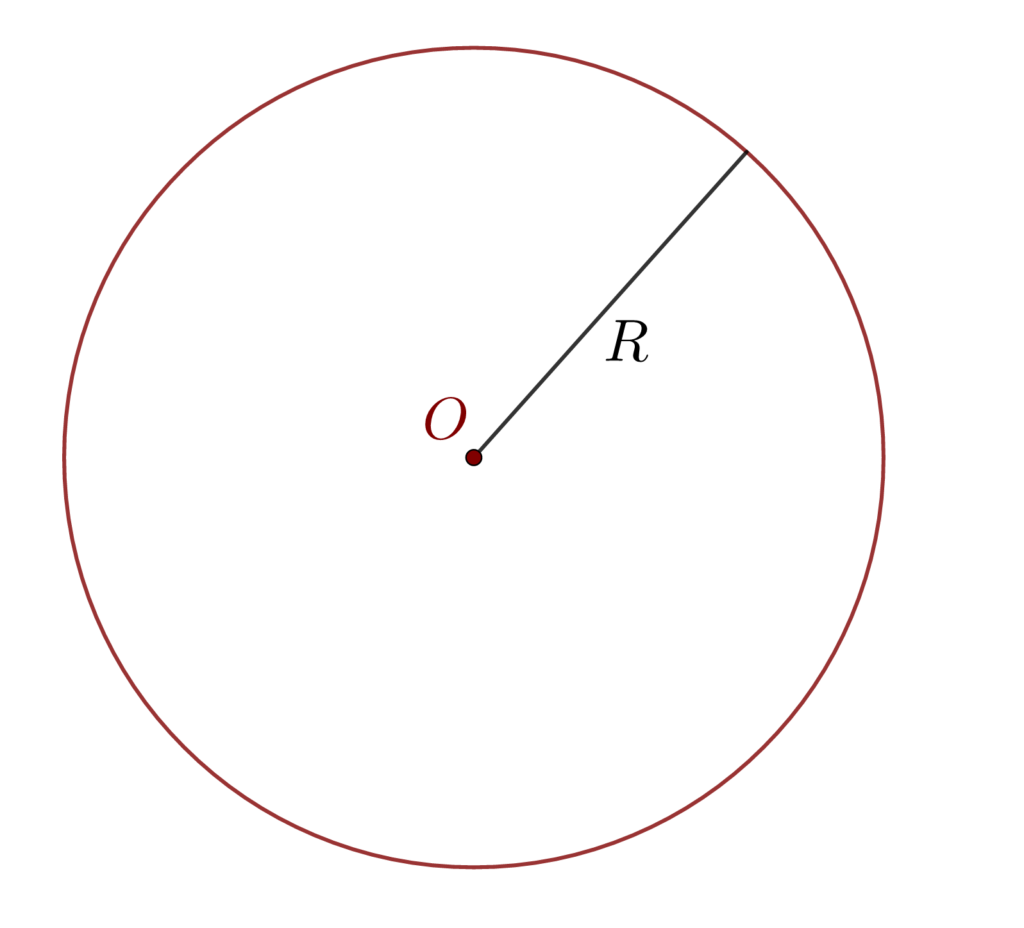
- Cercul este mulțimea punctelor din plan egal depărtate de un punct fix numit centrul cercului. Mai spunem că cercul este locul geometric al punctelor situate la distanta R față de un punct fix O numit centrul cercului.
- Distanța de la centrul cercului la un punct de pe cerc se numește raza cercului.
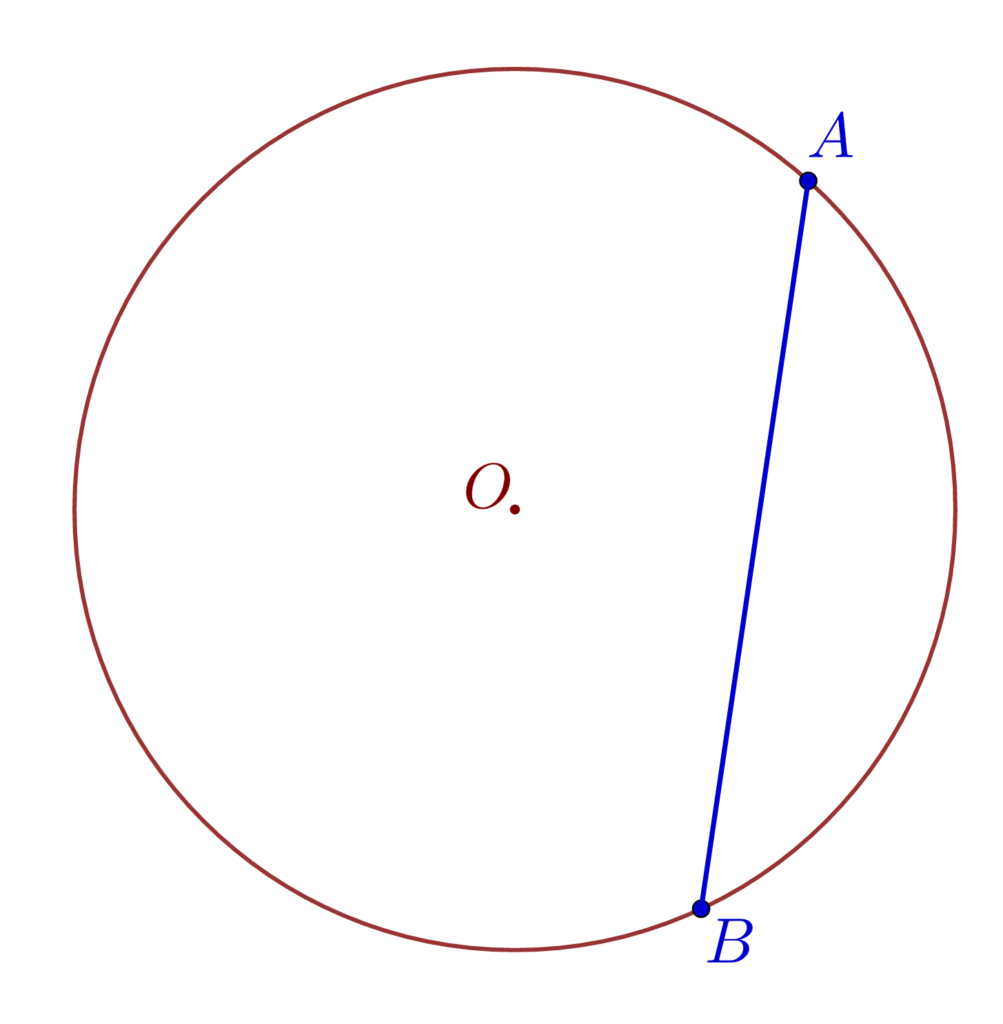
- Coarda este segmentul care unește două puncte distincte de pe cerc.
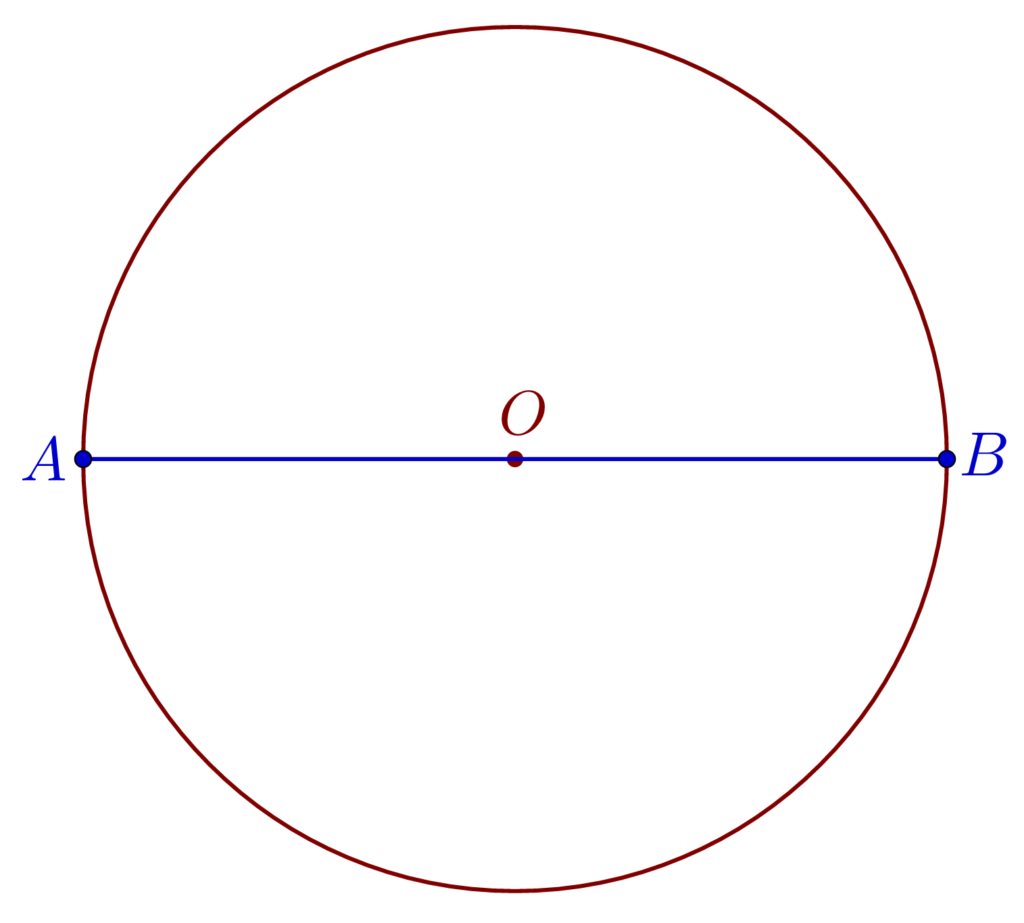
- Coarda care trece prin centrul cercului se numește diametrul cercului. Diametrul este cea mai lungă coardă, fiind dublul razei.
- Discul este regiunea delimitată de un cerc, aflată în interiorul acestuia.

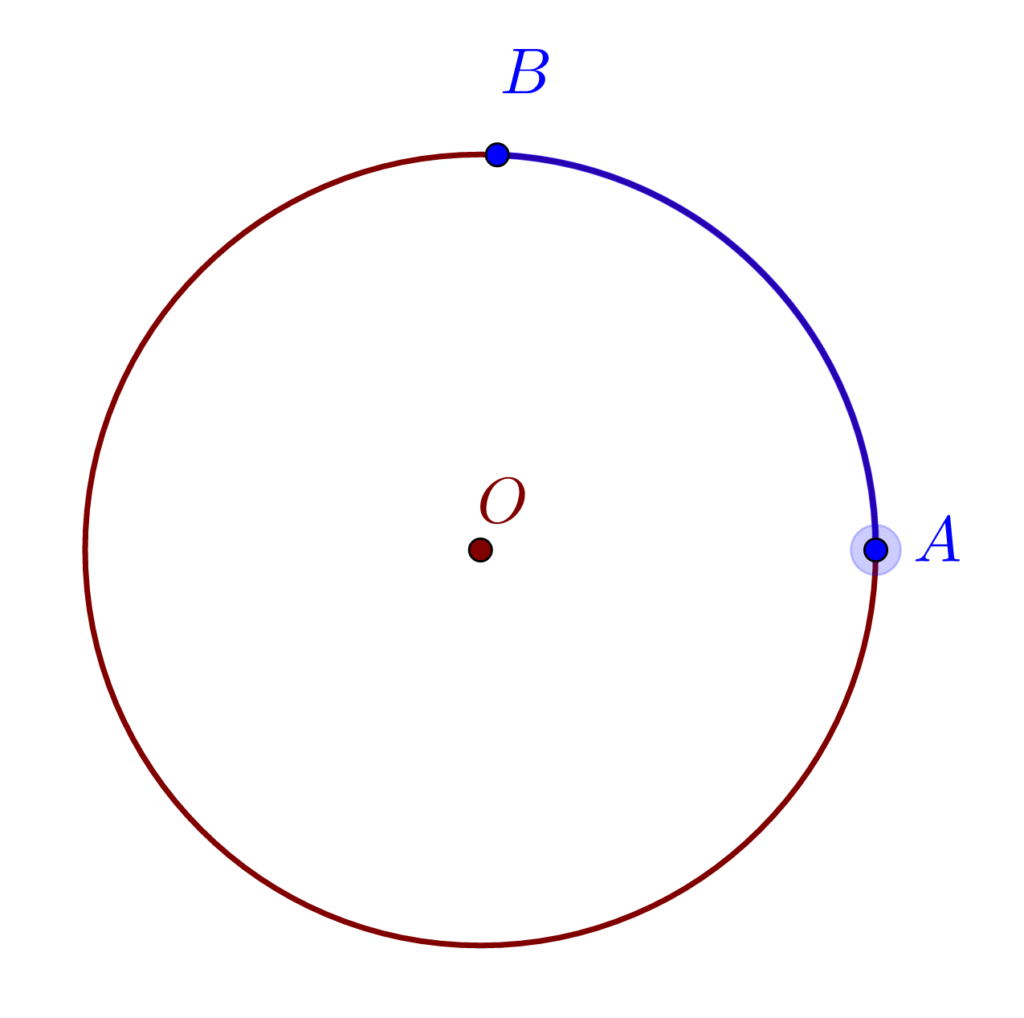
- Porțiunea dintr-un cerc cuprinsă între două puncte distincte se numește arc de cerc. Două puncte de pe circumferința cercului o împart în două arce.
- Două raze împart discul în două sectoare de cerc.
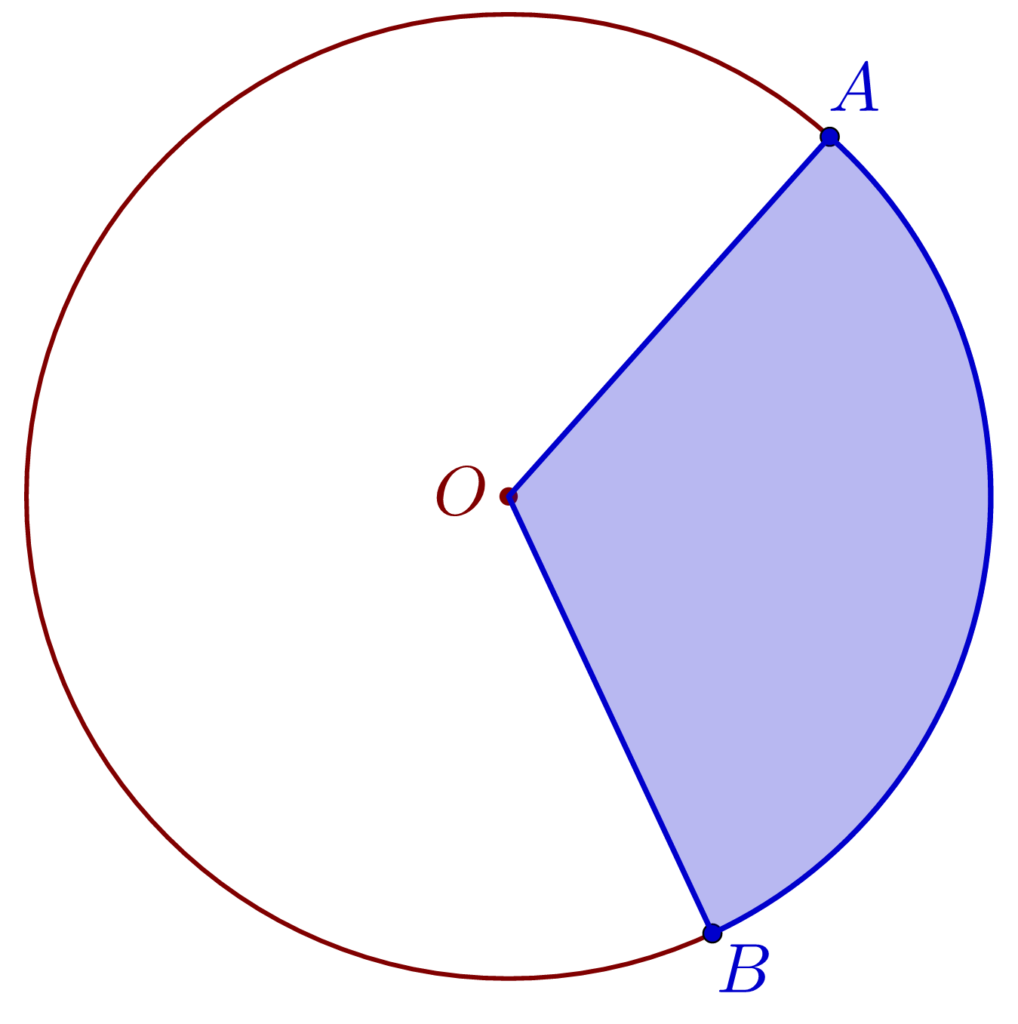
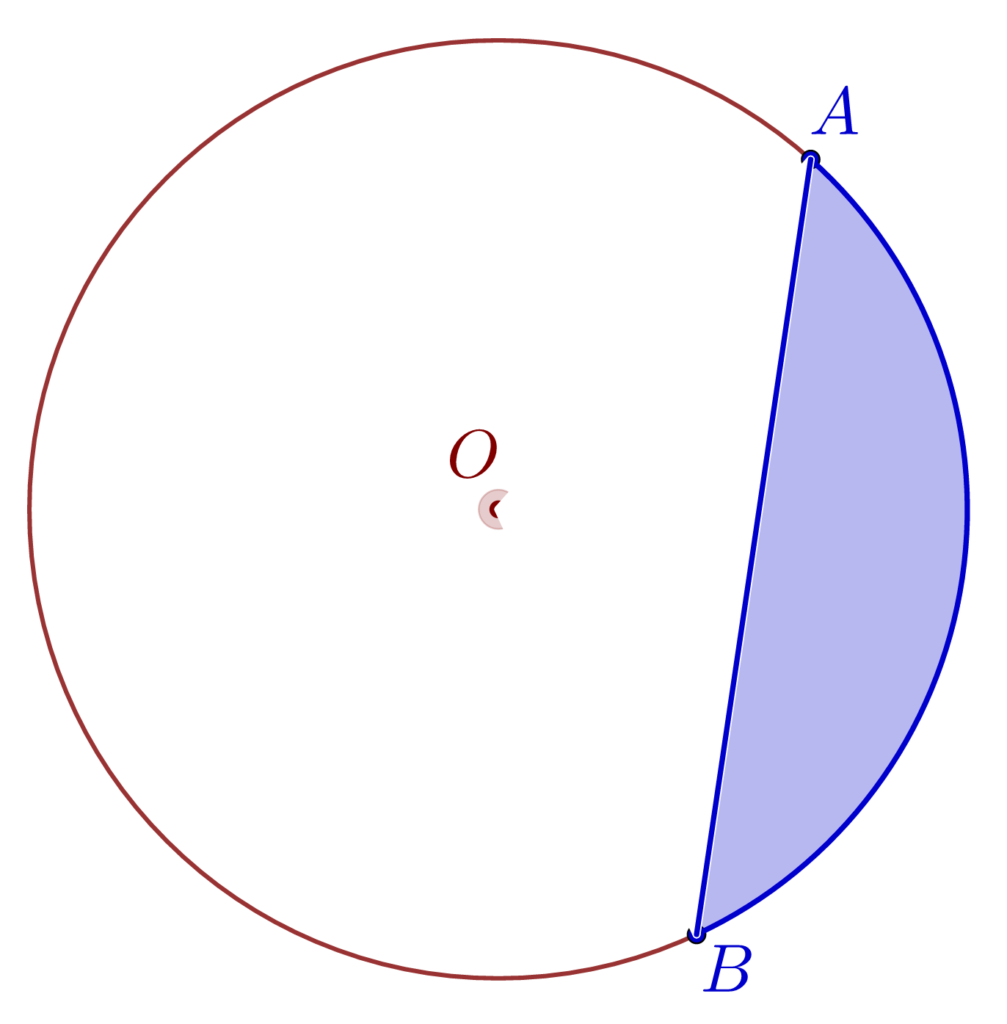
- Un segment circular este o regiune a discului delimitată de un arc de cerc și o coardă care au extremități comune. O coardă împarte cercul în două segmente.
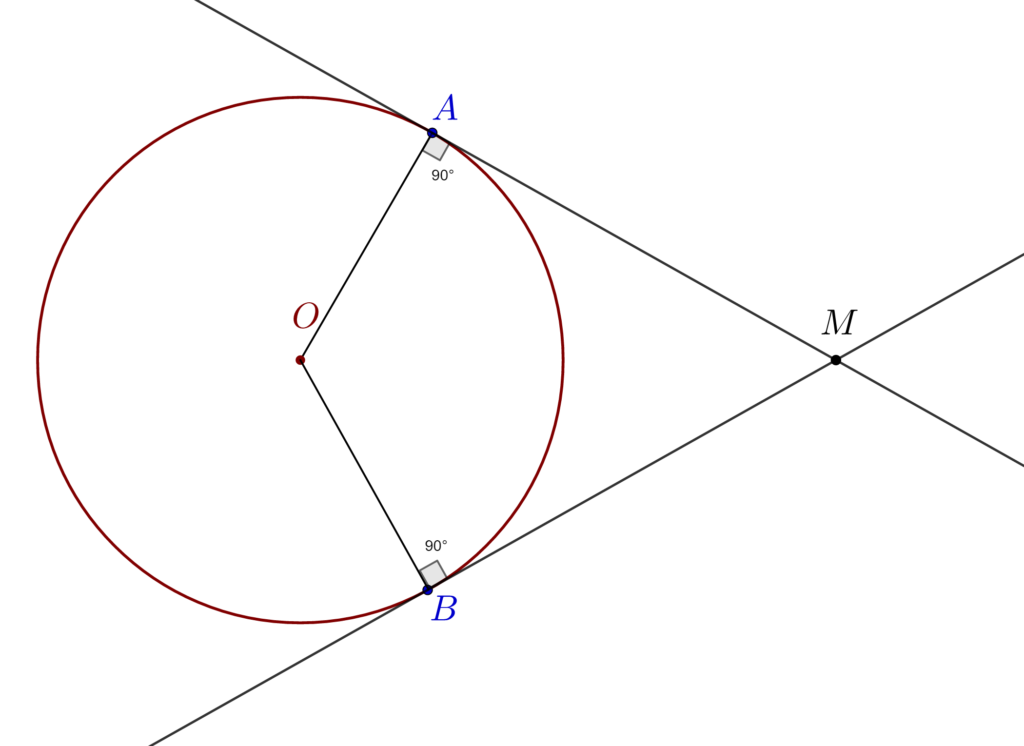
- Tangenta la cerc este dreapta care intersectează cercul într-un punct.
Tangenta este perpendiculară pe raza cercului dusă în punctul de tangență. Dintr-un punct exterior unui cerc se pot duce două drepte tangente.
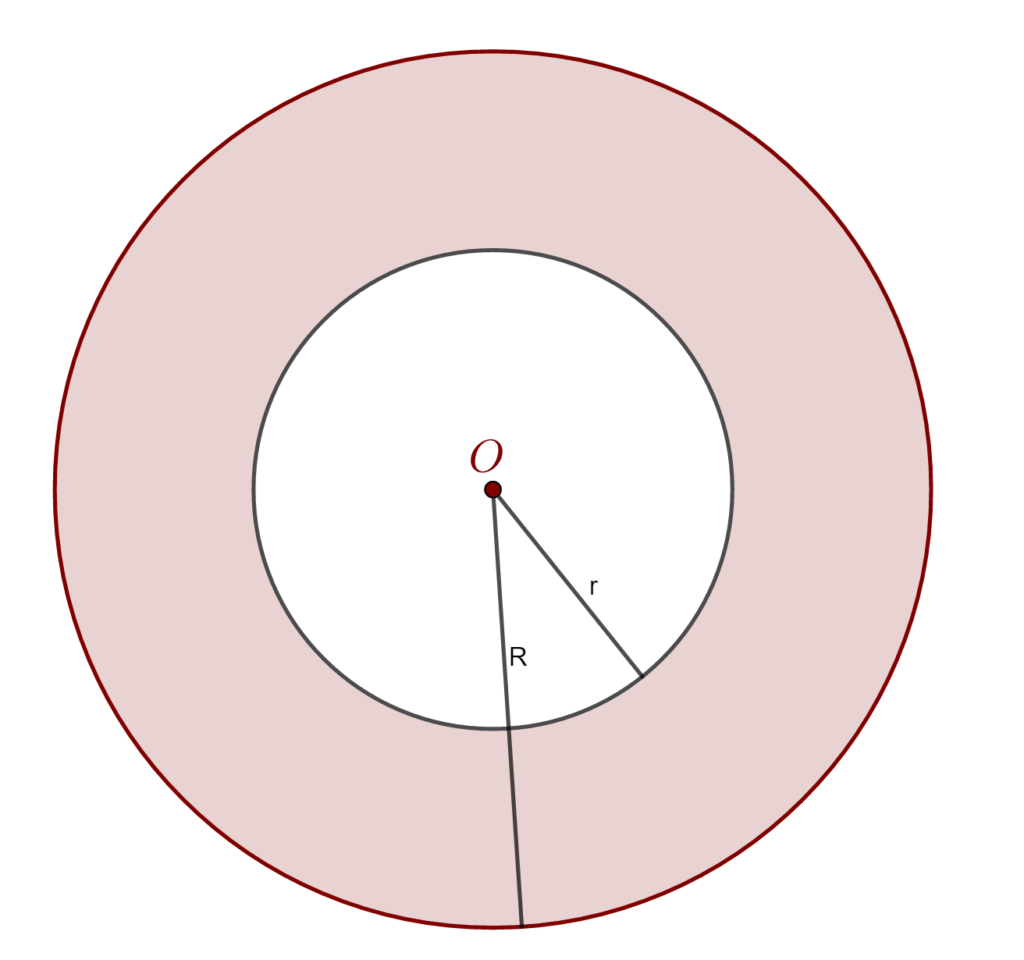
- O coroană circulară este porțiunea plană cuprinsă între două cercuri concentrice de raze diferite: R și r.
Notații și formule
Vom nota cu R lungimea razei cercului, cu L lungimea (circumferința) cercului și cu S aria cercului (de fapt a discului).
Vom nota cu π raportul dintre circumferința și diametrul oricărui cerc. Numărul π este o constantă matematică a cărei valoare este egală cu aproximativ 3,14159.
Lungimea cercului:
L = 2\pi R \\\;\\
Aria cercului (discului):
S=\pi R^2
Lungimea arcului AB este:

l_{arc}=R\cdot m(\measuredangle AOB)\; \\\;\\pentru \;\measuredangle AOB\;măsurat\;în \; radiani \\\;\\sau\\\;\\
l_{arc}=\frac{\pi \cdot R\cdot m(\measuredangle AOB)}{180^\circ }\; \\\;\\pentru \;\measuredangle AOB\;măsurat\;în \; gradeAria sectorului AOB este:

A_{ \;sectorului\;AOB }=\\\;\\=\frac{m(\measuredangle AOB) \cdot R^2}{2}\\\;\\pentru \;\measuredangle AOB\;măsurat\;în \; radiani \\\;\\sau\\\;\\A_{ \;sectorului\;AOB }=\\\;\\=\frac{\pi \cdot R^2 \cdot m(\measuredangle AOB)}{360^\circ}\\\;\\pentru\;\measuredangle AOB\;măsurat\;în \; gradeAria segmentului de cerc:

A_{\;segmentului\;AB}= \\\;\\
= A_{ \;sectorului\;AOB} -A_{ △ AOB}Aici vă vor fi de ajutor și formulele pentru calculul ariei unui triunghi.
Aria coroanei circulare este dată de formula de mai jos:

A_{coroanei\;circulare}\;=\\=\pi\cdot(R^2-r^2)Unghiuri raportate la un cerc:
Unghiul la centru este un unghi cu vârful în centrul cercului, O. Măsura acestuia este egală cu măsura arcului subîntins de laturi.
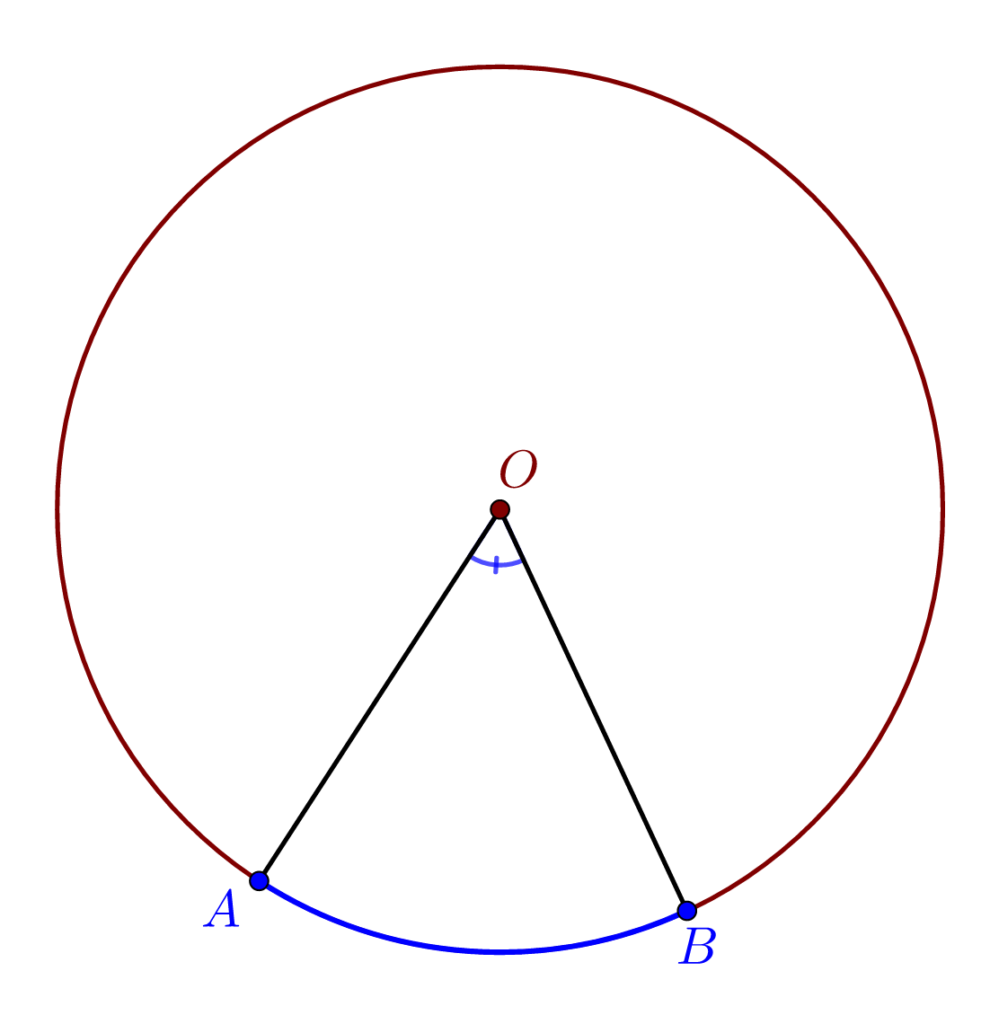
m(\measuredangle AOB) =m(\overset{\frown}{AB})Unghiul înscris în cerc este un unghi cu vârful pe cerc. Măsura sa este egală cu jumătatea măsurii arcului subîntins de laturi.
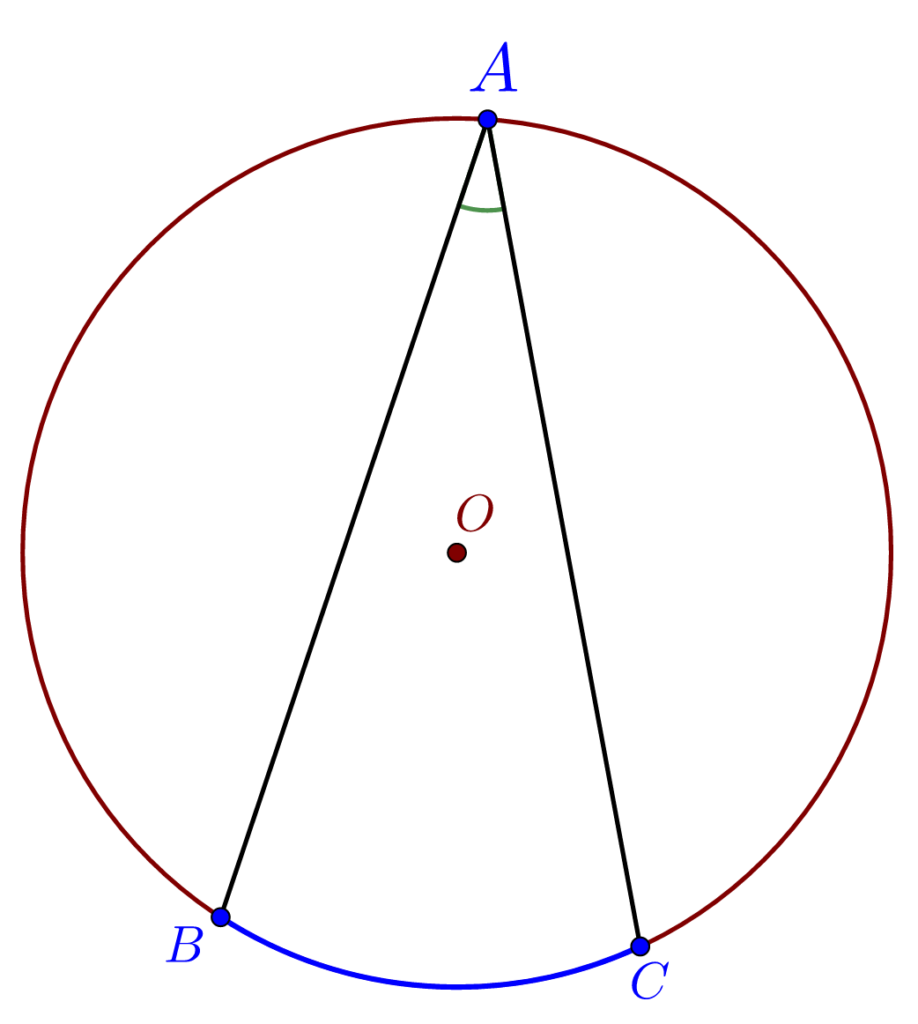
m(\measuredangle BAC) = \frac{m(\overset{\frown}{BC})}{2}Consecințe:
-1) un unghi înscris într-un semicerc are măsura de 900, sau π/2 . (o teoremă a lui Thales)
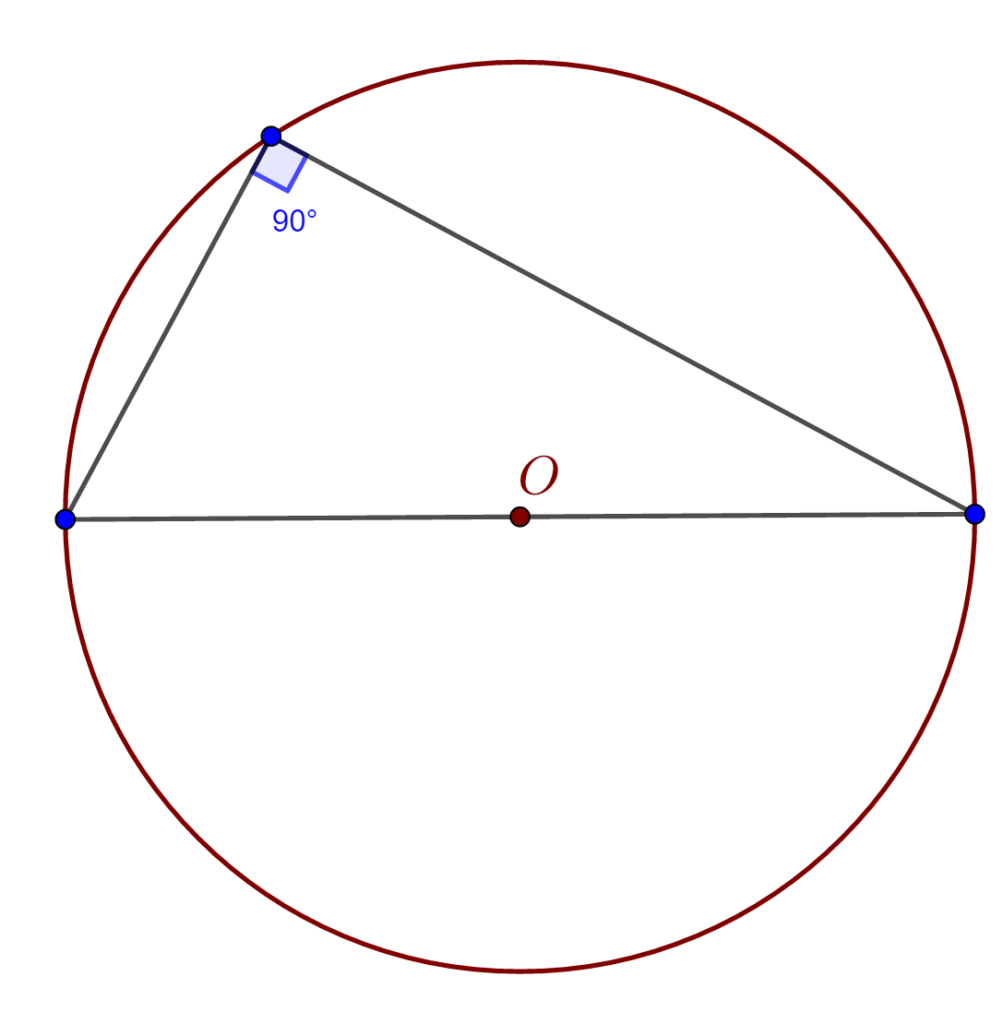
-2) două unghiuri înscrise în același cerc și care subîntind același arc sunt unghiuri congruente.
Măsura unghiului cu vârful în interior este egală cu semisuma arcelor determinate pe cerc de către laturile sale.
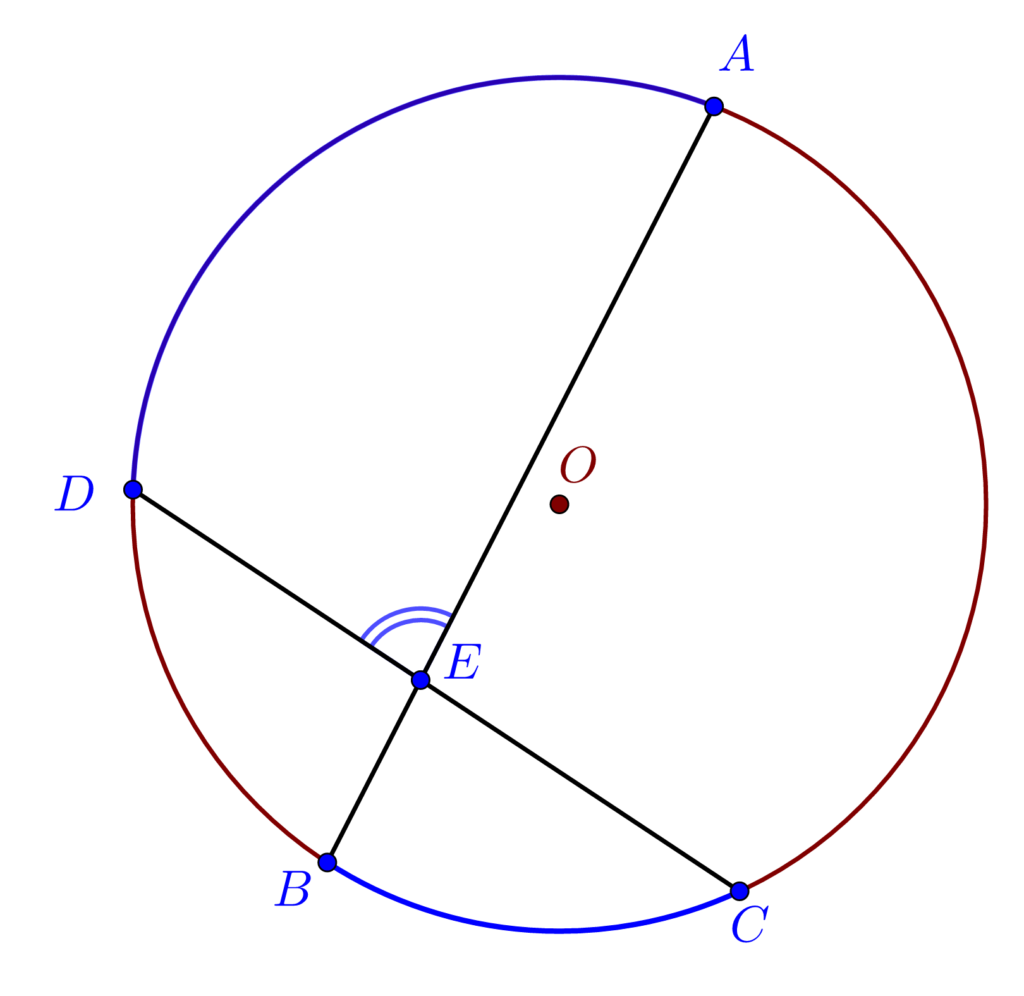
m(\measuredangle AED) = \frac{m(\overset{\frown}{AD})+m(\overset{\frown}{BC})}{2}Măsura unghiului cu vârful în exteriorul cercului este egală cu semidiferența arcelor determinate pe cerc de către laturile sale.
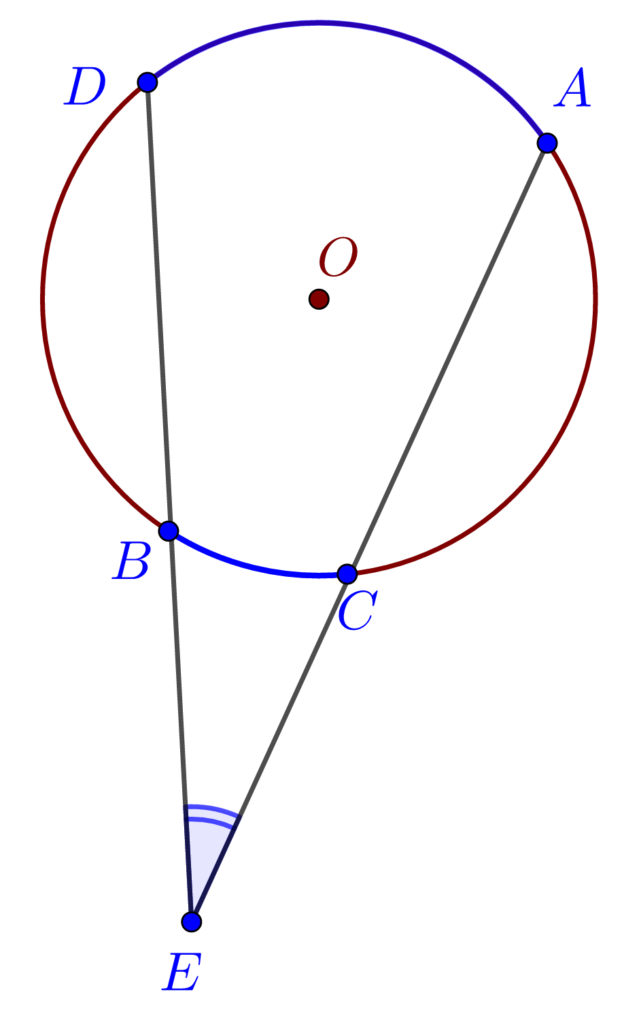
m(\measuredangle AED) = \frac{m(\overset{\frown}{AD})-m(\overset{\frown}{BC})}{2}
Teoreme:
1). În același cerc sau cercuri egale, la unghiuri la centru egale corespund arce și coarde egale și reciproc.
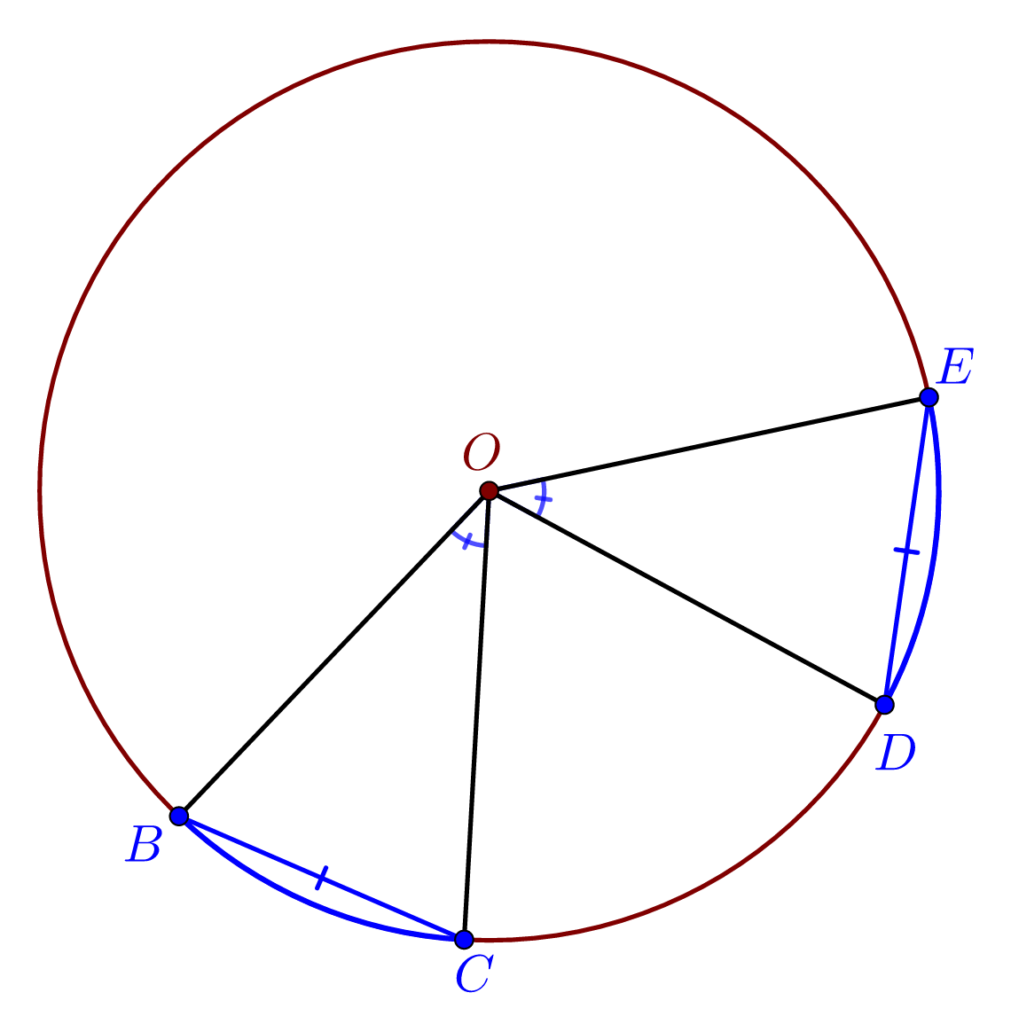
2). În același cerc sau cercuri egale, la arce egale corespund coarde egale și reciproc.
3). Diametrul perpendicular pe o coardă a cercului împarte coarda și arcele corespunzătoare în două părți egale și reciproc.
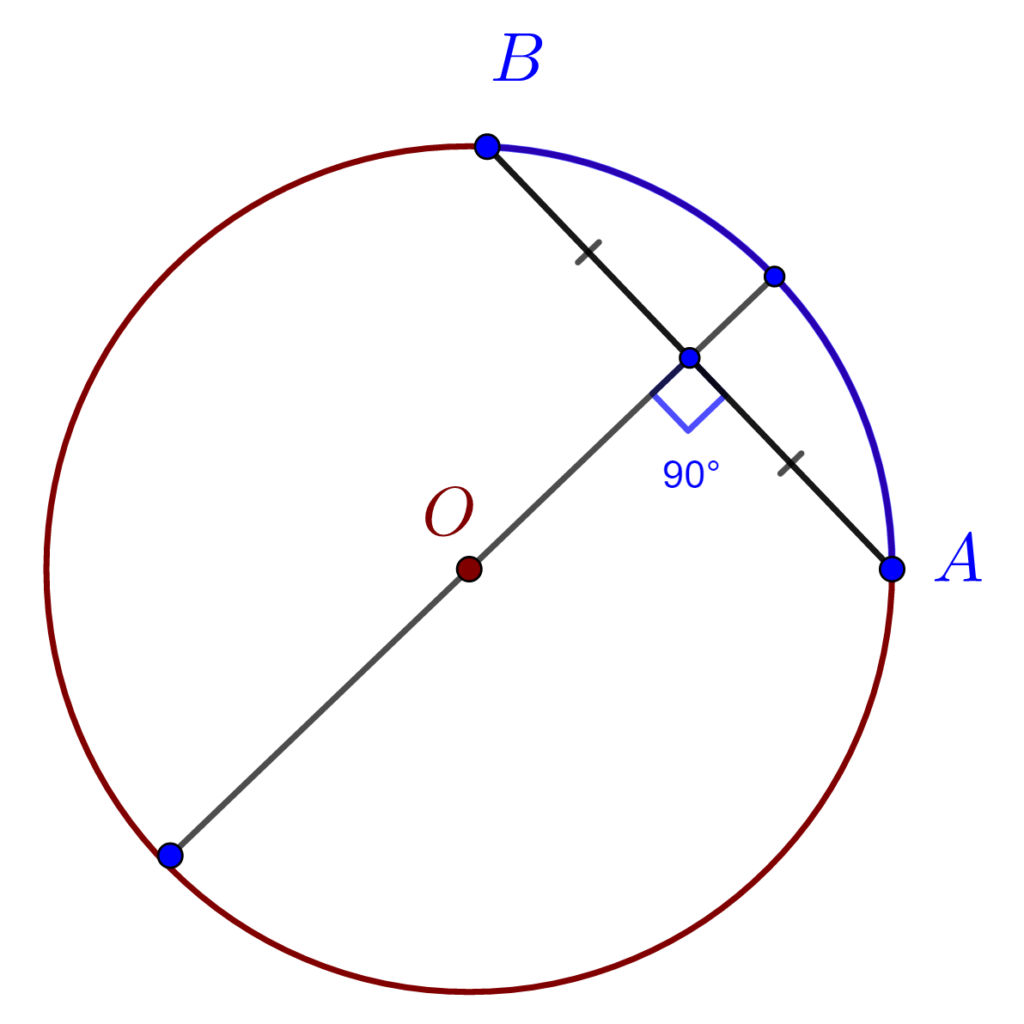
4). Arcele cuprinse între două coarde paralele sunt egale.
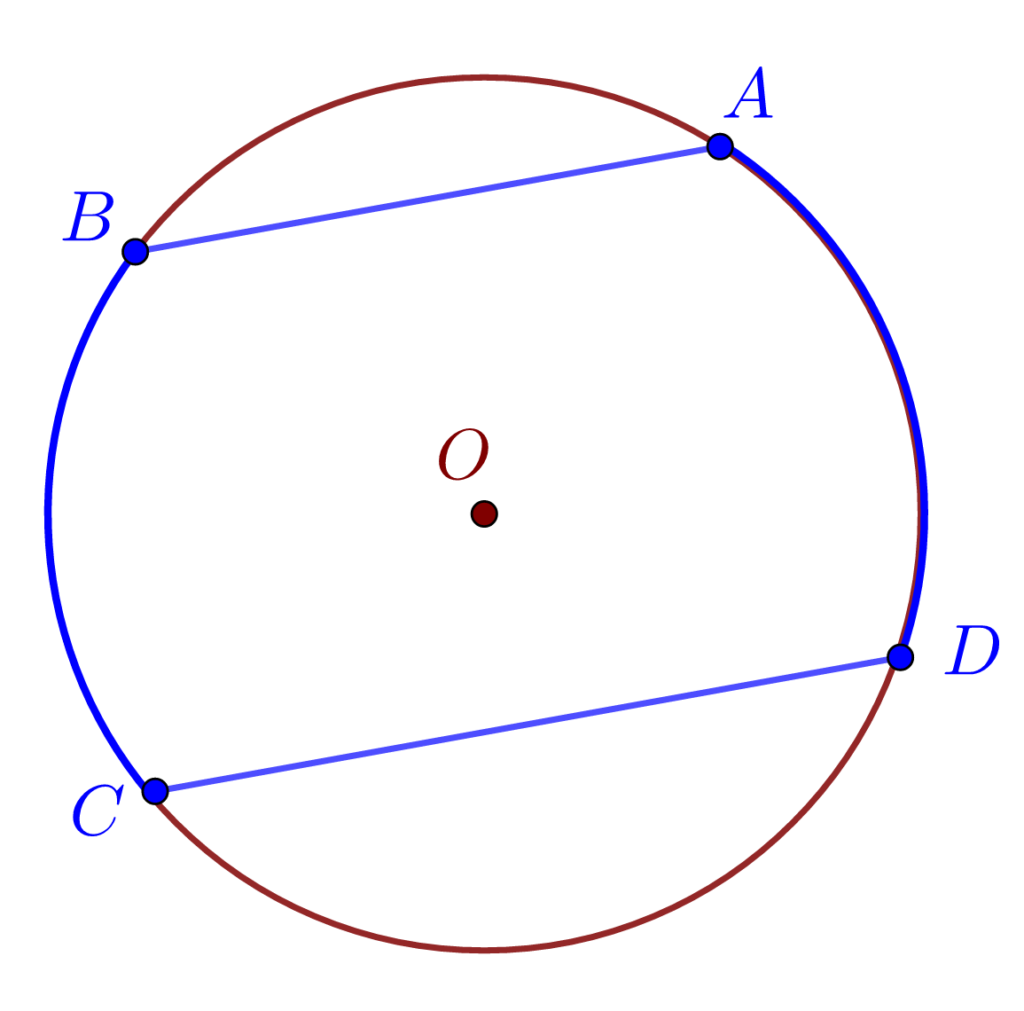
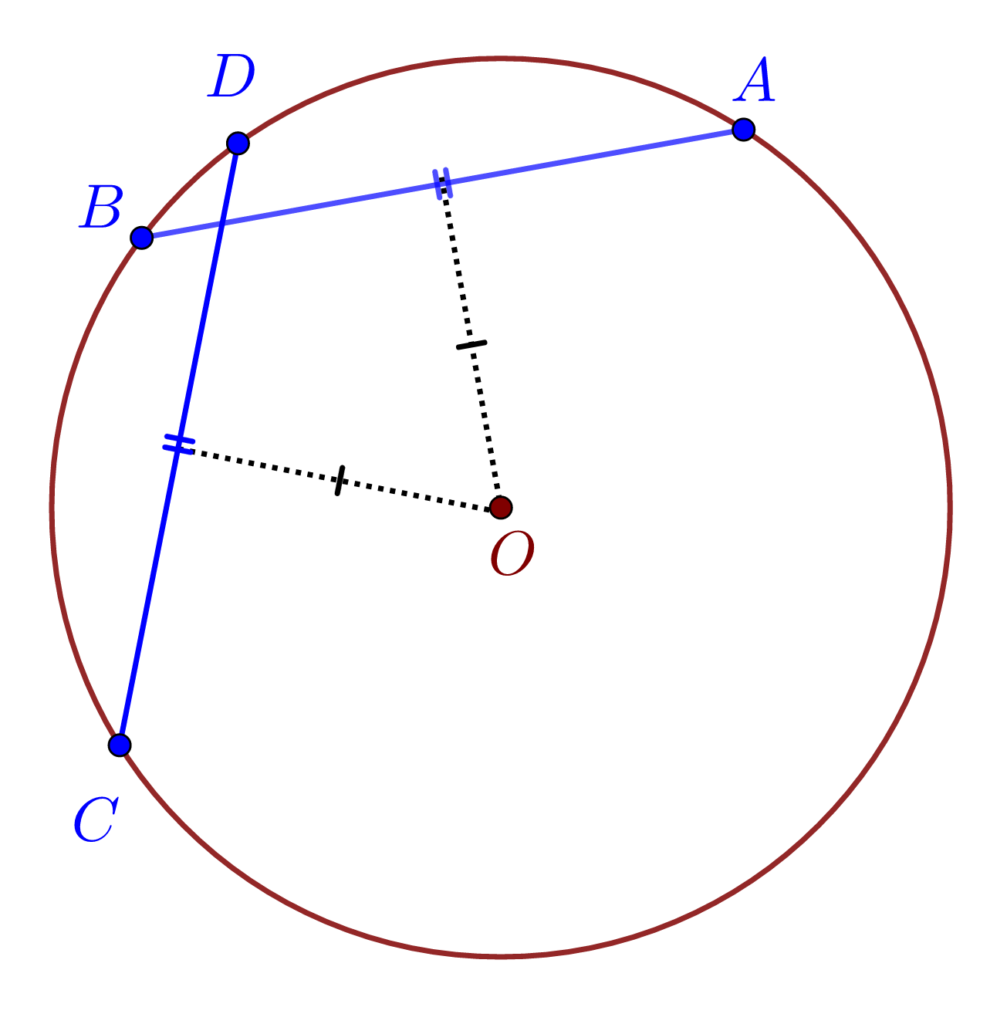
5). În același cerc sau în cercuri egale, coardele egale sunt egal depărtate de centru și reciproc.
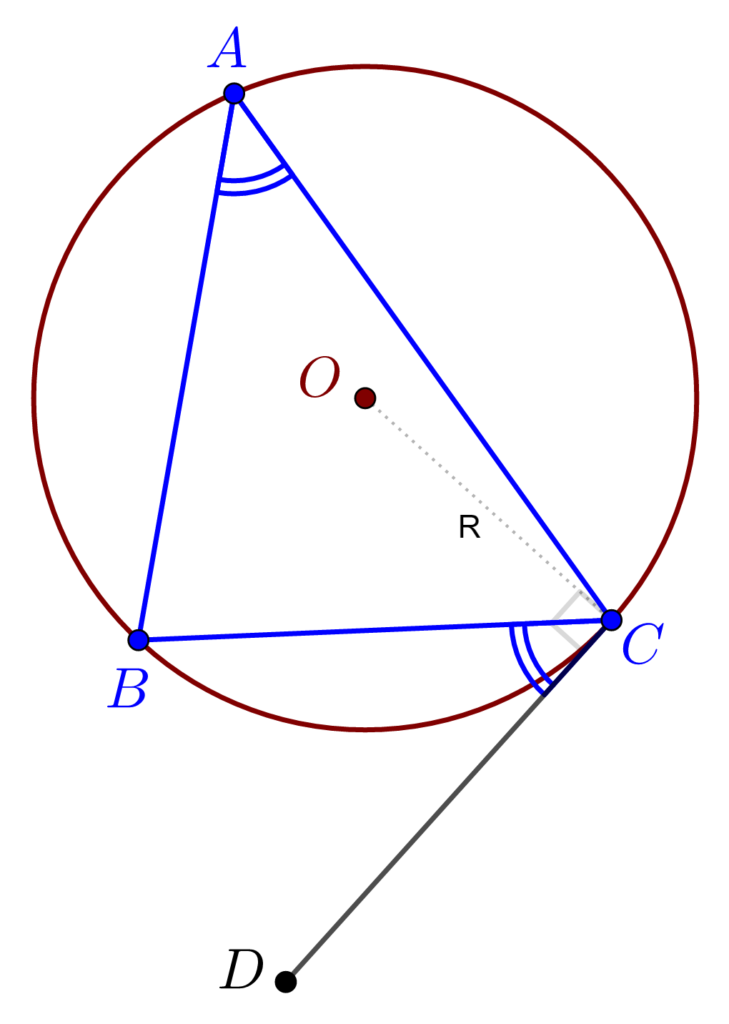
6). Dacă ABC este un triunghi înscris într-un cerc si CD este o semitangentă în C, atunci măsura unghiului CAB este egala cu măsura unghiului DCB.
7). Teorema ciocului de cioară – Fie un punct exterior unui cerc, dacă ducem tangentele la cerc din acest punct atunci lungimile segmentelor formate de punctul exterior și punctele de tangență sunt egale (MA=MB).




