Triunghiul oarecare – cele mai importante 16 teoreme

Cele 16 teoreme descrise mai jos ne ajută în rezolvarea și înțelegerea multor probleme despre triunghiul oarecare, dar mai întâi să vedem care sunt liniile importante în triunghi.

Liniile importante in triunghi:

Fie triunghiului oarecare ABC: notăm cu a lungimea laturii opuse unghiului A, cu b lungimea laturii opuse unghiurilor B si cu c lungimea laturii opuse unghiului C; notăm cu m_a lungimea medianei ce pleacă din vârful A, notăm cu i_a lungimea bisectoarei ce pleacă din vârful A. Notăm cu p semiperimetrul triunghiului ABC, p = (a+b+c)/2. Notăm cu S aria triunghiului ABC.

1. Bisectoarea

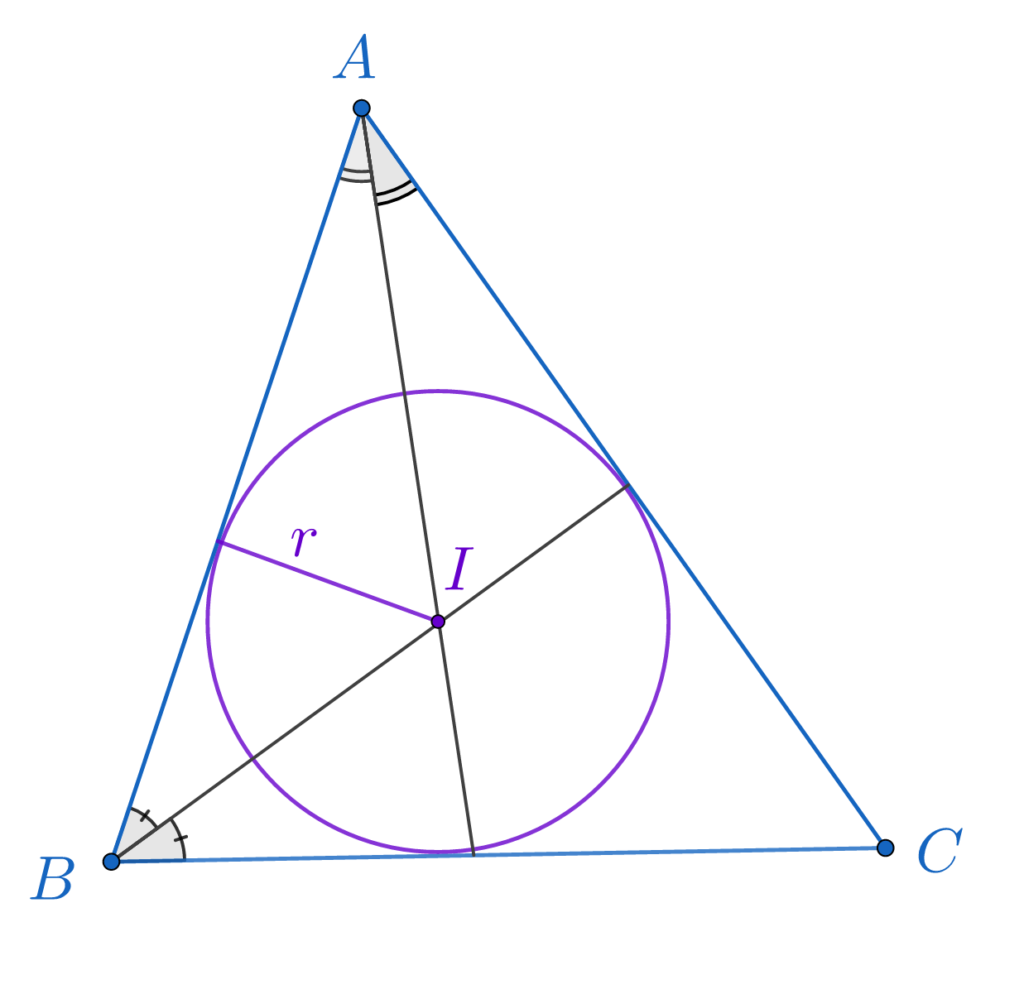
Bisectoarea unui unghi este locul geometric al punctelor interioare unui unghi egal departate de laturile sale, sau semidreapta cu originea în vârful unghiului, care împarte acest unghi în alte două unghiuri de măsuri egale.

Bisectoarele unghiurilor unui triunghi sunt concurente in centrul cercului înscris în triunghi notat I, cu raza r.

Raza cercului înscris este egală cu raportul dintre aria triunghiului si semiperimetrul acestuia:

r = \frac{S}p

Lungimea bisectoarei unui unghi este dată de următoarele relații:

i_a= \frac{2}{(b+c)}\cdot \sqrt[]{pbc\cdot(p-a)} \;\\\;\\\;unde\;\;p = \frac{a +b+c}{2}\;\;\;\;\;\;\;\;\;\;

i_a^2= bc -\frac{a^2bc}{(b+c)^2} \\ \;\\sau \\\;\\i_a^2= \frac{bc}{(b+c)^2} \cdot((b+c)^2 -a^2)

i_a=\frac{2bc\cdot cos\frac{A}{2}}{b+c}

La fel se pot calcula și lungimile bisectoarelor corespunzătoare celorlate unghiuri ale triunghiului.

2. Mediatoarea

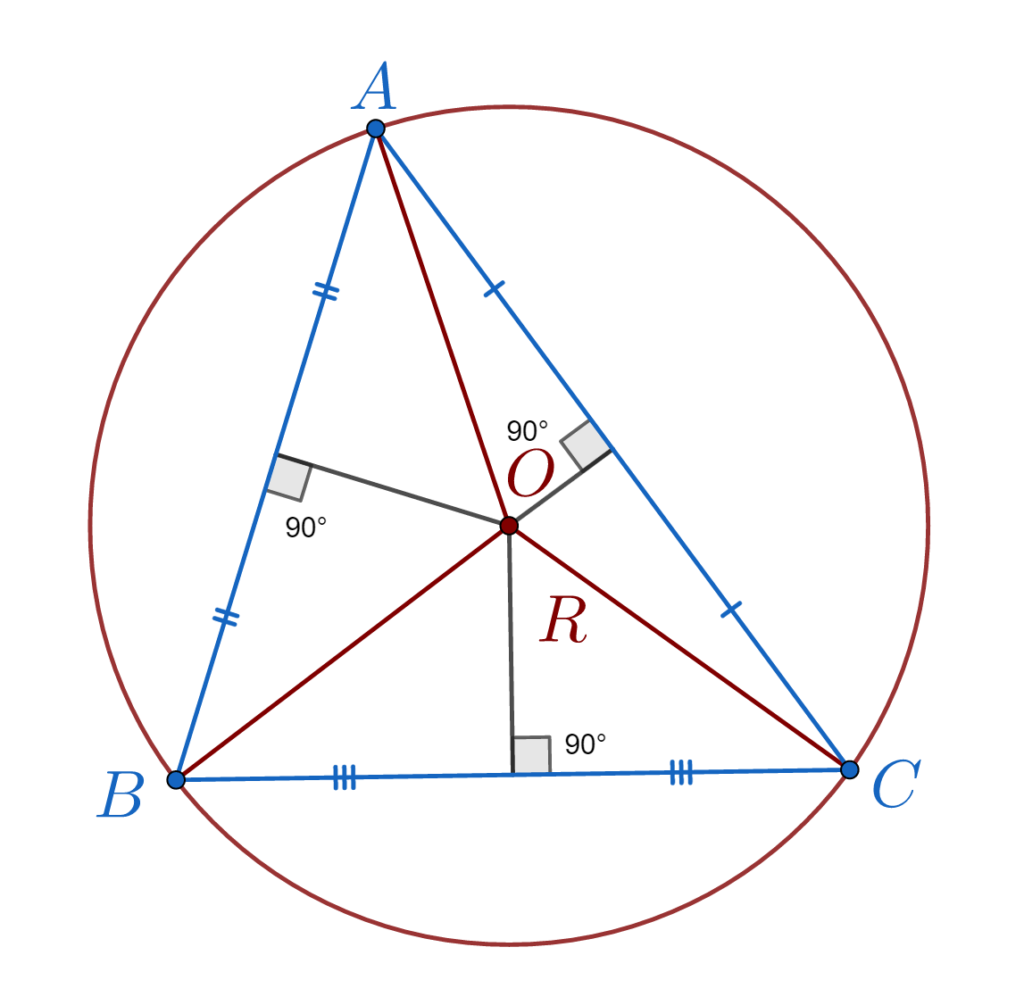
Mediatoarea este locul geometric al punctelor din plan egal depărtate de extremintațile segmentului, sau altfel spus perpendiculara dusă prin mijlocul unui segment.

[the_ad_group id=”104″]

Mediatoarele laturilor unui triunghi sunt concurente în centrul cercului circumscris triunghiului notat O cu raza R.

Teorema sinusurilor – este o relație de proporționalitate între lungimile laturilor unui triunghi și sinusurile unghiurilor respective opuse. Aceasta permite, cunoscând două unghiuri și o latură, să se calculeze lungimea celorlalte laturi.

\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2 R

R=\frac{abc}{4\cdot S}

Gasiți aici 10 formule pentru a calcula aria unui triunghi oarecare.

Articolul continuă pe pagina următoare