Aria triunghiului dreptunghic și alte formule de bază

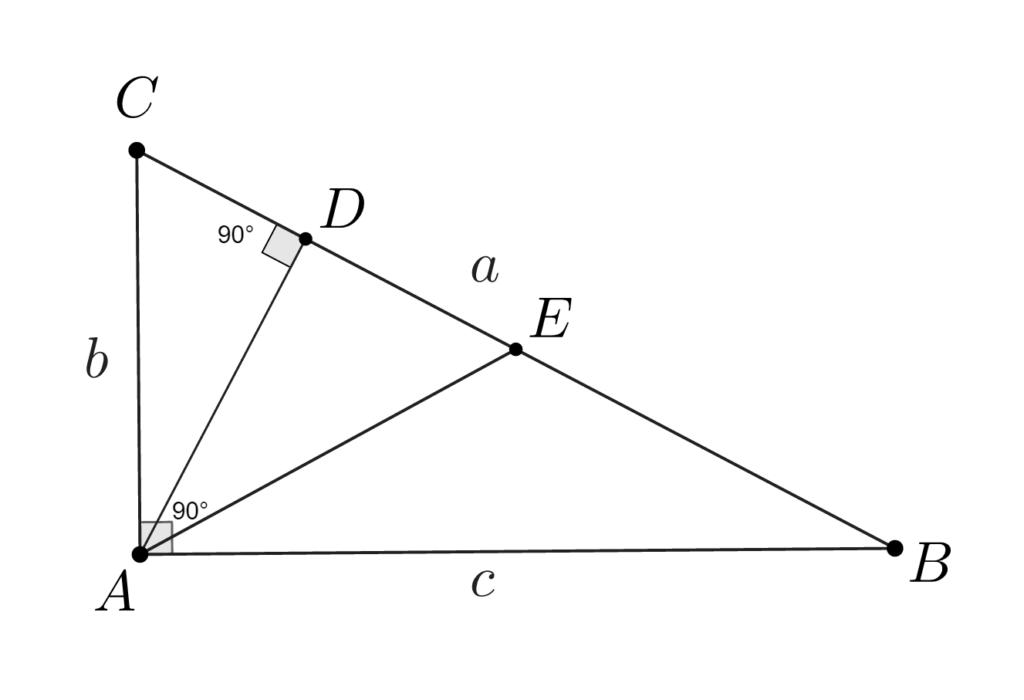
Fie triunghiul dreptunghic ABC cu măsura unghiului A de 90^o. Latura opusă unghiului de 90^o , BC, se numește ipotenuză. AB și AC se numesc catete. Notăm cu a lungimea ipotenuzei iar cu b și c lungimile catetelor opuse unghiurilor B respectiv C. Vezi mai jos două metode de a calcula aria triunghiului dreptunghic.

Construim înălțimea AD și mediana AE. Notăm cu R – raza cercului circumscris triunghiului ABC, r -raza cercului înscris triunghiului ABC și cu S – aria triunghiului dreptunghic ABC.

Teorema Pitagora

a^2=b^2+c^2

Pătratul ipotenuzei este egal cu suma pătratelor catetelor.

Teorema înălțimii

AD^2=CD\cdot DB

Pătratul înălțimii este egal cu produsul proiecțiilor catetelor pe ipotenuză.

Teorema catetei

AB^2=BD\cdot BC \\\;\\AC^2=CD\cdot BC

Pătratul catetei este egal cu produsul dintre proiecția catetei pe ipotenuză și ipotenuză.

[the_ad_group id=”104″]

Mediana AE

AE =  \frac{BC}{2} \; \\\;\\ AE = CE=BE

Mediana care pleacă din vârful de 90^o este jumătate din ipotenuză.

Cateta opusă unghiului de 30^o

Cateta opusă unghiului de 30^o este jumătate din ipotenuză.

Aria triunghiului dreptunghic folosind înălțimea din A

\;\;S = \frac{AD\cdot BC}{2} \; \\\;\\ 

Aria triunghiului dreptunghic este jumătatea produsului ipotenuzei și înălțimii din unghiul drept.

Aria triunghiului dreptunghic folosind relația dintre catete

S =  \frac{AC\cdot AB}{2} 

În triunghiul dreptunghic, aria este totodată egală cu jumătatea produsului dintre catete.

Articolul continuă pe pagina următoare