Teorema lui Thales

Imaginați-vă că trebuie să măsurați înălțimea celei mai mari piramide din Egipt – piramida lui Khufu (sau Cheops). Suntem însă în secolul VI î.Hr, cu peste 2500 de ani în urmă, și nu aveți la dispoziție tehnologia din ziua de azi – GPS, laser, sateliți… Legenda spune că Thales din Milet, unul dintre cei șapte înțelepți ai Greciei antice, a fost cel care a reușit să facă pentru prima dată acest lucru, folosindu-se de ceea ce noi azi cunoaștem drept teorema lui Thales.

Ce-i drept, fiind cum spuneam unul dintre cei șapte înțelepți, ne putem aștepta la o contribuție substanțială din partea lui Thales la înțelegerea lumii în care trăim. Există de fapt mai multe teoreme care îi sunt atribuite. În acest articol ne vom concentra pe cea referitoare la triunghiuri asemenea și segmente proporționale. O altă teoremă care îi poartă numele se referă la măsura unui unghi înscris într-un semicerc.

Ce spune teorema lui Thales?

Într-un triunghi ABC ducem o dreaptă paralelă cu o latură, să zicem cu BC, care intersectează celelalte laturi în D, respectiv E. Atunci, raportul dintre AD și DB este egal cu raportul dintre AE și EC. De exemplu, dacă dreapta paralelă cu BC intersectează AB la jumătate, atunci va intersecta AC tot la jumătate.

Formal, teorema lui Thales s-ar enunța așa:

\begin{rcases}\Delta ABC\\ D\in AB, E\in AC\\ DE||BC\end{rcases} \implies\frac{AD}{DB}=\frac{AE}{EC}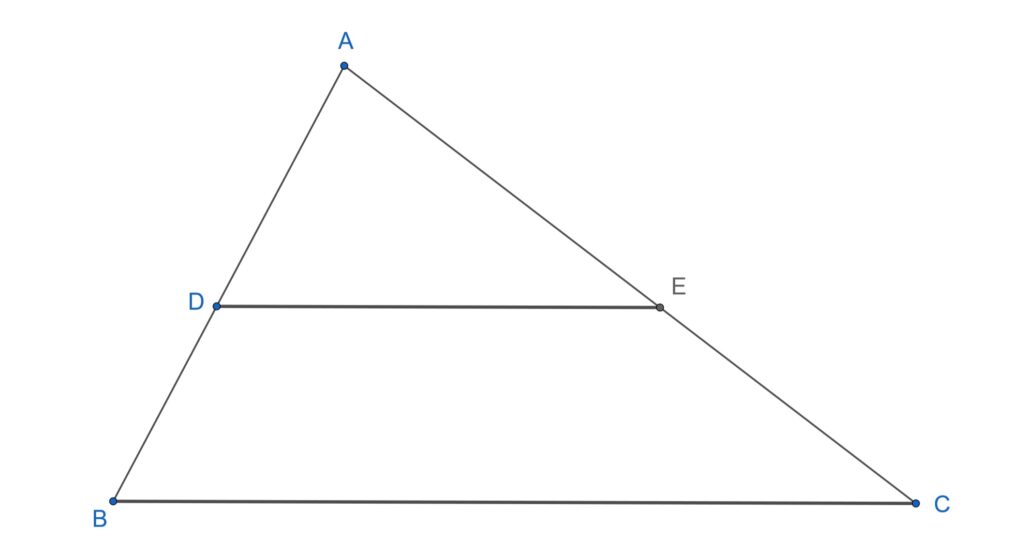

Teorema apare în Elementele lui Euclid (cartea VI, propoziția 2), o lucrare ce datează din perioada anilor 300 î.Hr., cu aproape trei sute de ani mai târziu decât perioada în care a trăit Thales, și care stă la baza geometriei (surpriză!) euclidiene.

Demonstrația lui Euclid

Euclid propune următoarea demonstrație pentru teorema lui Thales. Începe prin a trasa segmentele CD și BE, ca în figura de mai jos.

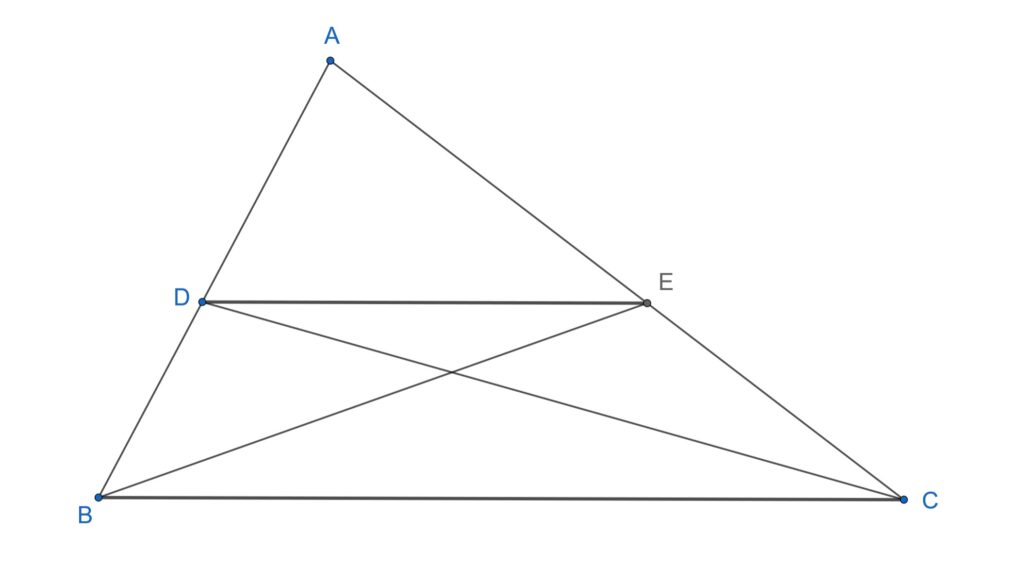
Demonstrația sa se bazează pe faptul că ariile triunghiurilor BDE și CDE sunt egale. De ce? Încercați să găsiți singuri răspunsul la această întrebare. Să zicem doar că Euclid demonstrează în altă parte (carte I, prop. 37) că ariile triunghiurilor cu aceeași bază și vârfurile opuse pe o dreaptă paralelă cu această bază sunt egale. Mai mult, raportul dintre aria triunghiului ADE și aria triunghiului BDE este egal cu raportul dintre AD și DB.

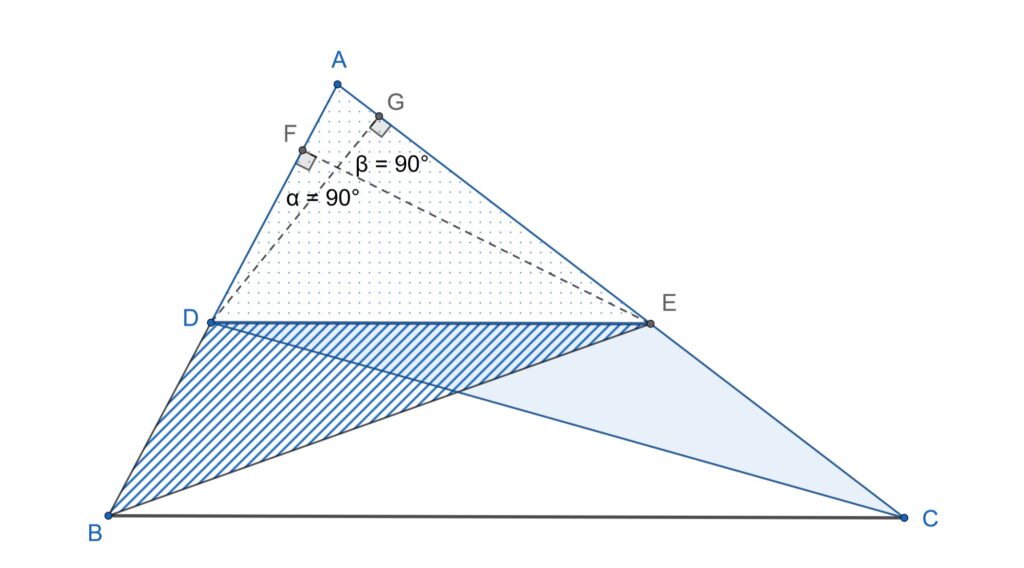
\begin{align}A_{\Delta BDE} &= A_{\Delta CDE}\,\\[1em]
\begin{rcases}
A_{\Delta BDE} = \frac{DB\cdot EF}{2}\\[1em]
A_{\Delta ADE} = \frac{AD\cdot EF}{2}
\end{rcases}&\implies \frac{A_{\Delta ADE}}{A_{\Delta BDE}} = \frac{AD}{DB}\\[1em]

\begin{rcases}
A_{\Delta CDE} = \frac{EC\cdot DG}{2}\\[1em]
A_{\Delta ADE} = \frac{AE\cdot DG}{2}
\end{rcases} &\implies \frac{A_{\Delta ADE}}{A_{\Delta CDE}} = \frac{AE}{EC}\\[1em]
(1),(2),(3)&\implies\frac{AD}{DB}=\frac{AE}{EC} (q.e.d)
\end{align}

Folosindu-ne de proprietățile rapoartelor egale, putem deduce mai departe:

\begin{align*}
\frac{AD}{AD + DB} = \frac{AE}{AE+EC}\implies\frac{AD}{AB}=\frac{AE}{AC}
\end{align*}

Aș vrea să obțin și informații despre raportul între DE și BC. Bine, ADE și ABC fiind triunghiuri asemenea, știm dinainte că laturile sunt proporționale două câte două. Dar cum putem ajunge la acest rezultat plecând de la teorema lui Thales?

Ducem segmentul HE paralel cu AB.

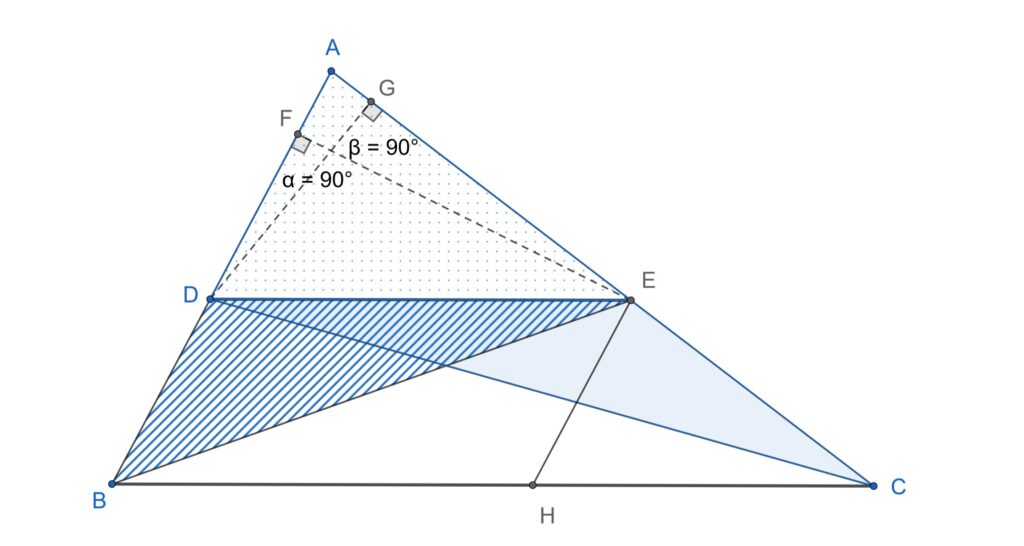
\begin{align*}
&\begin{rcases}
\begin{align*}
HE||AB \overset{Thales}{\implies}\frac{CH}{BH}=\frac{CE}{AE}&\\[1em]
BH\equiv DE
\end{align*}
\end{rcases}\iff\\[1em]
&{\iff}\frac{CH}{DE}=\frac{CE}{AE}{\iff}\\[1em]
&{\iff}\frac{BC-DE}{DE}=\frac{CE}{AE}{\iff}\\[1em]
&{\iff}\frac{BC}{DE}-1=\frac{CE}{AE}{\iff}\\[1em]
&{\iff}\frac{BC}{DE}=1+\frac{CE}{AE}{\iff}\\[1em]
&{\iff}\frac{BC}{DE}=\frac{AC}{AE}\iff\\[1em]
&{\iff}\frac{DE}{BC}=\frac{AE}{AC}
\end{align*}

În concluzie:

\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}

Reciproca la teorema lui Thales – este ea adevărată?

Reciproca teoremei lui Thales este de asemenea adevărată. Dacă o dreaptă împarte două din laturile unui triunghi în segmente proporționale, atunci este paralelă cu cea de-a treia latură. Poți demonstra asta plecând de la egalitatea rapoartelor și ajungând la egalitatea ariilor triunghiurilor BDE și CDE. Cum baza DE este comună, rezultă că înălțimile din B și respectiv din C sunt egale. Deci DE și BC sunt paralele.

Aplicații practice pentru teorema lui Thales

Măsurarea înălțimii obiectelor

Să revenim la problema inițială, cea a măsurării înălțimii piramidei lui Khufu. Pentru Thales și oamenii contemporani lui, Marea Piramida din Giza era deja un monument străvechi, o sursă de uimire și de admirație pentru civilizația egipteană. În acele timpuri, piramida exista deja de vreo două mii de ani. Comparativ, pentru noi un monument cu o vechime similara ar fi fost construit pe la începuturile erei noastre, pe când Marea Mediterană era un mare “lac” al Imperiului Roman.

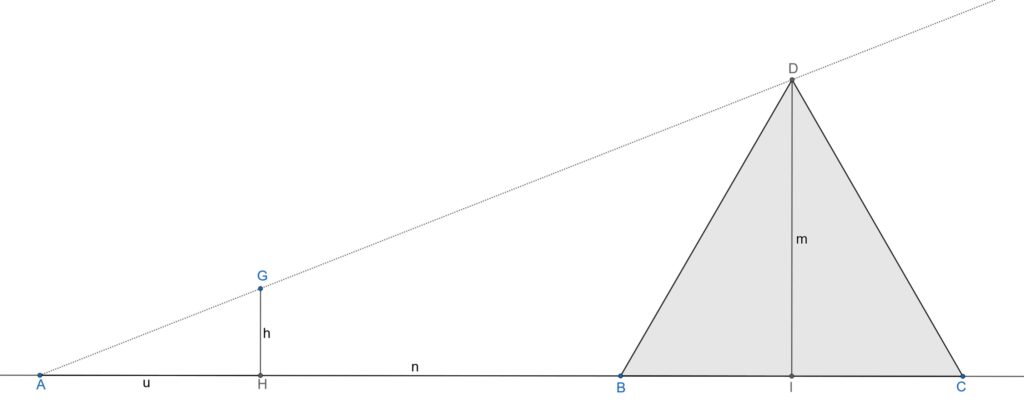
În imaginea de mai sus avem o reprezentare schematică a problemei. Am notat următoarele:

• D – vârful piramidei
• BC – baza piramidei
• I – proiecția vârfului pe BC
• H – un punct unde am plasat un obiect de înălțime cunoscută h, asftel încât umbra sa să se termine în același loc cu umbra piramidei (nu încercați acest experiment noaptea!).
• A – punctul unde se termină atât umbra piramidei cât și a obiectului.
• u – lungimea umbrei obiectului, adică distanța dintre H și A
• n – distanța dintre A și I. În principiu, măsurătorile de la sol ar fi putut fi accesibile lui Thales chiar și în epoca respectivă.
• m – înălțimea piramidei, ceea ce trebuie calculat.

Atunci, conform cu observațiile de mai sus, derivate din teorema lui Thales, avem următoarea relație:

\frac{u}{n} = \frac{h}{m}\implies m=\frac{n\cdot h}{u}

Măsurarea distanțelor până la obiecte îndepărtate

Vedem o navă inamică la orizont și vrem să știm cam în cât timp ajunge la țărm. Se spune că Thales a inventat o metodă de a calcula distanța de la mal până la o corabie. Secolul VI î.Hr. – cum spuneam, nu existau radarul, laserul sau GPS-ul, ca în zilele noastre.

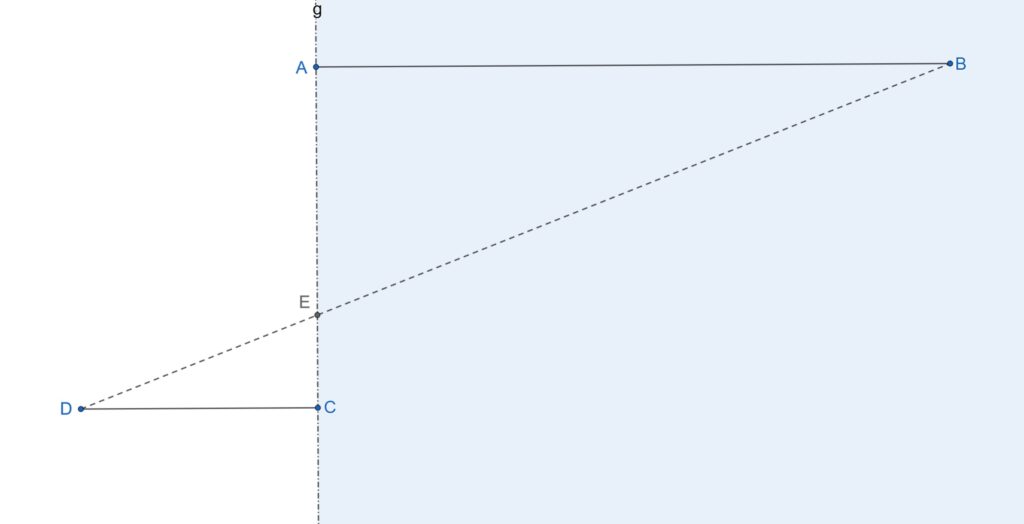
În imaginea de mai sus:

• B este poziția corabiei
• g este linia țărmului
• A este punctul de pe țărm din dreptul corabiei
• C este alt punct de pe mal
• D este un punct ales pe mal astfel încât CD și AB să fie paralele
• E este un punctul unde DB intersectează linia țărmului g. Cum credeți că se poate determina poziția acestui punct pe mal?

În figura de mai sus sunt cunoscute AE, EC, CD și DE. Putem aplica teorema lui Thales (de fapt consecința ei, prezentată mai sus) pentru a determina lungimea segmentului AB, chiar dacă paralela CD este în afara triunghiului ABE. (De ce?)

\frac{CD}{AB}=\frac{CE}{AE}\implies AB=\frac{CD\cdot AE}{CE}

Importanța teoremei lui Thales

Ca mai toate conceptele de bază, pe lângă utilitatea practică în viața de zi cu zi, importanța teoremei trebuie privită și prin prisma conceptelor care depind de ea. De exemplu, folosind teorema lui Thales putem deduce, cum am făcut mai sus, rapoartele între laturile triunghiurilor asemenea. Apoi, acest lucru ne ajută în teorema înălțimii unui triunghi dreptunghic. Și așa mai departe. Aceste înlănțuiri logice au ajutat omenirea să înțeleagă și mai apoi să stăpânească mediul său natural.