Introducere:
Partea întreagă și partea fracționară a unui număr real constituie descompunerea acestuia în două părți distincte, facilitând atât studiul numerelor reale, cât și aplicarea lor eficientă într-o varietate de domenii. Această separare ajută la analiza detaliată a proprietăților numerelor reale și la optimizarea utilizării lor în contexte practice.
Definiții și fundamente:
Partea întreagă:
Partea întreagă sau partea întreagă inferioară, a unui număr real x este cel mai mare număr întreg (pozitiv, negativ sau nul) care este mai mic sau egal cu x .
Notația [x] pentru partea întreagă a fost introdusă de Carl Friedrich Gauss în 1808 și s-a menținut până în 1962 când au apărut noțiunile de parte întreagă inferioară echivalentă cu partea întreagă \lfloor x \rfloor și de parte întreagă superioară \lceil x \rceil introduse de Kenneth Iverson.
Ambele notații, [x] și \lfloor x \rfloor, sunt acum utilizate în matematică pentru partea întreagă denumită și partea întreagă inferioară. În acest articol vom folosi notația introdusă de Carl Friedrich Gauss și anume [ ].
Partea întreagă sau partea întreagă inferioară este definită astfel:
[x] \in \Z \\[1em] [x] \leq x < [x] +1
Deci putem spune că [x] este cel mai mare număr întreg care este mai mic sau egal x .
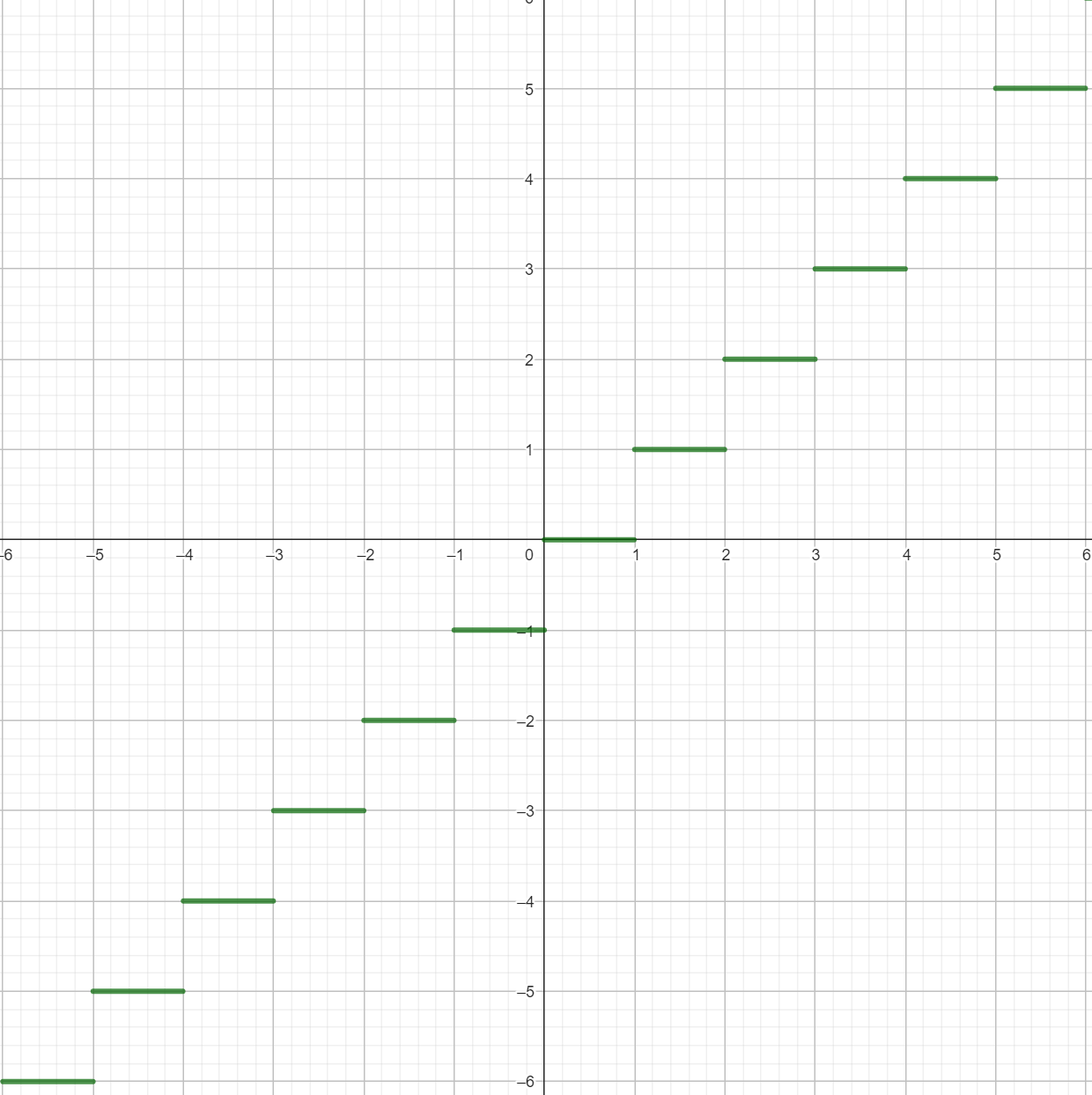
parte întreagă (inferioară)
Partea întreagă superioară este definită astfel:
\lceil x \rceil \in \Z \\[1em] \lceil x \rceil -1 < x \leq \lceil x \rceil
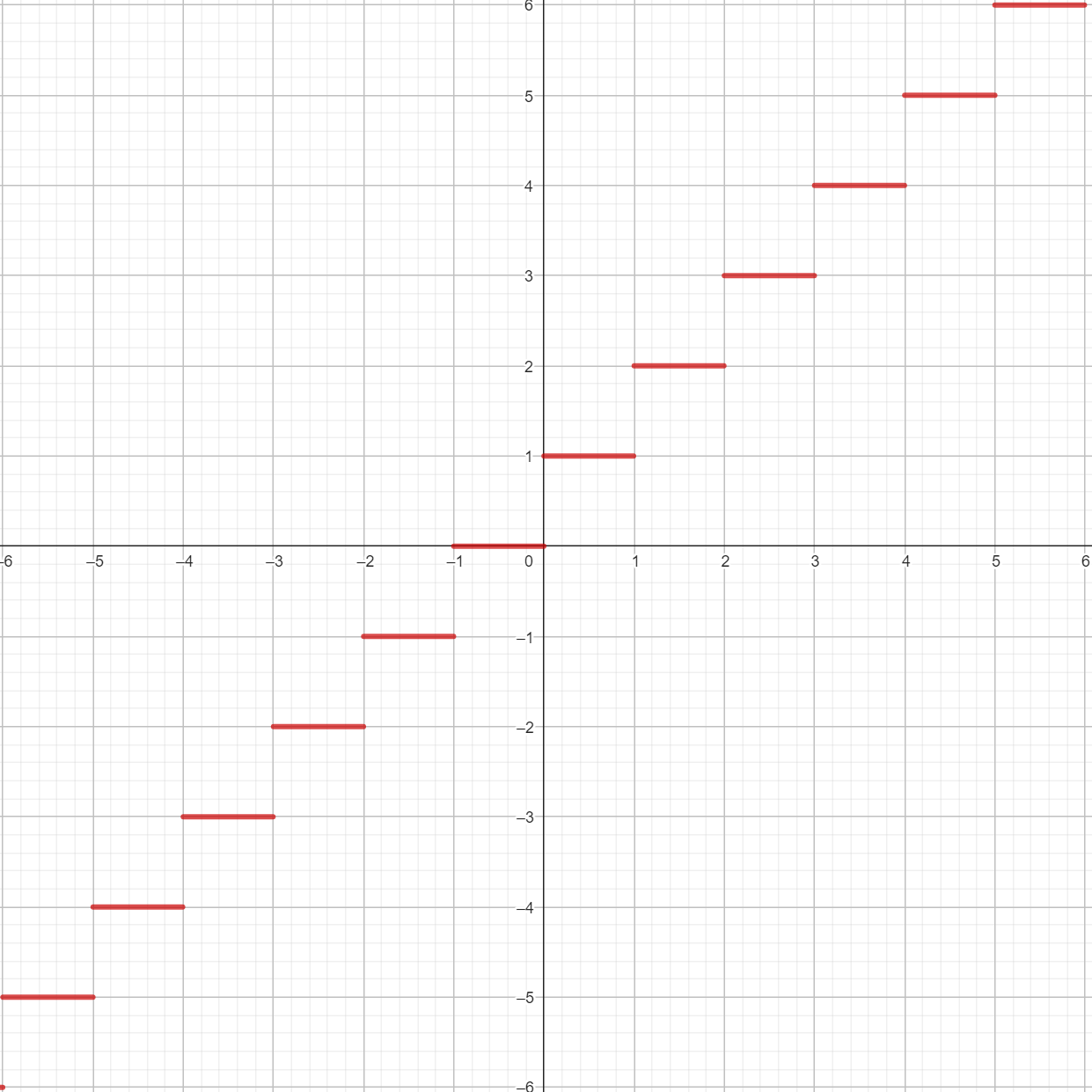
parte întreagă superioară
Existența părții întregi este garantată de principiul sau axioma lui Arhimede.
Atenție! Partea întreagă nu trebuie confundată cu trunchierea corespunzătoare eliminării zecimalelor deoarece în cazul numerelor negative aceasta este diferită de partea întreagă.
Partea fracționară:
Partea fracționară a unui număr real x este notată {x} și este diferența dintre acest număr și partea sa întreagă (partea întreagă inferioară):
\{x\} \in\R\\[1em]
\{x\} = x -[x]\\[1em]
0 \leq \{x\}<1
Deci partea fracționară a unui număr este un număr real pozitiv, mai mare sau egal cu zero, dar întotdeauna strict mai mic decât 1.
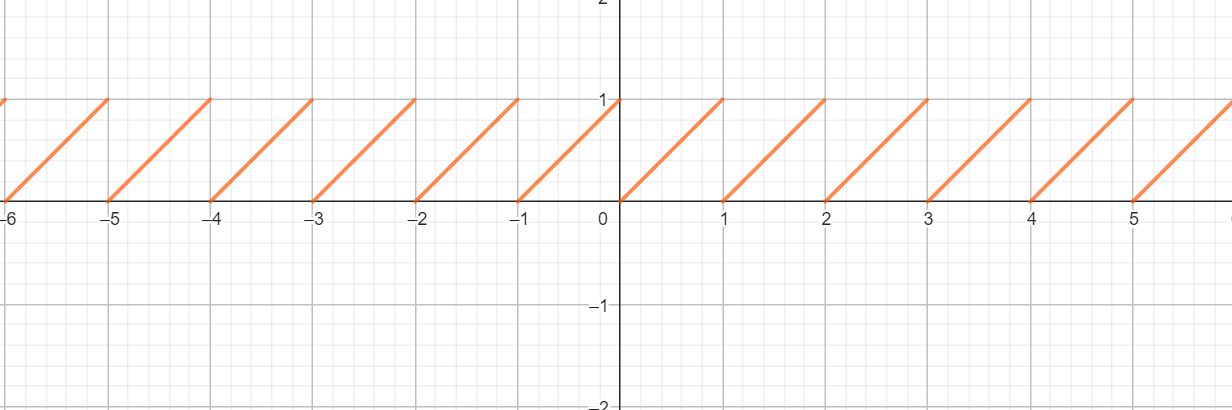
parte fracționară
Exemple pentru partea întreagă și partea fracționară
\begin{array}{|c|c|c|}
\hline
\text{numărul real } x & \text{partea întreagă } [x] & \text{partea fracționară } \{x\} \\
x & [x] \leq x < x+1 & \{x\} = x -[x] \\
\hline
-3.5 & -4 & 0.5 \\
\hline
3.5 & 3 & 0.5 \\
\hline
-2.1 & -3 & 0.9 \\
\hline
2.1 & 2 & 0.1 \\
\hline
-1 & -1 & 0 \\
\hline
0 & 0 & 0 \\
\hline
2 & 2 & 0 \\
\hline
3.7 & 3 & 0.7 \\
\hline
-3.7 & -4 & 0.3 \\
\hline
4.5 & 4 & 0.5 \\
\hline
5.9 & 5 & 0.9 \\
\hline
7 & 7 & 0 \\
\hline
8.3 & 8 & 0.3 \\
\hline
\end{array}
Tabelul de mai sus conține exemple de numere reale descompuse fiecare în partea sa întreagă (inferioară) și partea sa fracționară.
Reamintim că partea întreagă este cel mai mare întreg mai mic sau egal cu numărul folosit. Astfel, pentru numerele negative ca -2,1, valoarea părții întregi [-2,1] va fi -3. În cazul numerelor pozitive, ca 2,1, partea întreagă [2,1] este 2 iar procesul seamănă cu trunchierea, ceea ce nu se aplică numerelor negative.

De asemenea, apar diferențe în calculul părții fracționare, care este determinată ca diferența dintre numărul inițial și partea sa întreagă. În acest mod, partea fracționară a lui -2,1 este 0,9, calculată prin -2,1 – (-3), în timp ce pentru 2,1, partea fracționară este 0,1, rezultată din 2,1 – 2. Reamintim că partea fracționara este mereu mai mare sau egala cu 0, deci pozitivă, chiar și în cazul numerelor negative.
Proprietăți elementare pentru partea întreagă și partea fracționară
Pentru \forall x \in \R avem următoarele proprietăți:
- Partea întreagă a părții întregi a unui număr real este egală cu partea întreagă a acelui număr:
[[x]] = [x]
2. Partea fracționară a părții fracționare a unui număr real este egală cu partea fracționară a acelui număr:
\{\{x\}\} = \{x\}
3. Partea întreagă a părții fracționare a oricărui număr real este egală cu 0:
[\{x\}]=04. Partea fracționară a părții întregi a oricărui număr real este egală cu 0:
\{[x]\} =05. Proprietatea de mai jos se deduce din definiția părții întregi ( [x] \leq x < [x] +1 ):
x -1 < [x] \leq x
Pentru \forall x \in \R; \space \forall n \in \Z avem următoarele proprietăți:
6. Partea întreagă a sumei dintre un număr real și un întreg este egală cu suma dintre partea întreagă a numărului real și numărul întreg:
[x +n] = [x] +n
7. Partea fracționară a sumei dintre un număr real și un întreg este egală partea fracționară a numărului real:
\{x + n\} = \{x\}Alte proprietăți pentru partea întreagă și partea fracționară
1. Pentru \forall x, y \in \R avem următoarea inegalitate:
[x] +[y] \leq [x+y]\leq [x] +[y] +1
1.1 Din care deducem \forall n \in \N^* :
n\cdot[x] \leq[n\cdot x] < n\cdot [x]+n
sau:
0\leq[n\cdot x]-n\cdot [x]< n
2. Pentru \forall x \in \R; \space \forall n \in \N^* avem:
\Bigg[\frac{[n\cdot x]}{n}\Bigg] = [x]3. Egalitatea lui Hermite \forall x \in \R; \space \forall n \in \N^* :
[n\cdot x] = [x] + \Bigg[x +\frac{1}{n}\Bigg]+ \Bigg[ x +\frac{2}{n}\Bigg]+...+\Bigg[x +\frac{n-1}{n}\Bigg]3.1 Caz particular al egalității lui Hermite pentru n = 2:
[2x] = [x] +\Big[x +\frac{1}{2}\Big]4. Pentru \forall x, y \in \R avem:
[-x] + [x] =\begin{cases}
\space\space\space 0 & ; & x \in \Z \\
-1 &; & x \in \R \setminus \Z
\end{cases}5. Un număr real este mai mic decât un număr întreg dacă și numai dacă partea sa întreagă este mai mică decât numărul întreg.
x < n \iff[x] < n
Observații:
Partea întreagă nu este rotunjire
Partea întreagă a unui număr este cel mai mare întreg care nu este mai mare decât numărul dat, în timp ce rotunjirea implică trecerea la cel mai apropiat întreg, fie în sus, fie în jos, în funcție de partea fracționară.
Partea întreagă nu este trunchiere
Trunchierea unui număr real elimină pur și simplu partea sa fracționară, fără a rotunji numărul în nicio direcție. Pentru numerele pozitive, rezultatul trunchierii este similar cu cel al părții întregi. Astfel deși rezultatele pot părea similare pentru numerele pozitive, diferența devine evidentă în cazul numerelor negative.
Partea fracționară a numerelor negative este pozitivă
Partea fracționară a oricărui număr real este întotdeauna mai mare sau egală zero și mai mică decât 1, indiferent dacă numărul inițial este pozitiv sau negativ.
Aplicații practice pentru partea întreagă și partea fracționară
Funcțiile de parte întreagă și parte fracționară sunt extrem de utile. În programare sunt folosite într-o varietate largă de contexte pentru a simplifica calculele, a gestiona datele și a îmbunătăți eficiența algoritmilor. În domeniul financiar, funcțiile de parte întreagă și parte fracționară au aplicabilități importante, facilitând calculul precis și gestionarea eficientă a datelor financiare. De-asemenea aceste funcții permit inginerilor să efectueze calcule precise, să modeleze comportamente fizice și să optimizeze soluții tehnologice.
Probleme rezolvate pentru partea întreagă și partea fracționară
Puteți găsi o ecuație rezolvată cu parte întreagă și parte fracționară pentru gimnaziu pe schoolnuggets.
Iar pentru liceu o problema cu parte întreagă și logaritm aici și una cu parte întreagă și integrala aici
Referințe:
Axioma lui Arhimede
Parte întreagă și parte fracționară
Partie entière et partie fractionnaire
Floor and ceiling functions



