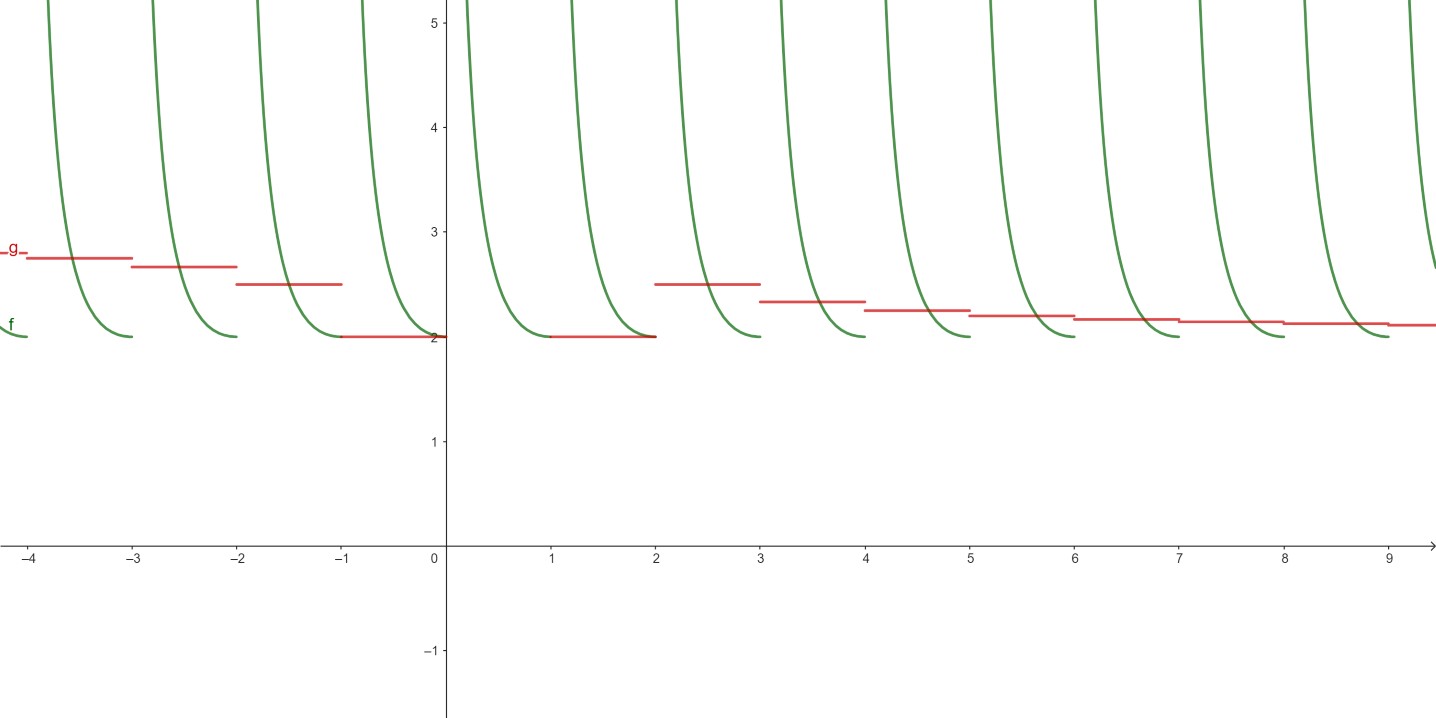
Aceasta ecuație cu parte întreagă și parte fracționară a fost publicată în grupul Comunitatea profesorilor de matematică din România.
Rezolvați ecuația \{x\} + \large\frac{1}{\{x\}} = 2 + \Big\{\large\frac{1}{[x]}\Big\} , unde [a] și {a} reprezintă partea întreagă respectiv partea fracționară a numărului real a.
Din definiția părții întregi știm că:
\forall x \in R, \space x = [x] + \{x\}avem proprietățile:
x\leq [x] < x + 1 \\[1em]
0 \leq \{x\} <1Înainte de a începe rezolvarea problemei analizăm condițiile de existența și trebuie să considerăm cazurile în care numitorul este nenul : {x} ≠ 0 și [x] ≠ 0.
\{x\} \neq 0 \iff x \notin \Z \\[1em]
[x] \neq 0 {\iff} x \notin [0,1)Putem considera discuția pe fiecare interval (k, k+1) \space \forall k \in \Z^* . Deci vom avea:
\forall k \in \Z^*, [x] = k \implies \\[1em]
\{x\} = x - k \\[1em]
\Bigg\{\frac{1}{[x]}\Bigg\} ={\frac{1}{k}}În continuare von nota cu c_k = 2 + \Big\{\large\frac{1}{k}\Big\}
\space \forall k \in (k , k+1) , k \in \Z^* \\[1em]
\{x\} + \frac{1}{\{x\}} = 2 + \Bigg\{\large\frac{1}{[x]}\Bigg\}
\iff\\[1em]
x-k + \frac{1}{x-k} = c_k \iff\\[1em]
(x-k )^2 + 1 = c_k\cdot(x-k) \iff\\[1em]
x^2 -2kx + k^2 + 1 = c_kx - kc_k \iff\\[1em]
x^2-2kx-c_kx+k^2+kc_k+1=0 \iff\\[1em]
x^2 -(2k+c_k)x+k^2+kc_k+1 =0Avem acum o ecuație de gradul 2 căreia îi calculăm soluțiile.
\Delta = (2k+c_k)^2-4(k^2+kc_k+1) \iff \\[1em] \Delta = 4k^2+4kc_k+c_k^2-4k^2-4kc_k-4 \iff \\[1em] \Delta=c_k^2-4
Dar c_k = 2 + \Big\{\large\frac{1}{k}\Big\} \implies c_k^2 - 4>0 \implies \Delta >0 . Deci ecuația va avea soluțiile:
x_{1,2}=\frac{2k+c_k\pm\sqrt{c_k^2-4}}{2} \iff \\[1em]
x_{1,2}=k+\frac{c_k\pm\sqrt{c_k^2-4}}{2} \iff Însă
\frac{c_k +\sqrt{c_k^2-4}}{2} = \frac{2 + \Big\{\large\frac{1}{k}\Big\} +\sqrt{\Big( 2 + \Big\{\large\frac{1}{k}\Big\} \Big)^2-4} }{2} \implies\\[1em]
\frac{c_k +\sqrt{c_k^2-4}}{2} > 1deci pentru x = c_k+\sqrt{c_k^2-4} \implies x > k +1 x nu convine deoarce x \in (k, k+1) \space \forall k \in \Z^* . Deci ne rămîne o singura soluție:
x=k+\frac{c_k-\sqrt{c_k^2-4}}{2}
De unde obținem că aceasta ecuație cu parte întreagă și fracționară are o infinitate de soluții de forma:
[x]+\frac{2 + \Big\{\large\frac{1}{[x]}\Big\}-\sqrt{\Big(2 + \Big\{\large\frac{1}{[x]}\Big\}\Big)^2-4}}{2} \\[1em] x \in (k, k+1) \space \forall k \in \Z^*Pe care o mai putem scrie:
x_k=k+\frac{2 + \Big\{\large\frac{1}{k}\Big\}-\sqrt{\Big(2 + \Big\{\large\frac{1}{k}\Big\}\Big)^2-4}}{2} \\[1em] k = [x] \space \text{și} \space x \in (k, k+1) \space \forall k \in \Z^*