Media aritmetică, geometrică și armonică

Media geometrică

Media geometrică a două numere este definită ca rădăcina pătrată a produsului lor:

m_g=\sqrt{a\cdot b}

În general, media geometrică a n numere x1…xn este definită astfel:

m_g = \sqrt[n]{x_1\cdot x_2 \cdot \ldots \cdot x_n}

Considerând această definiție, se evită folosirea mediei geometrice atunci când avem de-a face cu numere negative, pentru a evita complicațiile rădăcinilor de ordin par ale numerelor negative. Mai putem scrie:

m_g = (x_1\cdot x_2\cdot\ldots\cdot x_n)^\frac{1}{n}

Valoarea medie poate fi “reprezentativă” pentru setul de valori. Practic, dacă am înlocui fiecare dintre valori cu m_g, valoarea produsului ar rămâne aceeași.

(m_g)^n=x_1\cdot x_2 \cdot\ldots\cdot x_n

Pentru n 2 sau 3, putem da și o interpretare geometrica acestei medii. Dacă avem două numere, a și b, ne putem imagina un dreptunghi cu laturile de aceste dimensiuni. Aria acestui dreptunghi este ab. Atunci, media geometrică va reprezenta latura unui pătrat care are aceeași arie ca acest dreptunghi.

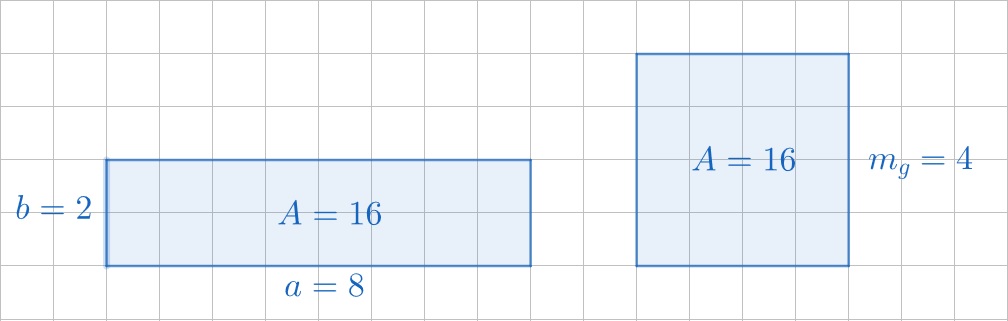
În cazul n = 3, putem considera un paralelipiped dreptunghic, cu muchiile de dimensiuni a, b și c. Volumul său va fi atunci abc. Iar media geometrică va fi latura cubului cu același volum.

Proprietăți ale mediei geometrice

Dacă oricare dintre valorile x₁…x_n este 0, atunci media geometrică este 0.

Acest lucru se poate observa cu ușurință. Dacă oricare dintre numere este 0, atunci produsul lor va fi 0. În concluzie, și media geometrică va fi tot 0.

Inegalitatea mediilor – media geometrică este întotdeauna mai mică decât sau egală cu media aritmetică

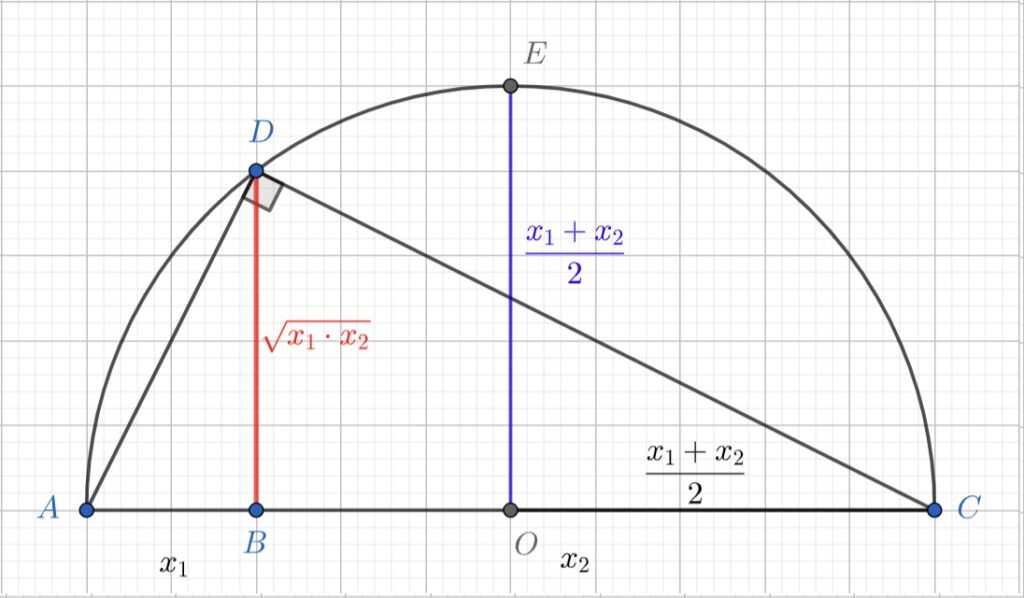
\frac{x_1+x_2+\ldots+x_n}{n}\ge\sqrt[n]{x_1\cdot x_2\cdot\ldots\cdot x_n}

Egalitatea se obține dacă și numai dacă numerele x₁…x_n sunt egale. În cazul particular n=2, această proprietate poate fi vizualizată geometric. Ne aducem aminte de teorema înălțimii, care spune că înălțimea într-un triunghi dreptunghic este egală cu media geometrică a proiecțiilor catetelor pe ipotenuză.

Să ne imaginăm două segmente de lungime x₁ și respectiv x₂ puse cap la cap ca în figura de mai jos:

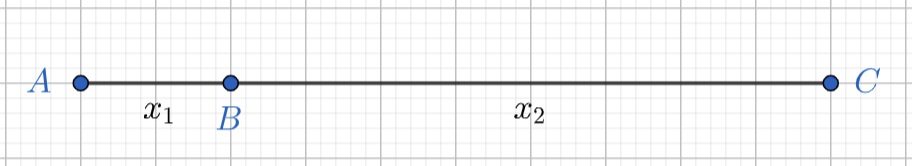
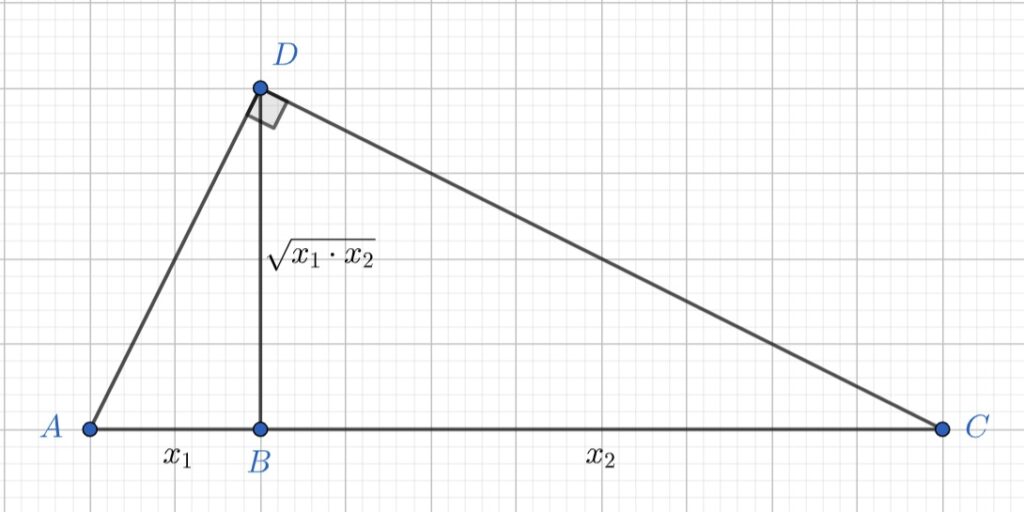
Dacă ridicăm un segment BD perpendicular pe AC în punctul B astfel încât lungimea lui BD să fie egală cu media geometrică a lui x1 și x2, atunci triunghiul ADC va fi dreptunghic în D (reciproca teoremei înălțimii).

Ne aducem aminte de o teoremă a lui Thales (de fapt tot de reciproca ei) care spune că în cercul circumscris triunghiului dreptunghic ipotenuza este diametru. Dacă luăm punctul O ca fiind centrul acestui cerc, atunci OA și OC vor avea valoarea mediei aritmetice a lui x1 și x2.

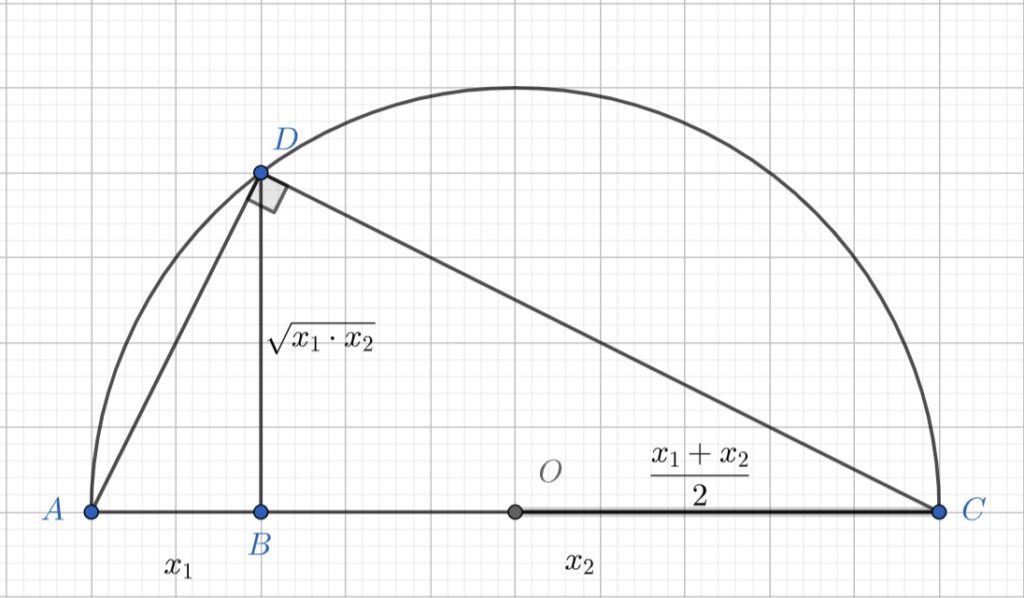
Dar OA și OC sunt raze. Putem duce raza OE perpendiculară pe AC, iar aceasta va fi paralelă cu DB. Se observă că această rază este în general mai mare decât DB, oricare ar fi B pe segmentul AC. Singura excepție este când DB se suprapune peste OE, când B este chiar în O, adică x1 = x2. În acest caz, media aritmetică și media geometrică sunt egale.

Când folosim media geometrică

Media geometrică se folosește atunci când valorile pe care vrem să le mediem au o componentă multiplicativă.

De exemplu, valoarea inițială unui apartament este de 60000€. Pe parcursul a 5 ani, valoarea lui se modifică astfel:

• după primul an, valoarea crește cu 15%
• după al doilea an, valoarea crește cu 20% față de anul precedent
• după al treilea an, valoarea scade cu 15% față de anul precedent
• după al patrulea an, valoarea rămâne la fel
• după al cincilea an, valoarea apartamentului crește cu 5% față de anul precedent

Ne interesează creșterea anuală medie a valorii apartamentului respectiv. După cei cinci ani, valoarea apartamentului se poate exprima astfel:

V=60000\cdot\underbrace{1.15}_{I}\cdot\underbrace{1.20}_{II}\cdot\underbrace{0.85}_{III}\cdot\underbrace{1}_{IV}\cdot\underbrace{1.05}_{V}\\[1em]
V=60000\cdot1.23165\\[1em]
V=73899

Media aritmetică a acestor coeficienți nu ne ajută să calculăm prea exact coeficientul anual mediu de creștere a valorii.

m_a=\frac{1.15 + 1.20 + 0.85 + 1 + 1.05}{5}\\[1em]
m_a=1.05

Aplicând acest coeficient anual, corespunzător unei creșteri de 5%, obținem un V’ egal cu:

V'=60000\cdot1.05^5\\[1em]
V'=60000\cdot1.2762815625\\[1em]
V'=76576.89

V’ diferă semnificativ față de valoarea pe care o are apartamentul după cei cinci ani. Din fericire, media geometrică ne va oferi un coeficient mediu anual care este foarte precis:

m_g=\sqrt[5]{1.15\cdot1.20\cdot0.85\cdot1\cdot1.05}\\[1em]
m_g=\sqrt[5]{1.23165}\\[1em]
m_g=1.042551367...

Aproximăm o creștere medie anuală de 4.26% pe durata celor cinci ani. Datorită modului de calcul al mediei geometrice, valoarea finală obținută prin aplicarea acestui coeficient mediu anual va fi exact valoarea pe care am calculat-o mai sus:

V = 60000\cdot(m_g)^5\\[1em]
V = 60000 \cdot (\sqrt[5]{1.23165})^5\\[1em]
V = 60000\cdot1.23165\\[1em]
V = 73899

Articolul continuă pe pagina următoare