Teorema lui Pitagora reprezintă unul dintre cele mai remarcabile concepte matematice. Are o istorie fascinantă și o gamă vastă de aplicații în diverse domenii.
Teorema afirmă că într-un triunghi dreptunghic, pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor celor două catete.
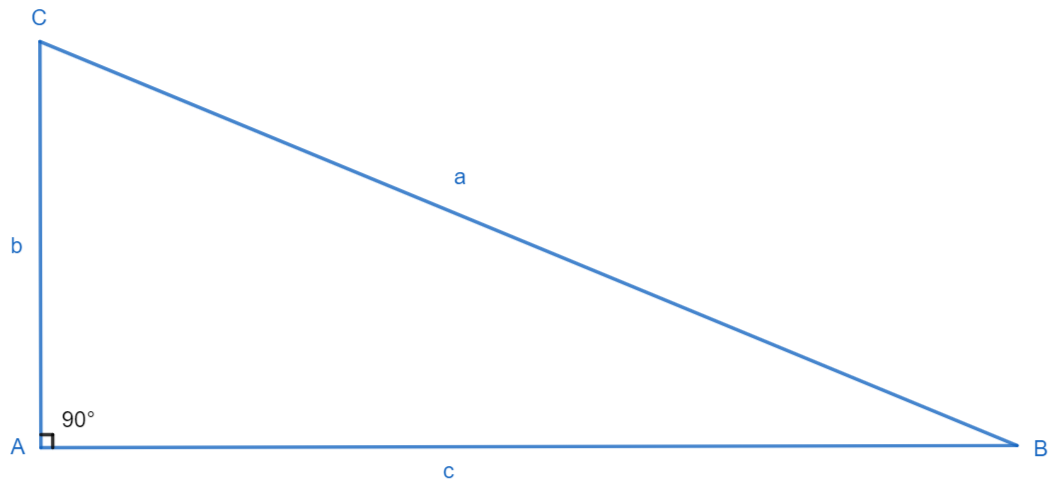
Aceasta poate fi exprimată matematic astfel:
a2 = b2 + c2
unde „a” reprezintă lungimea ipotenuzei, iar „b” și „c” reprezintă lungimile celor două catete.
Teorema lui Pitagora – scurt istoric
Demonstrația originală a teoremei lui Pitagora, conform tradiției, nu este cunoscută în întregime. Nu există un document istoric care să prezinte în mod direct demonstrația făcută de Pitagora sau de școala sa. Deși se crede că Pitagora și discipolii săi au prezentat demonstrații și au dezvoltat explicații pentru diverse concepte matematice, inclusiv pentru teorema care îi poartă numele, acestea nu au fost păstrate în formă scrisă.
Cu toate acestea, există diferite surse și căi prin care s-au transmis informații despre teorema lui Pitagora. Una dintre sursele principale provine din „Elementele” lui Euclid, un text matematic clasic din Grecia antică. În cartea a VI-a, Euclid a prezentat mai multe demonstrații ale teoremei lui Pitagora folosind metoda geometrică. Aceasta este una dintre cele mai cunoscute demonstrații, fiind cunoscută sub numele de „demonstrația lui Euclid„. Demonstrația folosește desene și construcții geometrice pentru a ilustra relația dintre pătratele formate pe laturile unui triunghi dreptunghic.
Alte demonstrații ale teoremei lui Pitagora au fost dezvoltate de matematicieni ulterior, în perioada medievală chiar și în timpurile moderne. Acestea folosesc diverse abordări matematice și metode logice pentru a evidenția relația geometrică fundamentală dintre laturile unui triunghi dreptunghic.
Demonstrație
Una dintre demonstrațiile teoremei lui Pitagora se face calculând aria unui pătrat in două feluri.
Vom considera un pătrat ABCD. Împărțim fiecare latură a sa în două segmente de lungime b, respectiv c, ca în figura de mai jos pentru a obține patru triunghiuri dreptunghice congruente. Observăm că ipotenuzele acestor triunghiuri dreptunghice sunt laturile unui pătrat.
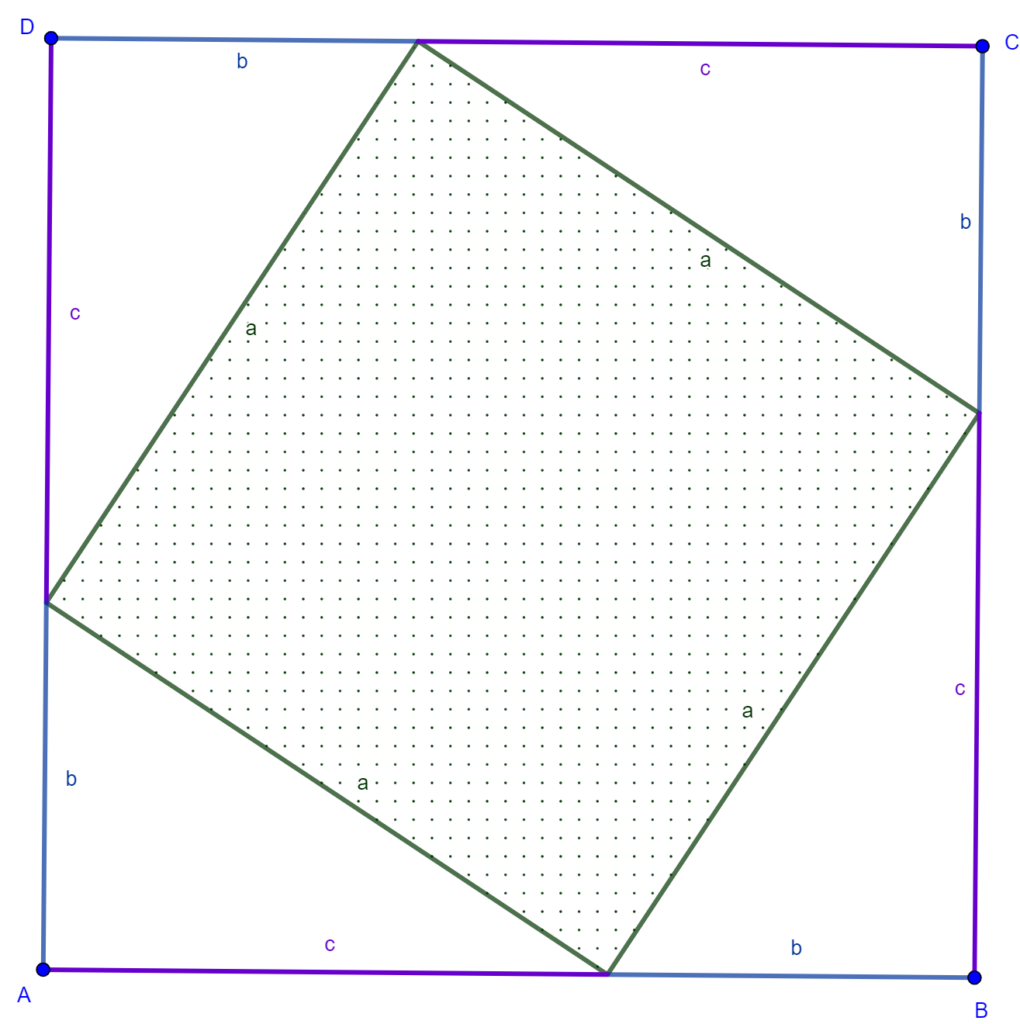
Aria acestui pătrat va fi egala cu (b + c)2 . Aria se poate calcula și ca fiind suma celor patru triunghiuri dreptunghice congruente si a pătratului din mijloc. Deci vom avea:
(b+c)^2 = 4 \cdot \frac{b\cdot c }{2} + a^2 \implies \\[2em]
b^2 +\cancel{2bc} +c^2 = \cancel{2bc} + a^2 \implies \\[2em]
b^2 +c^2 = a^2
Reciproca teoremei lui Pitagora
Dacă într-un triunghi suma pătratelor lungimilor a două dintre laturi este egală cu pătratul lungimii celei de-a treia laturi, atunci acel triunghi este un triunghi dreptunghic. În acest caz, latura pentru care se verifică această egalitate este ipotenuza și unghiul opus acesteia va fi un unghi drept.
Dovezi pre-pitagoreice ale folosirii reciprocii teoremei lui Pitagora
Scrierile antice, inclusiv cele care datează de peste două milenii, evidențiază preocuparea pentru proprietățile matematice ale triunghiurilor dreptunghice. Astfel apar tripletele de numere care satisfac teorema lui Pitagora numite numere pitagoreice. Un astfel de exemplu este tripletul clasic (3, 4, 5).

Într-un articol recent din „Sciences et Avenir,” se vorbește despre o tabletă de lut cunoscută sub numele de Si.427. Pe tabletă este desenat un câmp subdivizat în mai multe forme geometrice: dreptunghiuri, trapeze, triunghiuri dreptunghice care facilitează împărțirea acestuia. Pe Si.427 se găsesc înscrise următoarele triplete pitagoreice (5, 12, 13) și (8, 15, 17). Acesta este considerat cel mai vechi exemplu cunoscut de geometrie aplicată bazată pe analiza numerelor pitagoreice. Numerele pitagoreice sunt folosite pentru a se crea unghiuri drepte precise pentru împărțirea terenului. Acest lucru este necesar când o parte din teren este înstrăinată.
Acest tăbliță subliniază importanța practică a (reciprocei) teoremei lui Pitagora în cadrul civilizațiilor antice în special în domeniul măsurători terenurilor.
Aplicații practice
Cu trecerea timpului, teorema lui Pitagora a evoluat pentru a deveni unul dintre cele mai versatile și utile concepte matematice. Astfel teorema lui Pitagora are o varietate largă de aplicații practice în diferite domenii contemporane:
În navigație, teorema lui Pitagora este esențială pentru calcularea distanțelor și a traseelor. De exemplu, în navigația maritimă sau aeriană, pentru a determina distanța dintre două puncte de pe hartă atunci când cunoaștem coordonatele acestora, se poate folosi teorema lui Pitagora pentru a calcula distanța directă. Acest principiu este crucial pentru planificarea rutelor și a călătoriilor.
În fizică, teorema lui Pitagora este folosită în diverse contexte, inclusiv în mecanica clasică. De exemplu, în cinematică, pentru a calcula distanțele parcurse de obiecte în mișcare. Sau în optică, în relație cu formarea imaginilor în lentile și oglinzi, principiul teoremei lui Pitagora este adesea aplicat pentru a înțelege geometria și relațiile dintre obiecte și sursele de lumină.
În arhitectură și construcții, teorema lui Pitagora este fundamentată în principiile de măsurare și design. În planificarea și construcția clădirilor sau a altor structuri, cunoașterea dimensiunilor și a relațiilor geometrice este esențială pentru a asigura stabilitatea și proporționalitatea acestora. În cazul planificării unui colț drept sau a unui design simetric, teorema lui Pitagora poate fi folosită pentru a asigura precizia măsurătorilor și a unghiurilor.
Mai mult decât atât, teorema lui Pitagora are aplicații extinse în diverse domenii precum cartografie, grafică computerizată, design industrial și chiar în medicină. În imagistica medicală, cum ar fi scanările CT sau RMN, cunoașterea relațiilor geometrice este crucială pentru interpretarea corectă a imaginilor și determinarea dimensiunilor precise ale structurilor anatomice.
Astfel, teorema lui Pitagora rămâne unul dintre conceptele utile și fundamentale în matematică, având implicații vaste în numeroase domenii și jucând un rol esențial în rezolvarea problemelor practice și în avansarea cunoașterii în diverse discipline.



