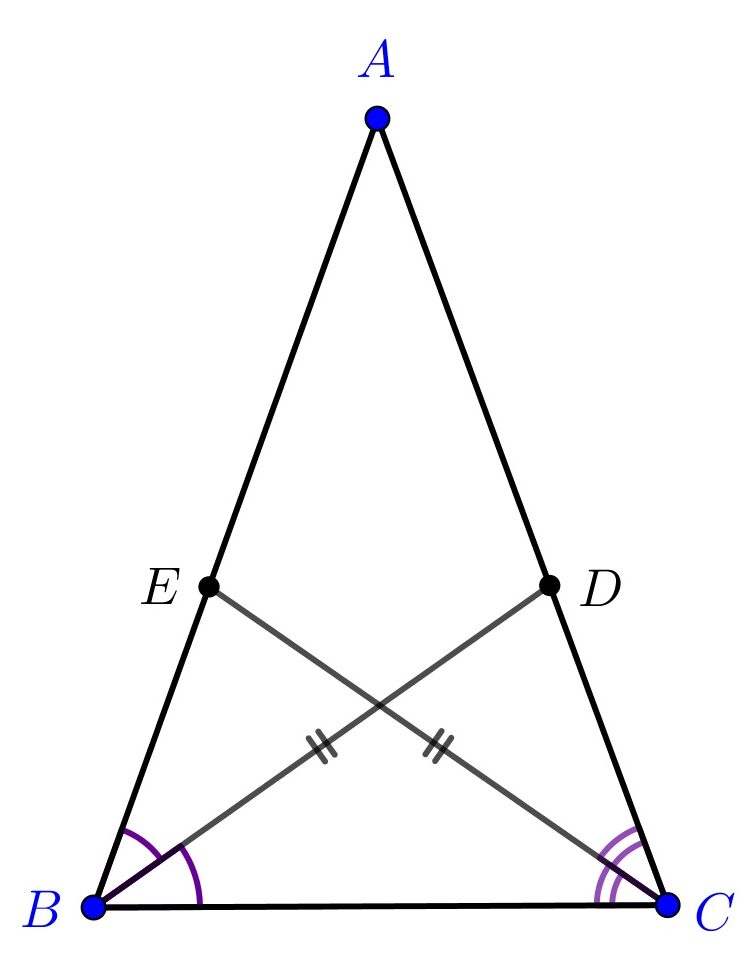
Un triunghi care are două bisectoare interioare egale, măsurate de la vârf la latura opusă, este isoscel.
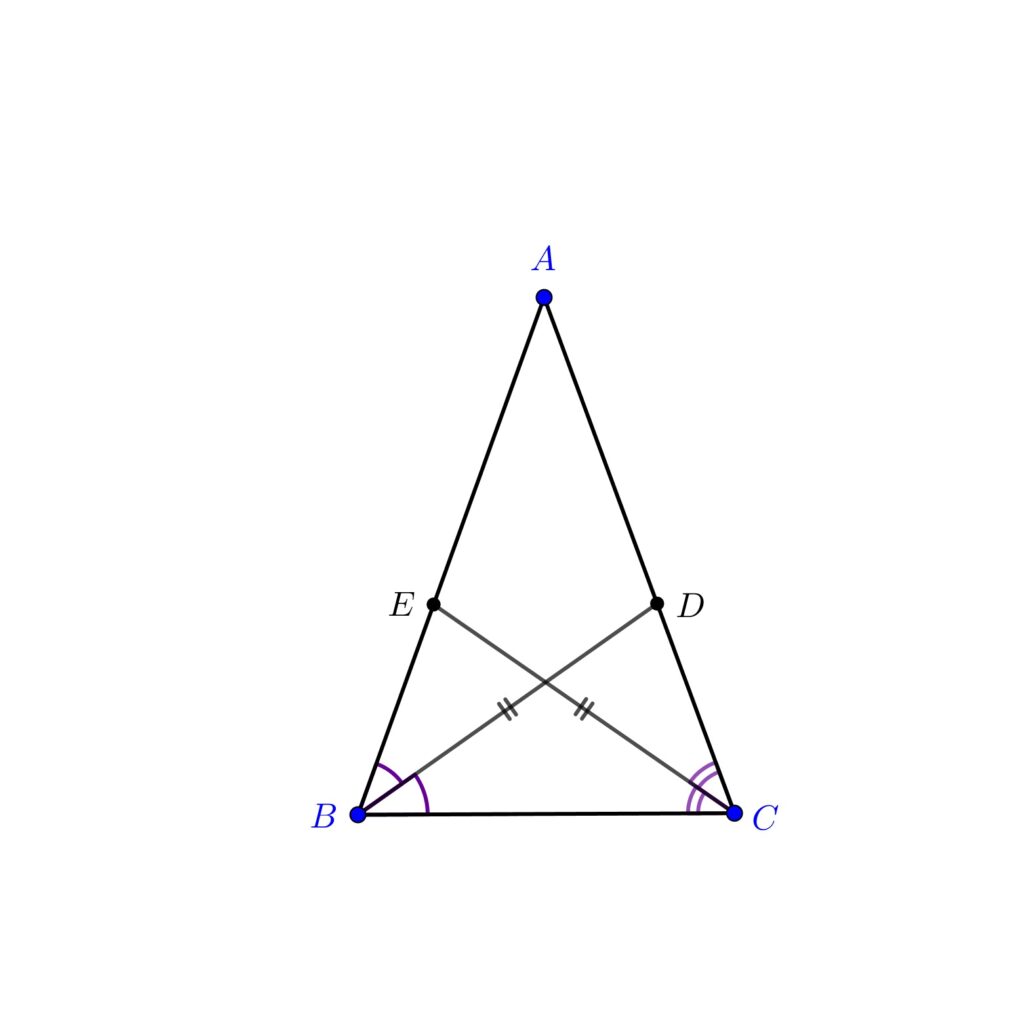
Vom prezenta două metode de demonstrare a acestei teoreme.
Metoda 1
Vom demonstra prin metoda reducerii la absurd aplicată în două cazuri.
Considerăm BD și EC bisectoarele unghiurilor B respectiv C. Presupunem ca AB ≠ AC cu AB < AC. Dar știm că, într-un triunghi, laturii cu lungimea mai mare i se opune unghiul mai mare și reciproc.
AB < AC \implies m(\measuredangle ACB) < m(\measuredangle ABC) \implies \\[1em] \implies \dfrac{m(\measuredangle ACB) }{2} < \dfrac{m(\measuredangle ABC) }{2} De unde obținem că în triunghiurile BCD si BCE vom avea CD > BE.
Vom construi paralelogramul BDFE și vom avea următoarele relații:
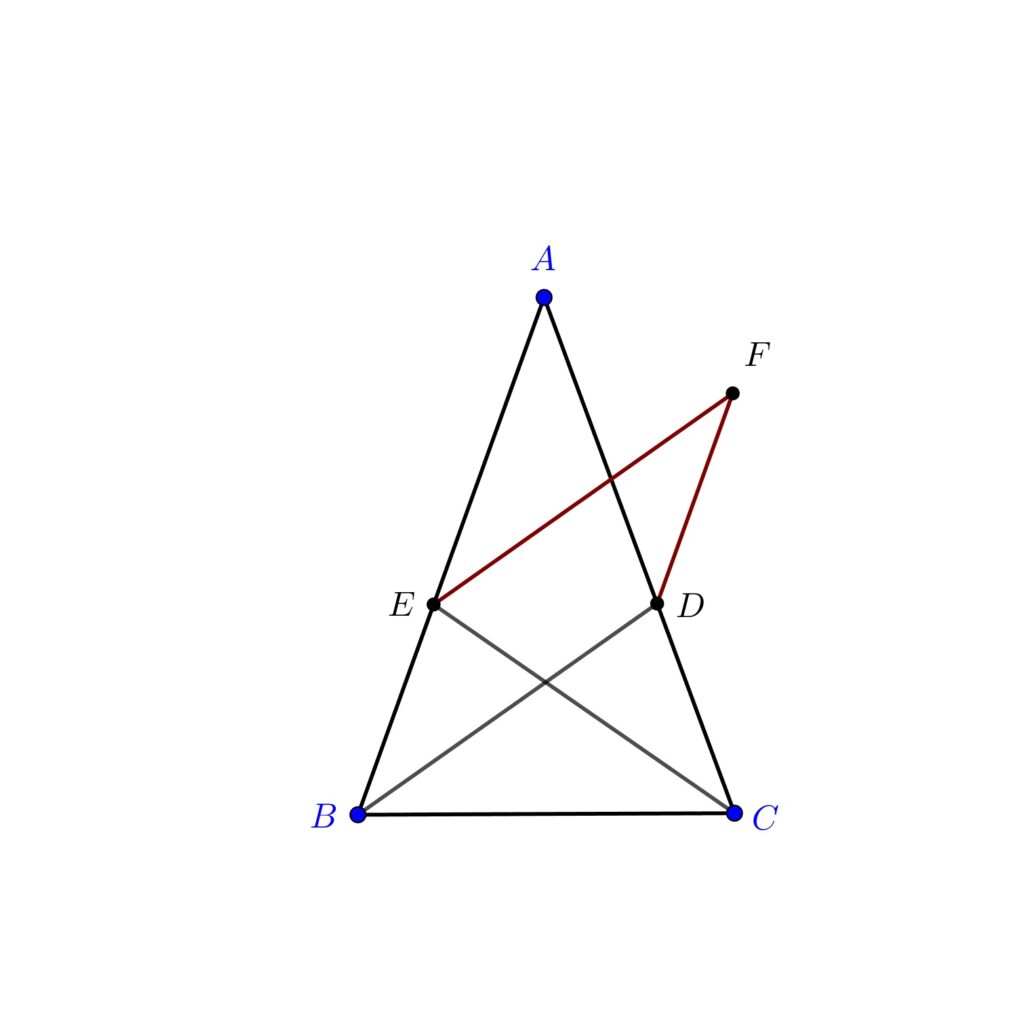
BDFE este paralelogram deci vor fi satisfăcute următoarele relații:
[DF]\equiv[BE]\\[1em]
m(\measuredangle EFD) = m(\measuredangle EBD) = \dfrac{m(\measuredangle ABC) }{2}\\[1em]
[BD]\equiv[EF]\\[1em]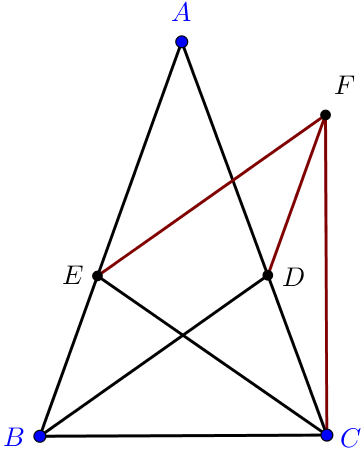
Dar știm din ipoteză că cele două bisectoare sunt congruente, adică [BD] ≡ [CE], deci [EF] ≡ [CE] deci triunghiul ECF este isoscel. Așadar, vom avea:
\left .
\begin{array}{ll}
m(\measuredangle EFD) = \dfrac{m(\measuredangle ABC) }{2} \\[2em]
m(\measuredangle ECD) = \dfrac{m(\measuredangle ACB) }{2} \\[2em]
m(\measuredangle ABC) < m(\measuredangle ACB)\\[1em]
\end{array}
\right
\} \implies \\[1em]
\left .
\begin{array}{ll}
\implies m(\measuredangle EFD) < m(\measuredangle ECD) \\[1em]
\qquad m(\measuredangle EFC) = m(\measuredangle ECF) \\[1em]
\end{array}
\right
\} \implies \\[1em] \implies m(\measuredangle EFC) - m(∡EFD)< m(\measuredangle ECF) - m(∡ECD) \implies \\[1em]
\implies m(∡DFC)< m(\measuredangle DCF)
Vom aplica din nou faptul că într-un triunghi laturii cu lungimea mai mare i se opune unghiul mai mare și reciproc și vom obține DC < DF. Dar [DF] ≡ [BE], de unde obținem că DC < BE, ceea ce este în contradicție cu CD > BE. Deci presupunerea făcută inițial că AB < AC este falsă.
Vom demonstra în mod analog faptul că presupunerea AC < AB este falsă deci nu putem avea decât egalitate.
Metoda 2
Știm că lungimea bisectoarei ia care pleacă din unghiul A este dată de următoarea relatie:
i_a=\frac{2bc\cdot cos\frac{A}{2}}{b+c}Știm de asemenea că bisectoarele care pleacă din unghiurile B respectiv C sunt egale, deci vom avea:
i_b = i_c \implies \\[1em]\implies
\frac{\cancel{2a}c\cdot cos\frac{B}{2}}{a+c} =\frac{\cancel{2a}b\cdot cos\frac{C}{2}}{a+b} \implies \\[1em]\implies\frac{c\cdot cos\frac{B}{2}}{a+c} =\frac{b\cdot cos\frac{C}{2}}{a+b} \implies \\[1em]\implies\frac{ cos\frac{B}{2}}{cos\frac{C}{2}} =\frac{b\cdot( a+c)}{c\cdot (a+b)} Vom aplica din nou metoda reducerii la absurd și vom presupune ca B > C, ceea ce însemnă că b > c.
\left .
\begin{array}{ll}
\dfrac{b\cdot( a+c)}{c\cdot (a+b)} = \dfrac{b\cdot a+ b\cdot c}{c\cdot a+c \cdot b} \\[2em]
b\cdot c = c\cdot b\\[1em]
b > c
\end{array}
\right
\} \implies \\[1em]
\left .
\begin{array}{ll}
\implies \dfrac{b\cdot( a+c)}{c\cdot (a+b)} > 1 \\[2em]
\dfrac{ cos\frac{B}{2}}{cos\frac{C}{2}} =\dfrac{b\cdot( a+c)}{c\cdot (a+b)}
\end{array}
\right
\} \implies \\[1em] \implies \dfrac{ cos\frac{B}{2}}{cos\frac{C}{2}} > 1 \implies
\\[1em] \implies cos\frac{B}{2} > cos\frac{C}{2}
Știm că funcția cosinus este descrescătoare pe intervalul [0, π], deci vom avea:
\left .
\begin{array}{ll}
B, C \in [0,\pi] \implies \dfrac{B}{2} , \dfrac{C}{2} \in [0, \dfrac{\pi}{2}]\\[1em]
cos\dfrac{B}{2} > cos\dfrac{C}{2} \\[1em]
\end{array}
\right
\} \implies \\[1em] \implies \dfrac{B}{2} <\dfrac{C}{2} \implies {B} <{C}B<C contrazice presupunerea făcută.
Vom presupune acum ca B>C și în mod analog vom demonstra că C<B. Deci din cele două presupuneri obținem că B = C deci triunghiul ABC este isoscel.