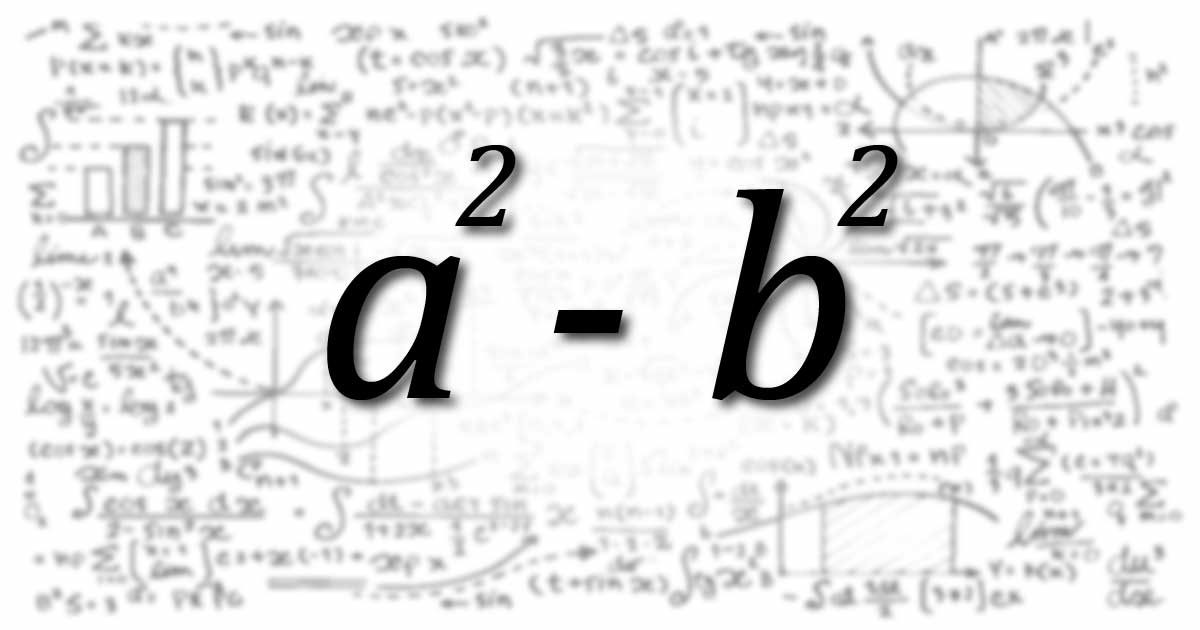Pentru orice a, b, c, f, x reale și n natural, avem următoarele identități algebrice:
(\forall) a,b,c,d,x \in \R \text{ și }n \in \N \text{:}\qquad \qquad\qquad\qquad\qquad\qquad\qquad\qquad
\begin{alignedat}{2}
\textbf{6. } &a^3 + b^3 +c^3 =\\
&= (a+b+ c)^3 -3(a+b)(b+c)(c+a)
\end{alignedat} \\
\begin{alignedat}{2}
\textbf{ 7. }&a^3 + b^3 +c^3 -3abc=
\end{alignedat} \\
\begin{aligned}
=(a+b+ c)(a^2+b^2+c^2-ab -bc -ca) \\[1em]
\end{aligned}\\
\begin{alignedat}{2}
\textbf{ 8. } &a^3 + b^3 +c^3 -3abc=
\end{alignedat} \\
\begin{alignedat}{2}
=\dfrac{1}{2}(a+b+c)[(a-b)^2 +(b-c)^2+(c-a)^2] \\[1em]
\end{alignedat} \\
\begin{alignedat}{2}
\textbf{9. } &a^4 - b^4 = \\
&= (a-b) (a+b) (a^2+b^2)\\[1em]
\textbf{10. } &a^4+ b^4 =\\
& = (a^2+b^2-ab \ \sqrt[]{2}) (a^2+b^2+ab \ \sqrt[]{2})
\end{alignedat}\\[1em]
\begin{alignedat}{1}
\textbf{11. } &a^5 - b^5 =\\
&= (a-b) (a^4+a^3b+a^2b^2+ab^3+b^4)\\[1em]
\textbf{12. } &a^5 + b^5 = \\
& =(a+b) (a^4-a^3b+a^2b^2-ab^3+b^4)
\end{alignedat} \\[1em]
\begin{alignedat}{1}
\textbf{13. } &a^6 + b^6 = (a^3 -2ab^2)^2 + (b^3-2a^2b)^2
\end{alignedat} \\[1em]
\begin{alignedat}{1}
\textbf{14. } & (1+a)(1+a^2+a^4)=\\
&= 1+a+a^2+a^3+a^4+a^5
\end{alignedat} \\[1em]
\\[2em]
\begin{alignedat}{1}
\textbf{15. } &a^n - b^n =
\end{alignedat} \\
\begin{aligned}
=(a-b)(a^{n-1}+a^{n-2}b+..+ab^{n-2}+b^{n-1})
\end{aligned}\\[1em]
\begin{alignedat}{1}
\textbf{16. } &a^{2n} - b^{2n} =
\end{alignedat} \\
\begin{aligned}
=(a^2-b^2)(a^{2n-2}+a^{2n-4}b^2+..+a^2b^{2n-4}+b^{2n-2})
\end{aligned}\\[1em]
\begin{alignedat}{1}
\textbf{17. } &a^{2n+1}+b^{2n+1} =
\end{alignedat} \\
\begin{aligned}=(a+b)(a^{2n}-a^{2n-1}b+...-ab^{2n-1}+b^{2n})
\end{aligned}\\[1em]
\begin{alignedat}{1}
\textbf{18.} &(1+a+a^2+...+a^n)(1+a^{n+1})= \\
&=1+a+a^2+...+a^{2n+1}
\end{alignedat} \\[1em]
\begin{alignedat}{1}
\textbf{19.} &(1+a)(1+a^2)(1+a^4)\cdot...\cdot(1+a^{2^n})= \\
&=1+a+a^2+...+a^{2^{n+1}-1}
\end{alignedat} \\[1em]
\begin{alignedat}{1}
\textbf{20.} & (x+a)(x^2+a^2)\cdot...\cdot(x^{2^{n-1}}+a^{2^{n-1}})=\\
&= \left\{
\begin{array}{ll}
\dfrac{x^{2^{n}}-a^{2^{n}}}{x-a}, \ x \neq a\\\;\\
2^{{n}}\cdot a^{2^{n} -1} , \ x =a \end{array}
\right .
\end{alignedat} \\[2em]
\begin{alignedat}{1}
\textbf{21.} &(1+2^{2n+1}+2^{n+1}) (1+2^{2n+1}-2^{n+1}) = \\
&=1+2^{4n+2}
\end{alignedat} \\[1em]
\begin{alignedat}{1}
\textbf{22.} &\bigg(\displaystyle\sum_{i=1}^{n}a_i^2\bigg) \bigg(\displaystyle\sum_{i=1}^{n}b_i^2\bigg)- \bigg(\displaystyle\sum_{i=1}^{n}a_ib_i\bigg)^2= \\
& = \displaystyle\sum_{i=1}^{n-1}\displaystyle\sum_{j=i+1}^{n}(a_ib_j-a_jb_i)^2
\end{alignedat} \\[1em]
\begin{alignedat}{1}
\textbf{23.} & 1- \dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2n-1}- \dfrac{1}{2n}=\\[1em]
& =\dfrac{1}{n+1} + \dfrac{1}{n+2}+...+ \dfrac{1}{n+n}
\end{alignedat} \\[1em]
\begin{alignedat}{1}
\textbf{24.} &(x+y)^n = \displaystyle\sum_{i=1}^{n}C_n^k\cdot x^{n-k}\cdot y^k \\[2em]
\textbf{25. } & (x-y)^n = \displaystyle\sum_{i=1}^{n}(-1)^k\cdot C_n^k\cdot x^{n-k}\cdot y^k
\end{alignedat} \\[1em]
Mai departe, te-ar putea interesa și o listă de inegalități importante.