Problemă rezolvată dintre subiectele propuse pentru clasa a X-a la ONGM 2020-2021.
Enunț
Într-un triunghi ABC, se știe că AB=4, BC=5, CA=6. Stabiliți care din următoarele afirmații este adevărată:
A.B=3C B.A=2C C.A=3C D.C=2B E.B=2C
Rezolvare
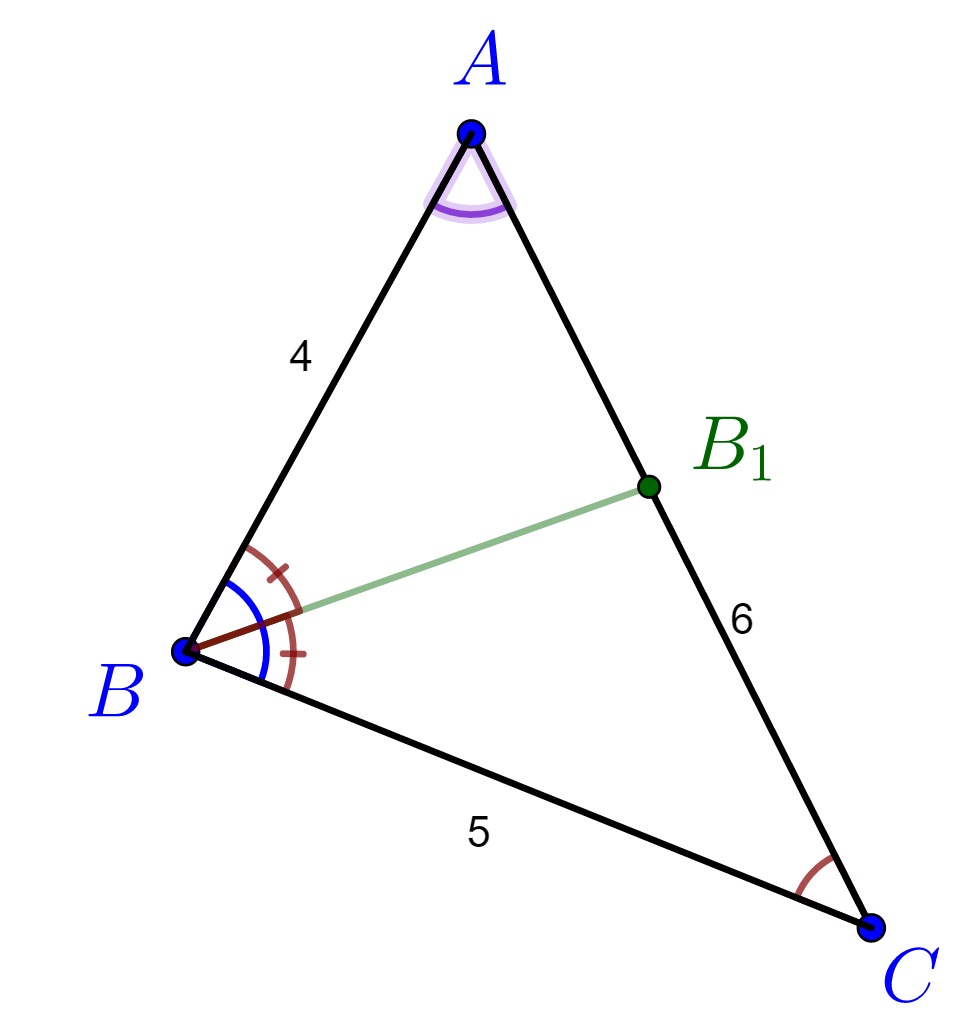
După ce am construit figura geometrică respectând cerințele problemei, am măsurat cu raportorul unghiurile triunghiurilor și am văzut că măsura unghiului C este cca 42°, măsura unghiului B 83° de grade, iar măsura unghiului A 55°. Ținând cont de posibilele erori de măsurare, putem presupune că B ar putea fi de două ori C, iar răspunsul ar fi E. Putem oare să demonstrăm acest lucru ?
Vom construi BB1 bisectoarea unghiului B, și notăm cu ib lungimea bisectoarei din B, BB1. Știm că lungimea bisectoarei este:
i_b= \dfrac{2}{(a+c)}\cdot \sqrt[]{pac\cdot(p-b)} \\\;\\ p = \dfrac{a +b+c}{2}În cazul nostru:
p = \dfrac{ 4 + 5 + 6}{2} \implies p = \dfrac{15}{2} \implies \\ \;\\ \implies i_b= \dfrac{2}{9}\cdot \sqrt[]{\dfrac{15}{2}\cdot 5 \cdot 4 \cdot(\dfrac{15}{2}-6) } \implies \\ \;\\ \implies i_b= \dfrac{2}{9}\cdot \sqrt[]{{15}\cdot 5 \cdot \cancel{2} \cdot\dfrac{3}{\cancel{2}}} \implies \\ \;\\ \implies i_b= \dfrac{2\cdot 15}{9} \implies \\ \;\\ \implies i_b= \dfrac{2\cdot 5}{3} \implies i_b= \dfrac{10}{3}Folosim teorema bisectoarei interioare pentru a găsi lungimea lui B1C.
Din teorema bisectoarei știm că:
\dfrac{AB}{BC} = \dfrac{AB_1}{CB_1} \implies \dfrac{4}{5} = \dfrac{AB_1}{CB_1}\implies \\ \;\\ \implies \dfrac{4+5}{5} = \dfrac{AB_1 + CB_1 }{CB_1} \implies \\ \;\\ \implies \dfrac{4+5}{5} = \dfrac{AC}{CB_1} \implies \\ \;\\ \implies \dfrac{4+5}{5} = \dfrac{6}{CB_1} \implies \\ \;\\ \implies \dfrac{9}{5} = \dfrac{6}{CB_1} \implies \\ \;\\ \implies CB_1 = \dfrac{5 \cdot 6}{9} \implies \\ \;\\ \implies CB_1 = \dfrac{10}{3}Deci BB1 = B1C de unde obținem că triunghiul BB1C este isoscel.
\left .
\begin{array}{ll}
m(\angle B_1BC) = m(\angle B_1CB) \\\;\\
m(\angle B) = 2 \cdot m(\angle B_1BC)
\end{array}
\right \} \implies \\\;\\ \implies m(\angle B) = 2 \cdot m(\angle B_1CB)Deci B este de două ori C, iar răspunsul este E.



