Problemă rezolvată dintre subiectele propuse pentru clasa a X-a la ONGM 2020-2021.
Enunț
Dacă H este o ortocentrul triunghiului ABC, atunci lungimea segmentului AH este egală cu:
A.RsinA B.2RsinA C.RcosA D.2RcosA E.2rsinA
Rezolvare
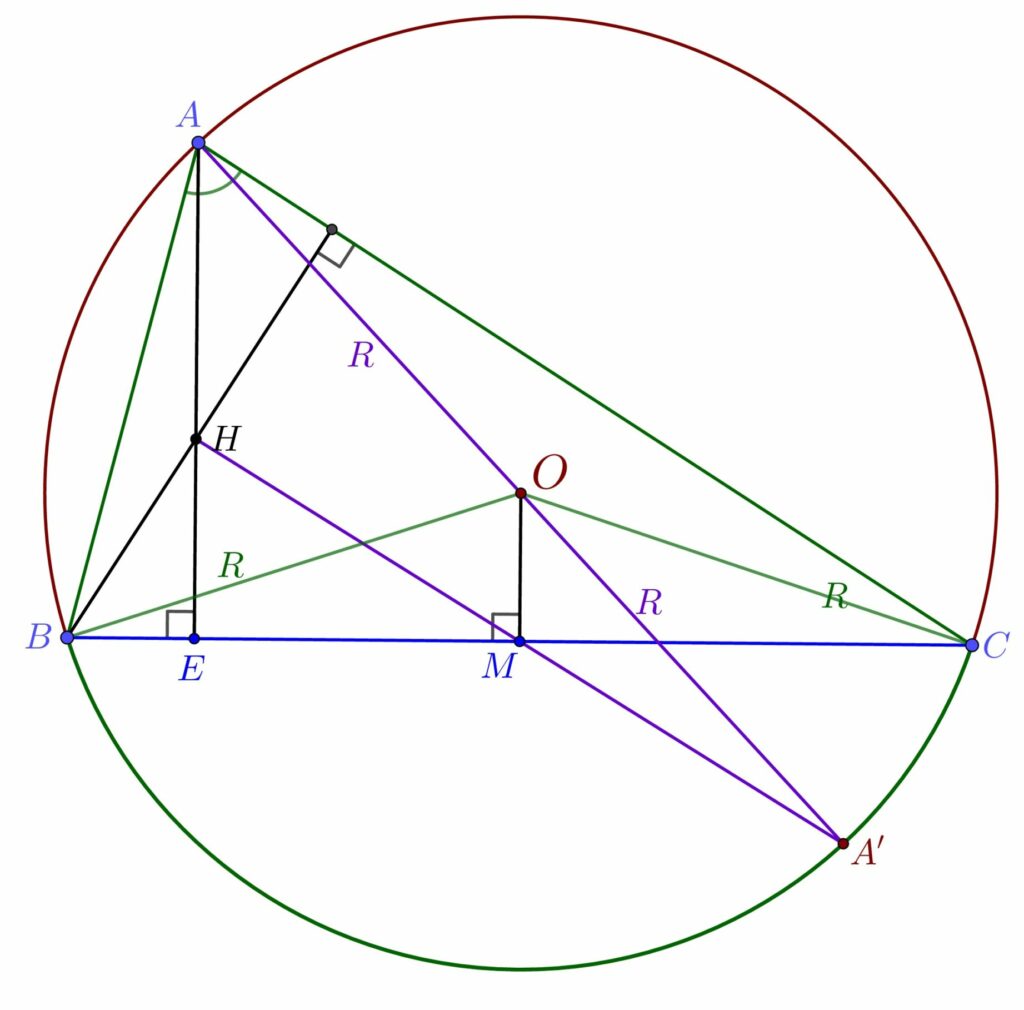
Fie O centrul cercului circumscris triunghiului ABC, AE înălțimea din A, OM mediatoarea lui BC. Prelungim HM până când intersectăm cercul C(O) în punctul A’.
\left .
\begin{array}{ll}
\left .
\begin{array}{ll}
OM \perp BC\\
AE \perp BC
\end{array}
\right \} \implies EA \parallel OM \\
\qquad \qquad \qquad\qquad \ \ \ \ AO = OA'
\end{array}
\right \} \overset{\text{Linie Mijlocie}}{\implies}\\\;\\ \overset{\text{Linie Mijlocie}} {\implies} OM = \dfrac{AH}{2} {\implies} \\\;\\ {\implies} AH = 2 \cdot OM Calculăm aria triunghiului BOC în două moduri diferite:
S_{\triangle BOC} = \dfrac {BO \cdot CO \cdot sin (BOC)}{2} \implies \\\;\\ \implies S_{\triangle BOC} = \dfrac{R\cdot R \cdot sin (BOC)}{2} \\\;\\
\left .
\begin{array}{ll} S_{\triangle BOC} = \dfrac{R^2 \cdot sin (BOC)}{2} \\\;\\
S_{\triangle BOC} = \dfrac {OM \cdot BC}{2}
\end{array}
\right \}
\implies \\\;\\ \implies \dfrac {OM \cdot BC}{\cancel{2}} = \dfrac{R^2 \cdot sin (BOC)}{\cancel{2}} \implies \\\;\\ \implies OM = \dfrac {R^2 \cdot sin (BOC)}{BC}
Unghiul BOC este unghi la centru, deci va avea măsura egală cu a arcului subîntins. Unghiul BAC subîntinde același arc de cerc, BC, însă este unghi pe cerc, deci va avea măsura egală cu jumătatea măsurii arcului BC.
\left .
\begin{array}{ll}
m (\angle BOC) = m(\overset{\frown}{BC})\\\;\\
m (\angle BAC) = \dfrac{m(\overset{\frown}{BC})}{2}
\end{array}
\right \} \implies \\ \;\\ \implies m (\angle BOC) = 2 \cdot m (\angle BAC) \implies \\\;\\ \implies sin (BOC) = sin (2A) \implies \\\;\\ \implies sin (BOC) = 2sin(A)cos(A) \left .
\begin{array}{ll}
OM = \dfrac {R^2 \cdot sin (BOC)}{BC}\\\;\\
sin (BOC) =2 sin(A) cos(A) \\\;\\
\end{array}
\right \}
\implies \\ \;\\
\left .
\begin{array}{ll}
\implies OM = \dfrac {R^2 \cdot 2 sin(A) cos(A)}{BC} \\\;\\
\dfrac{BC}{sin(A)} = 2R \Leftrightarrow \dfrac{R}{BC} = \dfrac{1}{2sin(A)} \end{array}
\right \} \implies \\ \;\\ \implies OM = \dfrac {R \cdot \cancel{2 \cdot sin(A)} \cdot cos(A)}{\cancel{2 \cdot sin(A)}} \implies \\ \;\\ \left .
\\ \;\\
\begin{array}{ll}
\implies OM = R \cdot cos(A) \\
\qquad \ AH = 2 \cdot OM
\end{array}
\right \} \implies \\ \;\\ \implies AH = 2R \cdot cos(A)Răspunsul este D, 2RcosA.