Cazuri particulare de poligoane regulate
În funcție de numărul laturilor acestea pot fi cu:
– 3 laturi: triunghi echilateral cu centrul cercului circumscris intersecția mediatoarelor
L_3=R\cdot\sqrt 3\\\;\\
a_3=\frac{R}{2}\\\;\\
S_3=3R^2\cdot\frac{\sqrt[]{3}}{4}
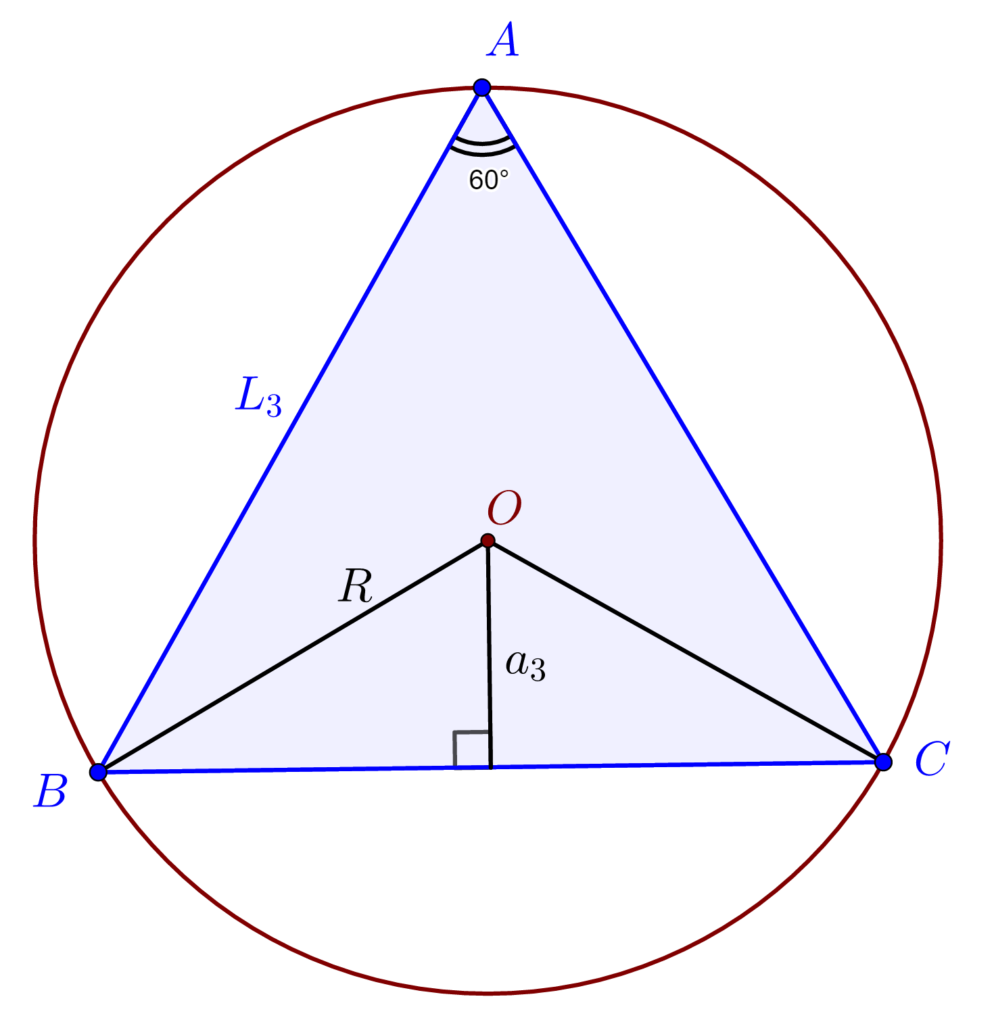
– 4 laturi: pătratul, cu centrul cercului circumscris intersecția diagonalelor
L_4=R\cdot\sqrt 2\\\;\\
a_4=R\cdot\frac{\sqrt 2}{2}\\\;\\
S_4=2\cdot R^2
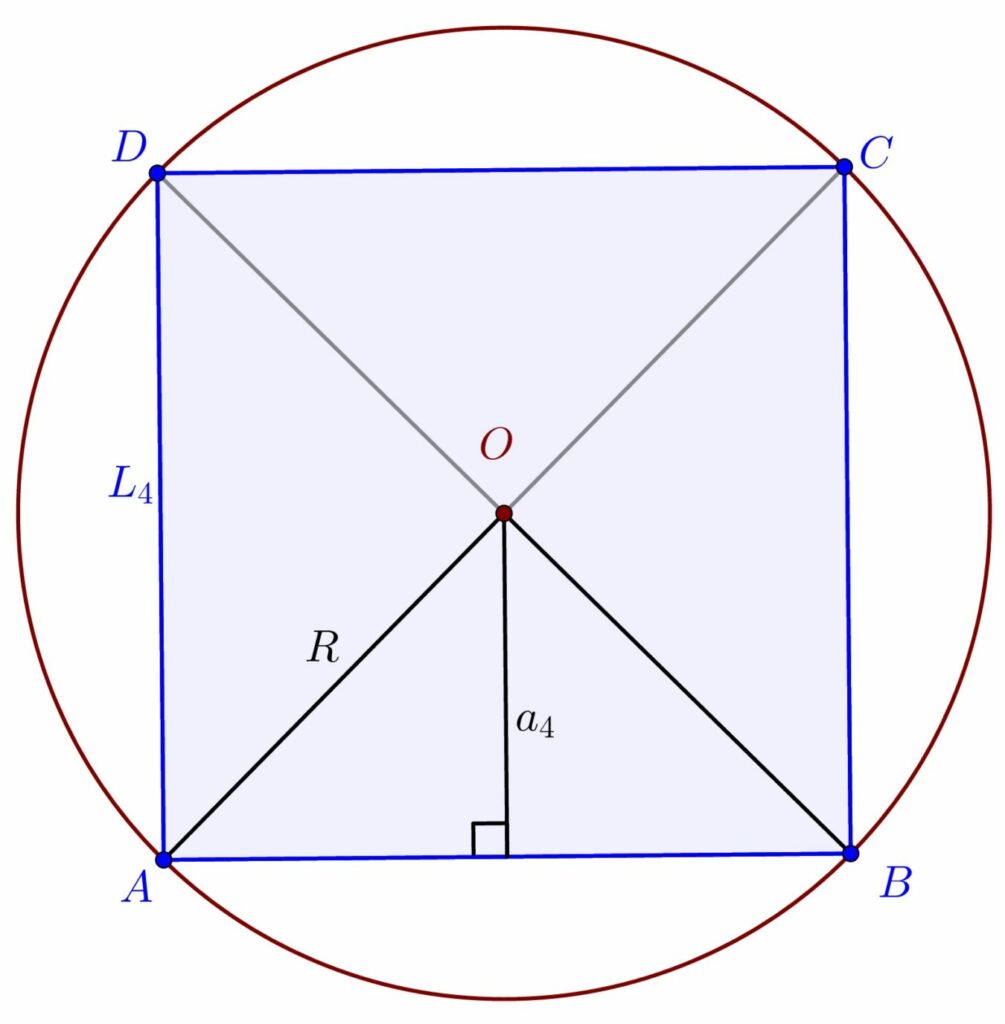
– 5 laturi: pentagonul convex
L_5=R\cdot\sqrt[]{\frac{5-\sqrt[]{5}}{2}} \\\;\\
a_5=R\cdot {\frac{\sqrt[]{5}+1}{4}} \\\;\\
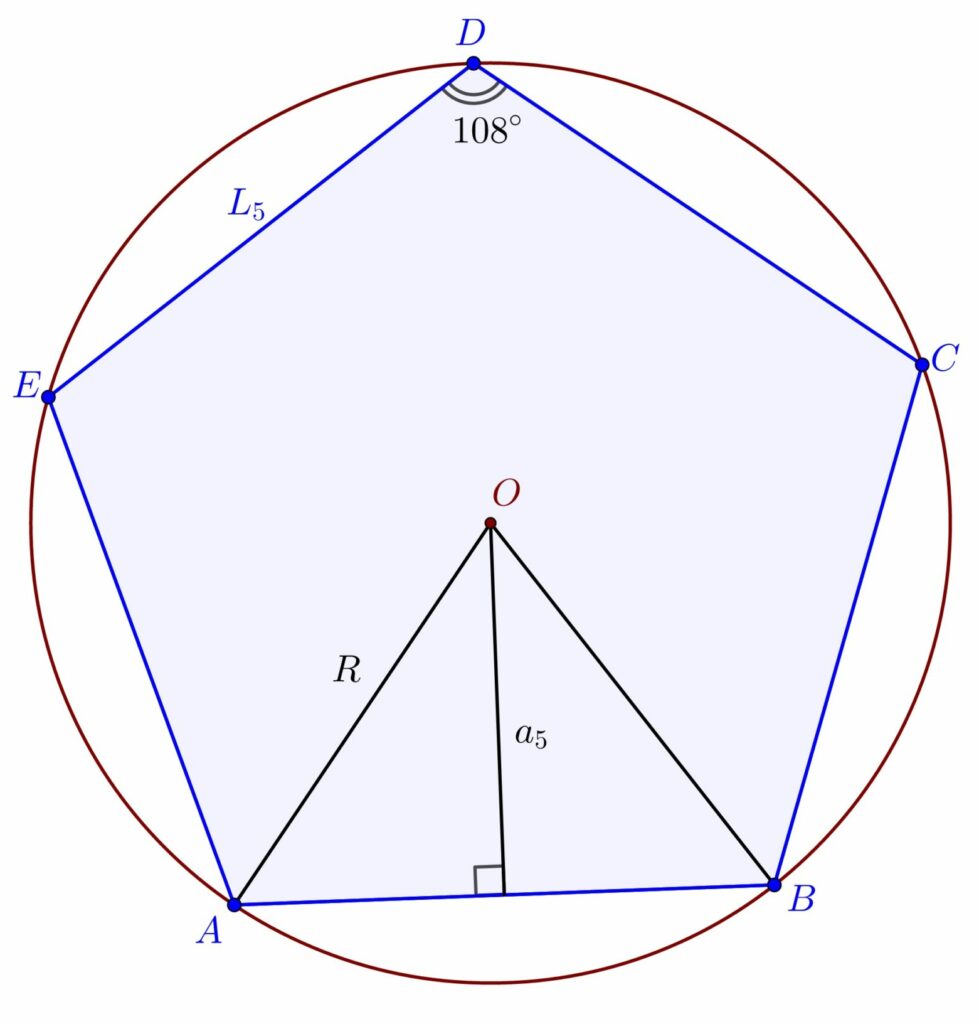
S_5=\frac{5R^2}{4}\cdot\sqrt[]{\frac{5+\sqrt[]{5}}{2}} \\\;\\– 6 laturi: hexagonul convex
L_6=R\\\;\\
a_6=R\cdot\frac{\sqrt 3}{2}\\\;\\
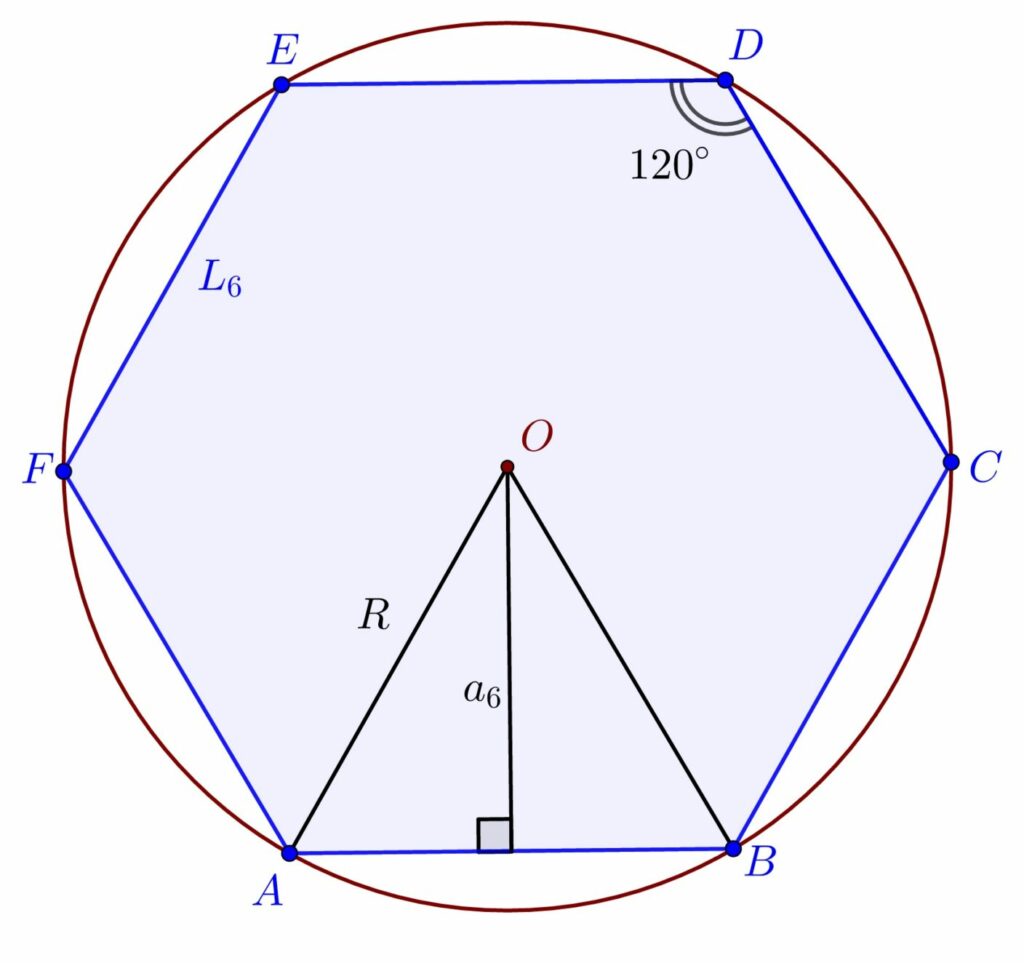
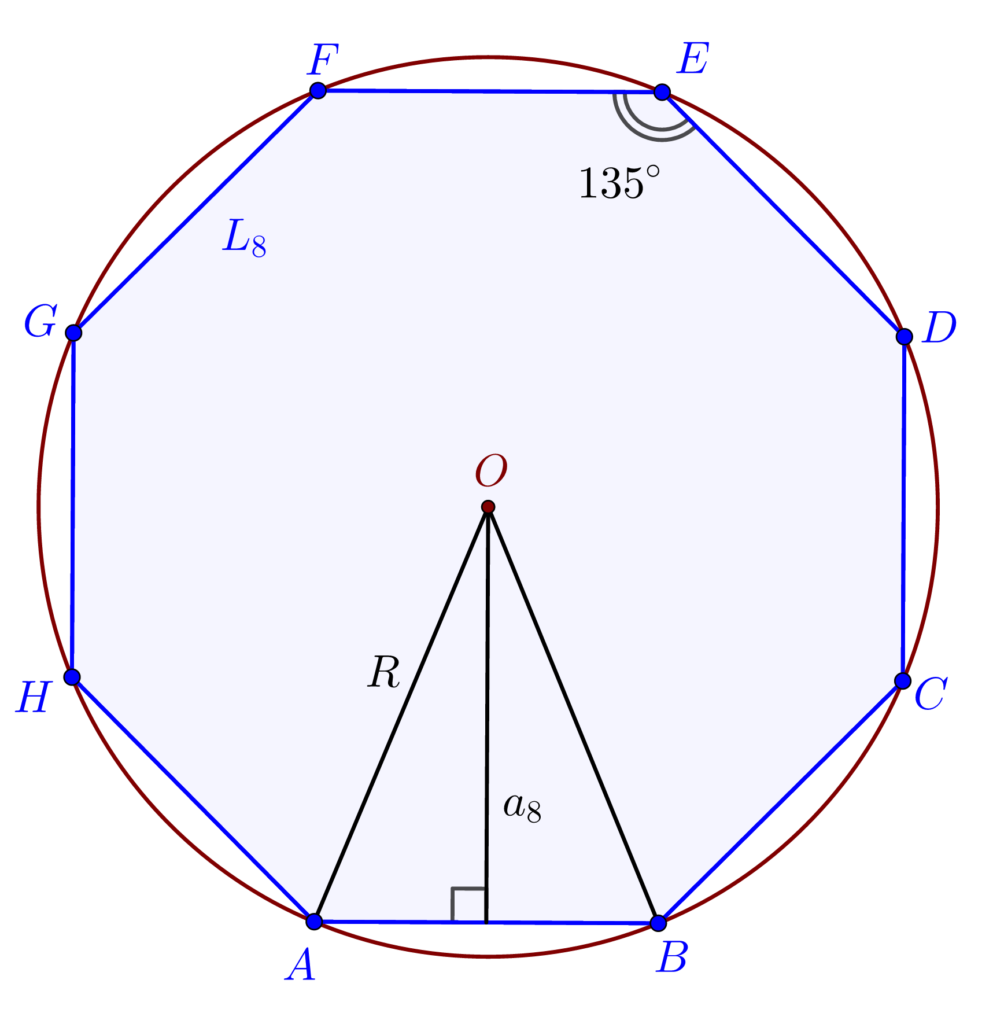
S_6=\frac{3\sqrt 3}{2}\cdot R^2– 8 laturi: octogonul convex
L_8=R\cdot\sqrt []{2-\sqrt[]{2}}\\\;\\
a_8= \frac{R}{2}\cdot\sqrt []{2 + \sqrt []{2 }}\\\;\\
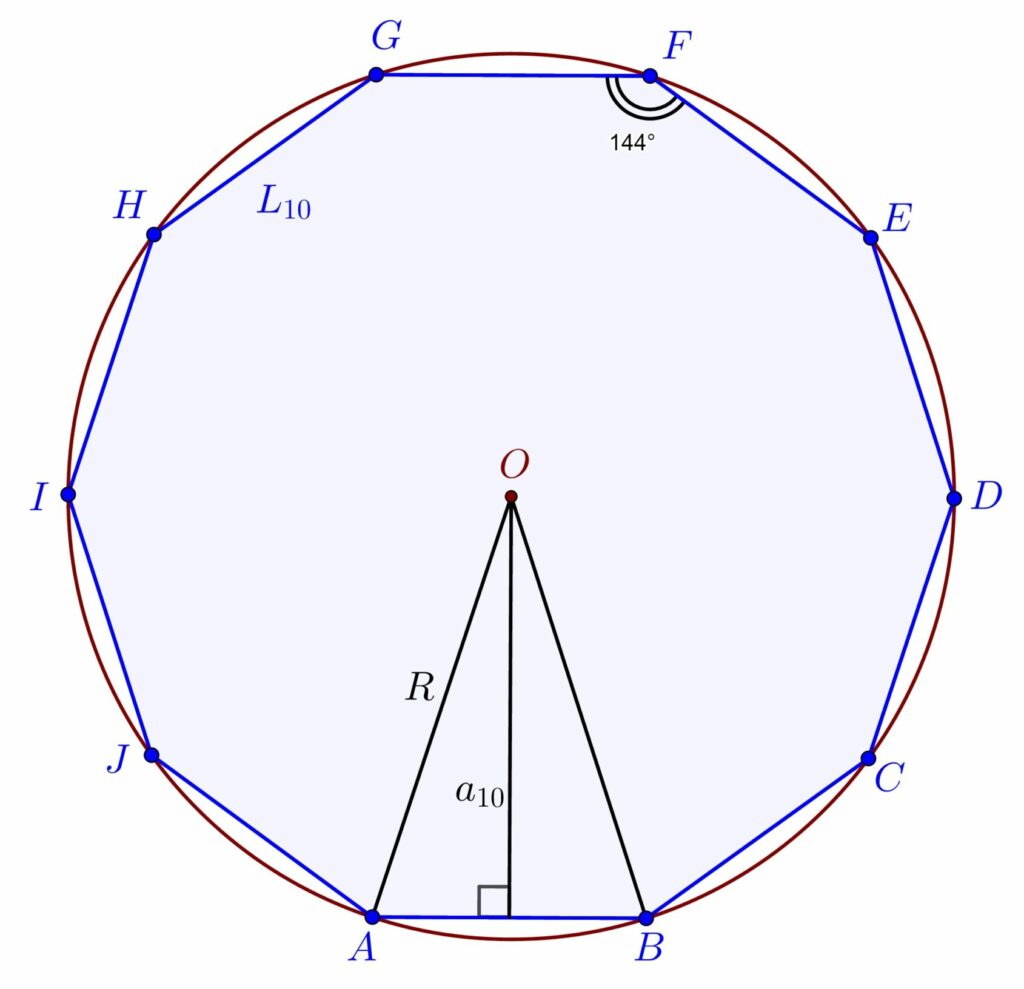
S_8=2\cdot\sqrt[]{2}R^2– 10 laturi: decagonul convex
L_{10}=\frac{R}{2}\cdot(\sqrt []{5}-1)\\\;\\
a_{10}=R\cdot\sqrt []{\frac{5 + \sqrt [] {5} }{2}}\\\;\\
S_{10}=\frac{5R^2}{2}\cdot\sqrt []{\frac{5-\sqrt []{5 }}{ 2} }
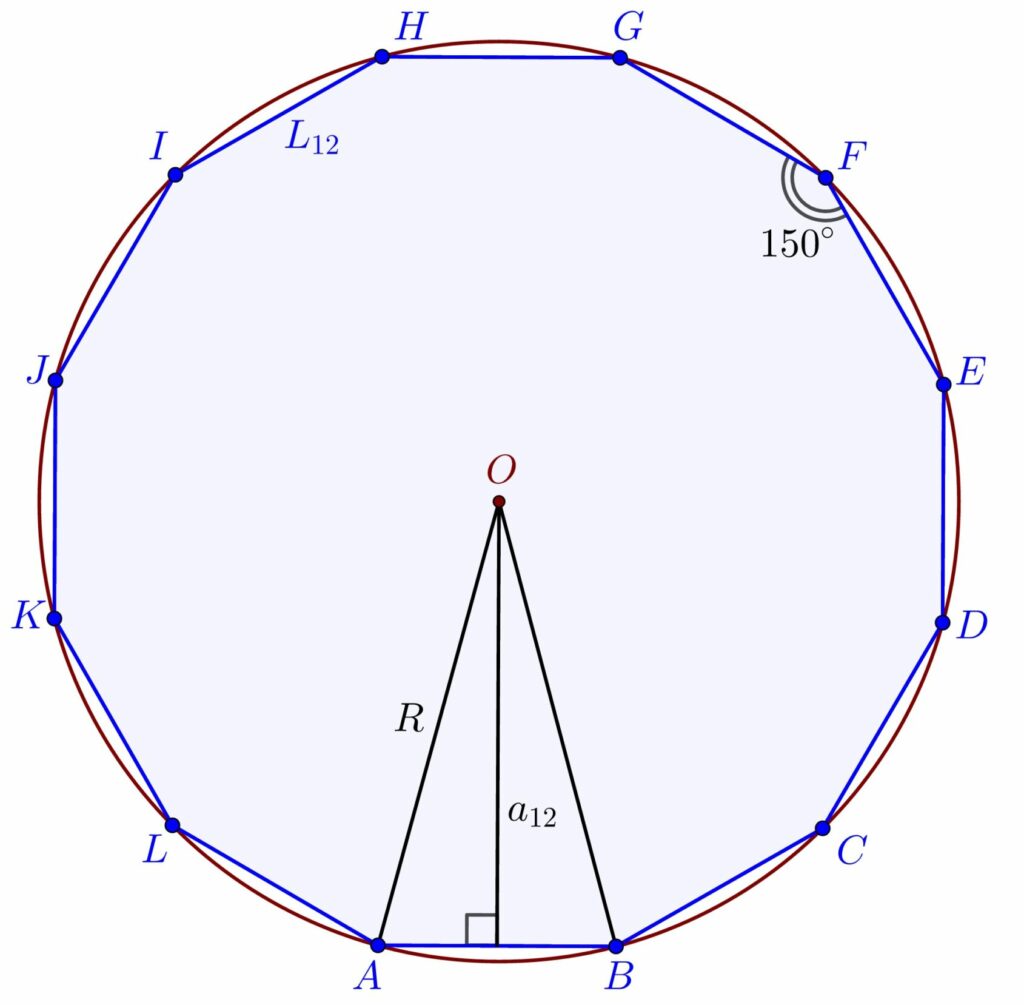
– 12 laturi: dodecagonul convex:
L_{12}=\frac{R}{2}\cdot(\sqrt []{6}-\sqrt []{2})\\\;\\
a_{12}= \frac{R}{4}\cdot(\sqrt []{6}+\sqrt []{2})\\\;\\
S_{12}=3\cdot R^2Dacă știm valorile pentru lungimea laturii și apotemei unui poligon regulat cu n laturi, atunci putem calcula lungimile laturilor și apotemelor poligoanelor regulate cu de doua ori mai multe laturi aplicând formulele de mai jos:
L_{2n}=\sqrt []{2R^2-R\cdot\sqrt[]{4R^2-L_n^2}}\\\;\\
a_{2n}= \frac{1}{2}\cdot\sqrt []{2R^2 + R\cdot\sqrt []{4R^2-L_n^2 }}\\\;\\
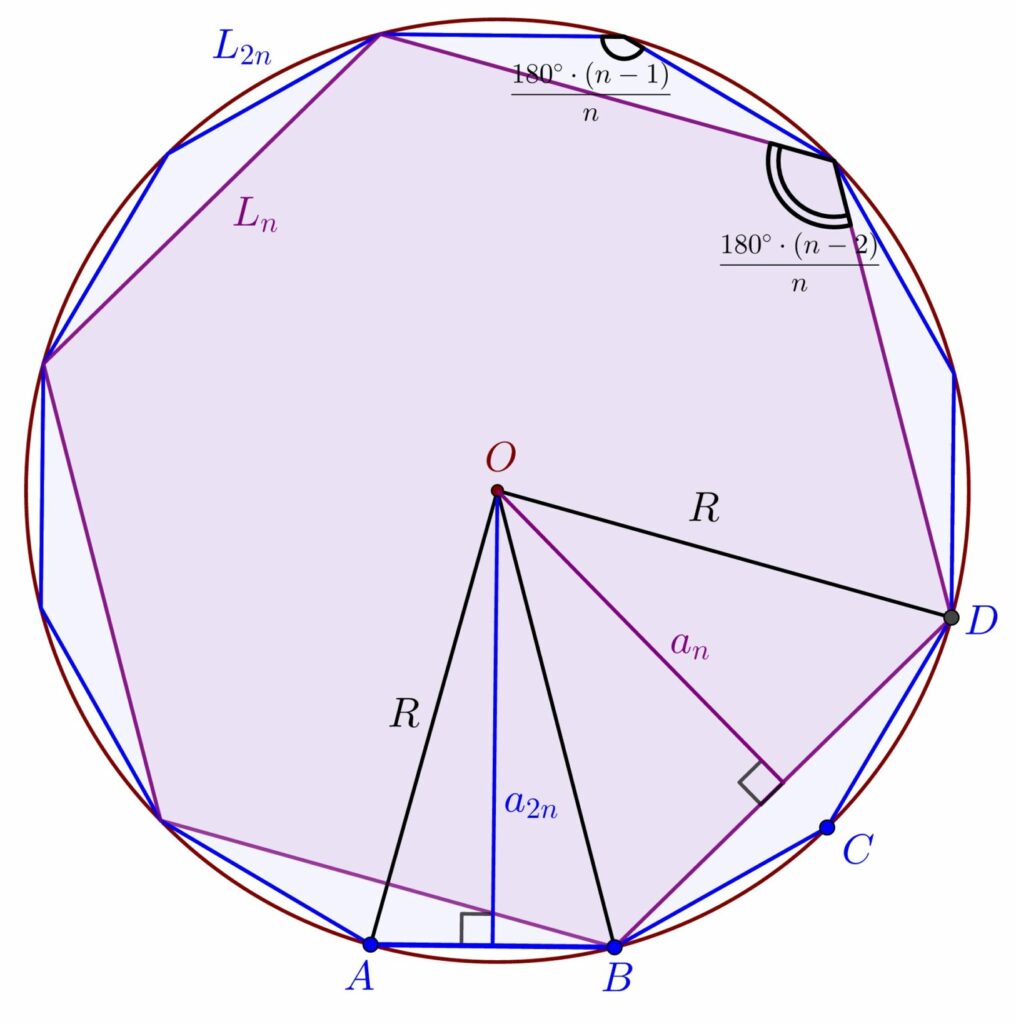
S_{2n}= \frac{P_{2n}\cdot a_{2n}}{2}unde Pn este perimetrul poligonului regulat cu n laturi:
P_n=n\cdot L_n
[the_ad_group id=”102″]
