Poligoanele înscrise în cerc – arii, laturi, apoteme

Poligoanele regulate înscrise în cerc

Un poligon convex cu toate laturile congruente și toate unghiurile congruente se numește poligon regulat. Putem obține un poligon regulat dacă împărțim un cerc în cel puțin 3 arce congruente. Unind punctele de diviziune, se obțin coarde egale deoarece la arce congruente se opun coarde congruente. Astfel obținem un poligon regulat.

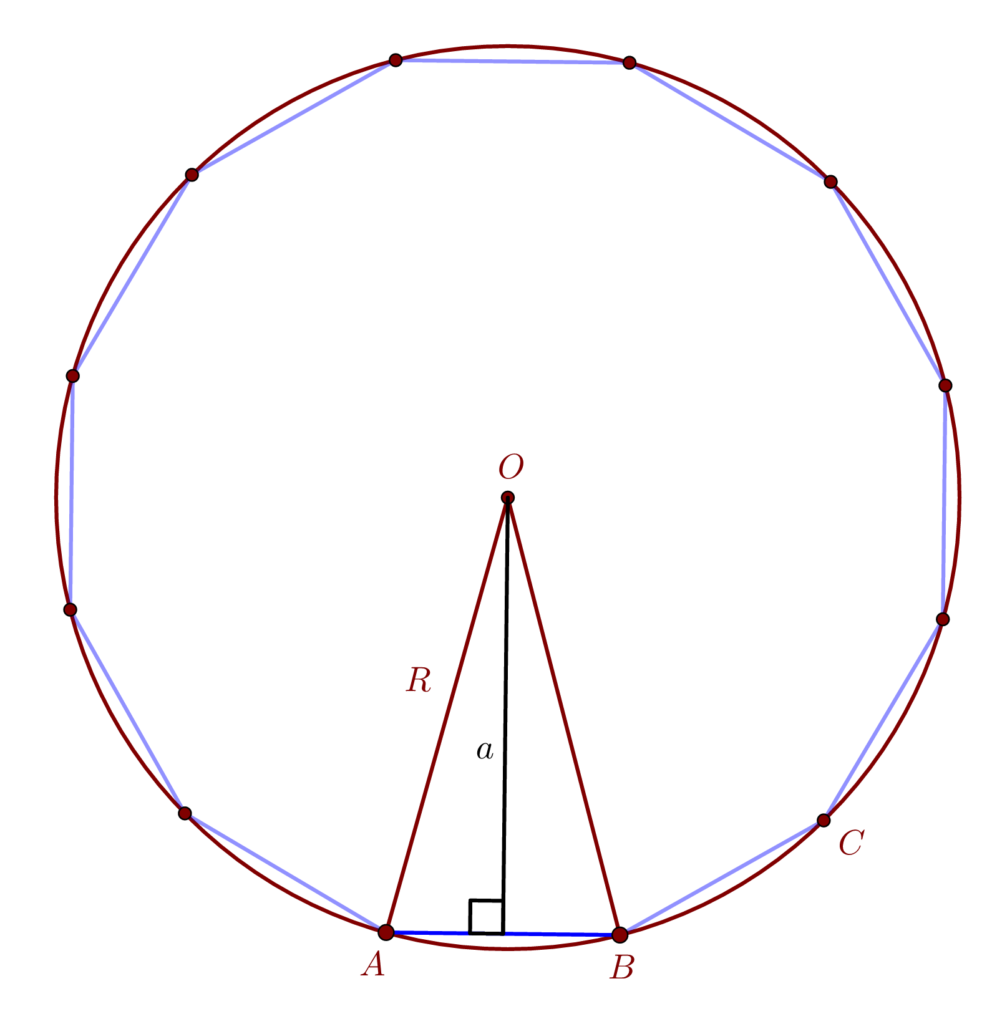
Distanța de la centrul cercului la laturile poligonului regulat se numește apotema poligonului. Vom nota cu a_n apotema poligonului de n laturi.

Articolul continuă pe pagina următoare

Măsura unui unghi interior

m(\measuredangle ABC) =\frac{180^\circ \cdot(n-2)}{n}

sau

m(\measuredangle ABC) =\frac{(n-2)\cdot \pi}{n}

Latura L_n :

L_n = 2\cdot R\cdot sin\frac{180^\circ}{n}

sau

L_n= 2\cdot R\cdot sin\frac{\pi}{n}

Apotema a_n

a_n=  R\cdot cos\frac{180^\circ}{n}

sau

a_n=R\cdot cos\frac{\pi}{n}

Aria unui poligon regulat cu n laturi

Aria se poate calcula în funcție de raza cercului circumscris ca:

S_n= \frac{1}{2}\cdot nR^2\cdot sin\frac{360^\circ}{n}

sau

S_n= \frac{1}{2}\cdot nR^2\cdot sin\frac{2\pi}{n}

Ne folosim de faptul că poligonul este împărțit în n triunghiuri isoscele cu vârful în centrul cercului. Acestora le calculăm aria folosindu-ne de cele două laturi egale și măsura unghiului dintre ele.

Aria se mai poate calcula și în funcție de perimetrul poligonului:

S_n=\frac{P_n\cdot a_n}{2}

Cum așa? Am împărțit poligonul în n triunghiuri cu arii egale, ca în cazul precedent. Acestea au baza egală cu latura poligonului și înălțimea – apotema acestuia.