Poligoanele înscrise în cerc – arii, laturi, apoteme

Patrulaterul înscris în cerc

Dacă un patrulater are toate vârfurile pe cerc se numește patrulater înscris în cerc.

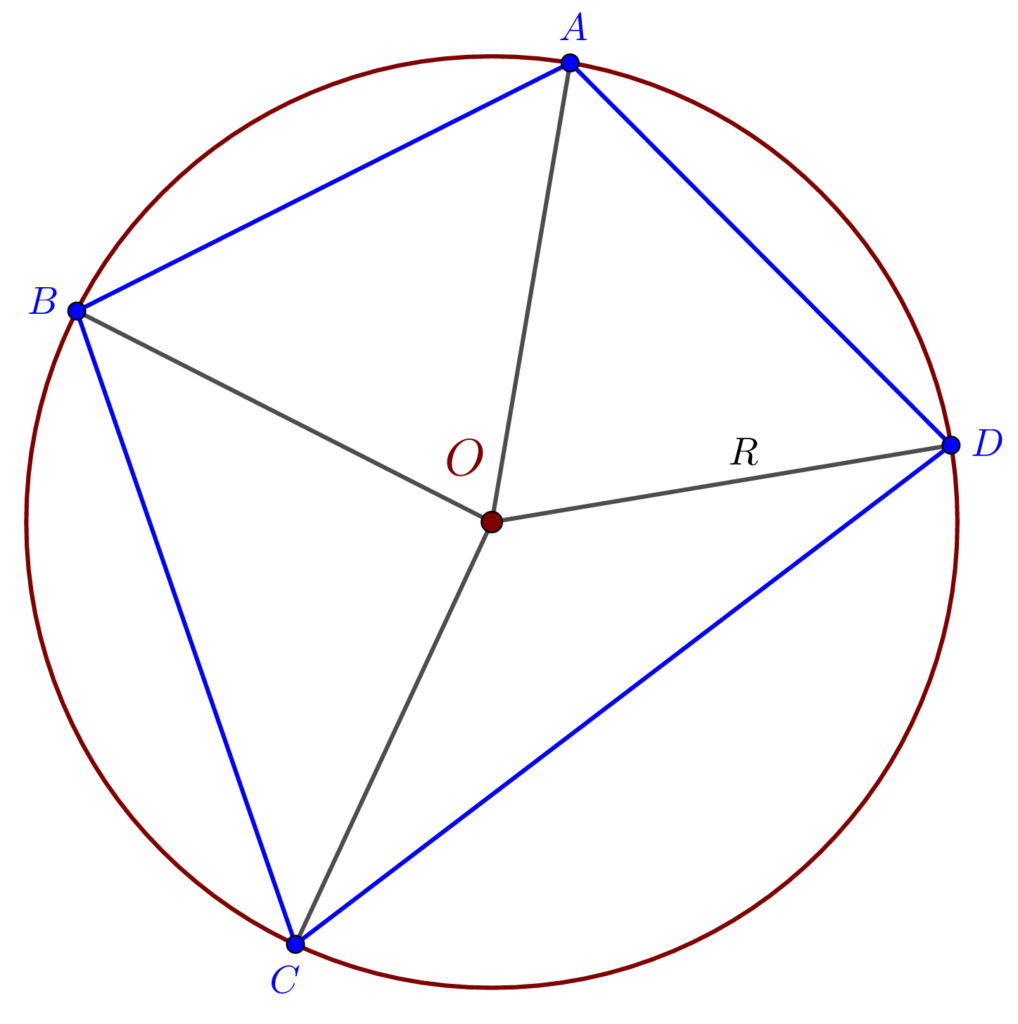
Consecință: – un patrulater înscris într-un cerc are vârfurile egal depărtate de centrul cercului (circumscris patrulaterului). Și reciproc, dacă un patrulater are vârfurile egal depărtate de un punct, atunci acest punct este centrul cercului circumscris, deci este patrulater inscriptibil.
Nu orice patrulater este inscriptibil.

Teoremă:
Un patrulater este inscriptibil dacă și numai dacă suma unghiurilor opuse este de 180^o (unghiurile opuse sunt suplementare).

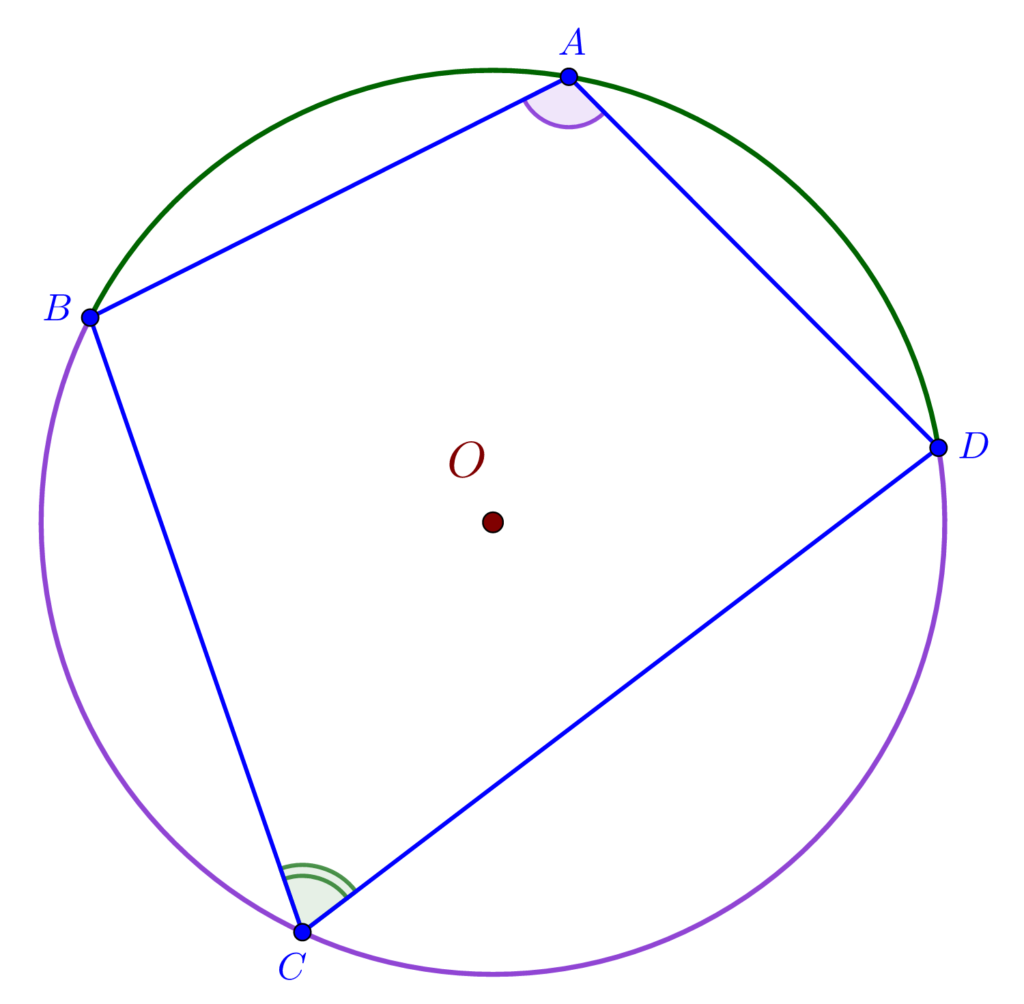
Această teoremă se demonstrează folosind proprietățile unghiului înscris în cerc.

Teoremă:
Un patrulater este inscriptibil dacă și numai dacă un unghi exterior este egal cu unghiul opus interior.

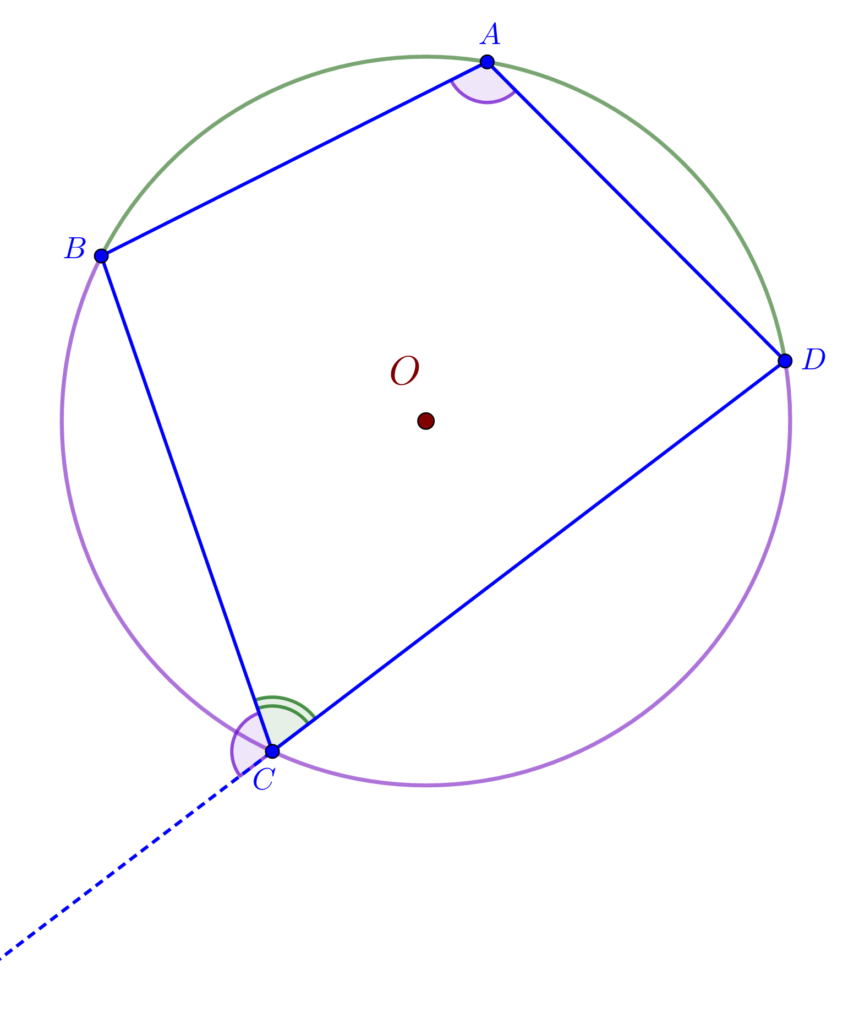
Teoremă:
Un patrulater este inscriptibil dacă și numai dacă unghiul format de o diagonală cu o latură este egal cu unghiul format de cealaltă diagonală cu latura opusă.

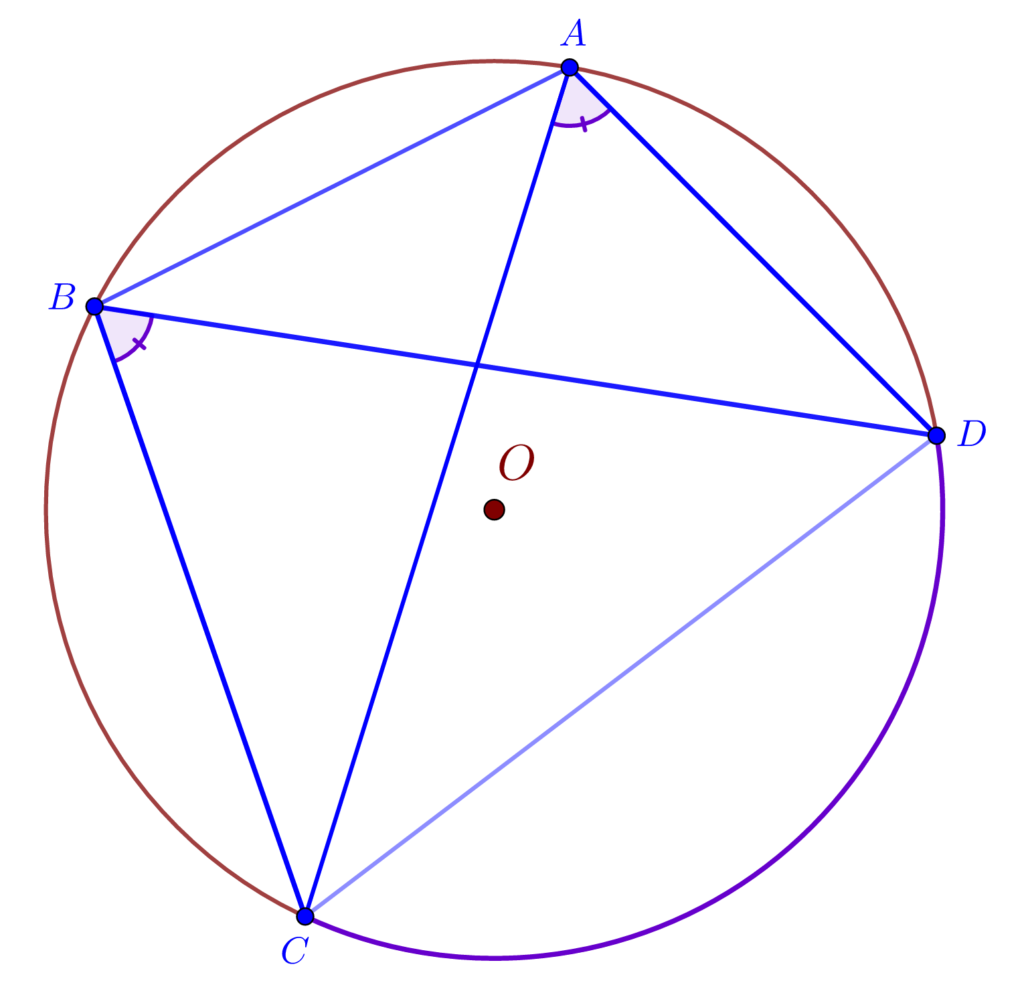
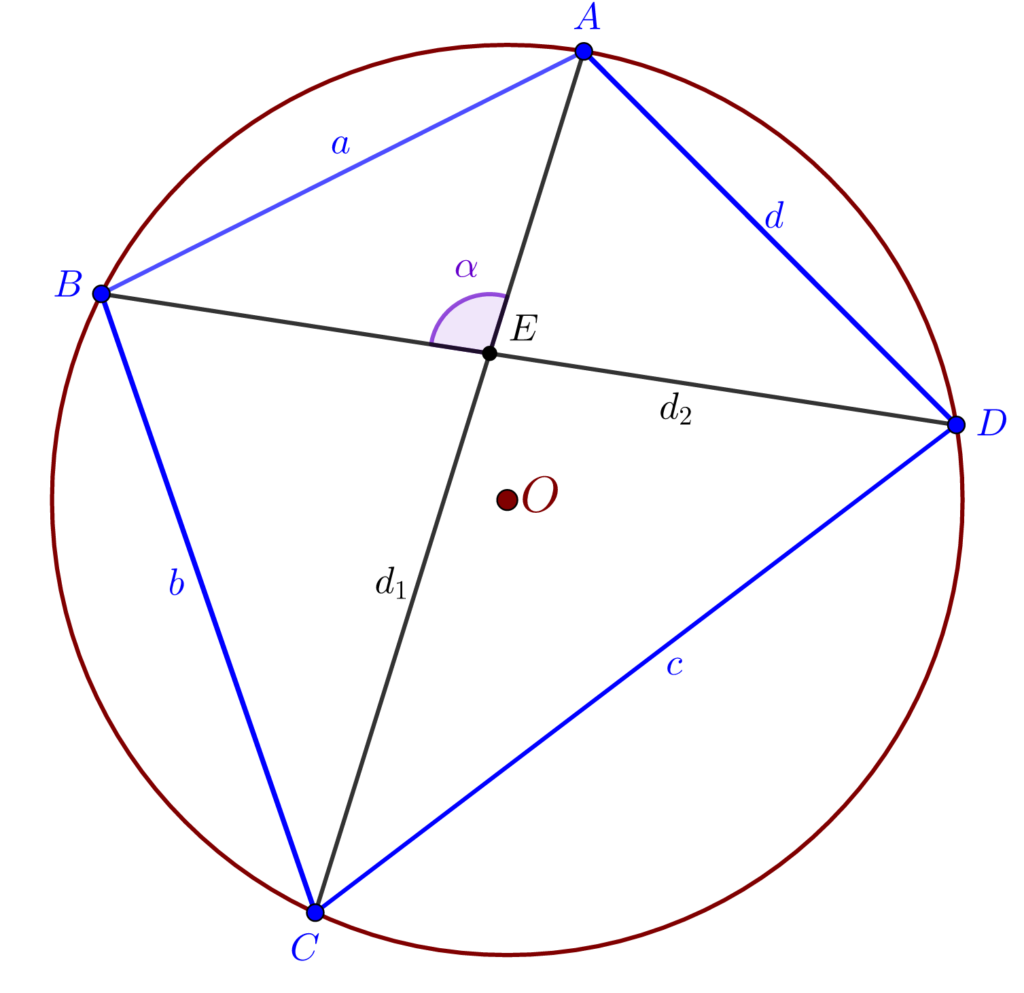
În continuare vom nota cu a, b, c respectiv d lungimile laturilor patrulaterului ABCD, cu d₁ respectiv d₂ lungimile diagonalelor, cu p semi-perimetrul și cu S aria patrulaterului. Considerând E punctul de intersecție al diagonalelor, vom nota cu α unghiul AEB.

Teorema lui Ptolemeu:
Un patrulater este inscriptibil dacă și numai dacă produsul diagonalelor este egal cu suma produselor laturilor opuse.

AC \cdot BD =AB \cdot CD +BC \cdot DA

sau

\\d_1\cdot d_2=a\cdot c+b\cdot d

Teorema a doua a lui Ptolemeu:
Fie ABCD un patrulater inscriptibil atunci are loc egalitatea:

\frac{AC}{BD} = \frac{BA\cdot AD+BC\cdot CD}{AB\cdot BC+AD\cdot DC}

sau

\frac{d_1}{d_2} = \frac{a\cdot d+b\cdot c}{a\cdot b+c\cdot d}

Aria patrulaterului inscriptibil:

S = \sqrt[]{(p-a)\cdot(p-b)\cdot(p-c)\cdot(p-d)}\\\;\\p = \frac{a+b+c+d}{2}

S=\frac{d_1\cdot d_2\cdot sin(\alpha)}{2}

Patrulatere particulare inscriptibile:

• dreptunghiul
• pătratul
• trapezul isoscel.

Patrulatere particulare neinscriptibile:

• paralelogramul
• rombul,
• trapezul oarecare
• trapezul dreptunghic

[the_ad_group id=”103″]