Poligonul este figura geometrică plană formată de o linie frântă închisă. Denumirea sa provine, ca a multor noțiuni geometrice, din limba greacă, însemnând „multe” (polus πολυς) „colțuri” (gonia γωνιά) . Poligoanele înscrise în cerc sunt acele poligoane ale căror vârfuri se află pe un cerc.
Din poligoanele simple, care nu se auto-intersectează, menționăm poligonul:
– convex: – Dacă prelungim oricare din laturile unui poligon convex, poligonul se află în întregime de aceeași parte a dreptei respective Toate unghiurile interioare ale poligonului convex sunt mai mici de 180o.
– concav: – Spre deosebire de poligonul convex, aici există o latură, cel puțin, a cărei prelungire taie suprafața poligonului. Există cel puțin un unghi interior a cărui măsură este mai mare de 180o.
Teoremă:
Suma măsurilor unghiurilor unui poligon convex cu n laturi, U, este:
U = (n-2)\cdot180^\circ
sau
U = (n-2)\cdot\pi
[the_ad_group id=”104″]
Poligonul înscris în cerc
Dacă un poligon are toate vârfurile pe cerc se numește poligon înscris în cerc, iar cercul este circumscris poligonului. Spunem că vârfurile poligonului sunt conciclice. Mai multe dintre proprietățile unghiurilor înscrise și arcelor de cerc se dovedesc foarte utile în demonstrarea proprietăților poligoanelor înscrise în cerc.
Triunghiul înscris în cerc
Triunghiul înscris în cerc are vârfurile situate pe cerc. Orice triunghi este inscriptibil. Centrul cercului circumscris triunghiului este punctul de intersecție al mediatoarelor.
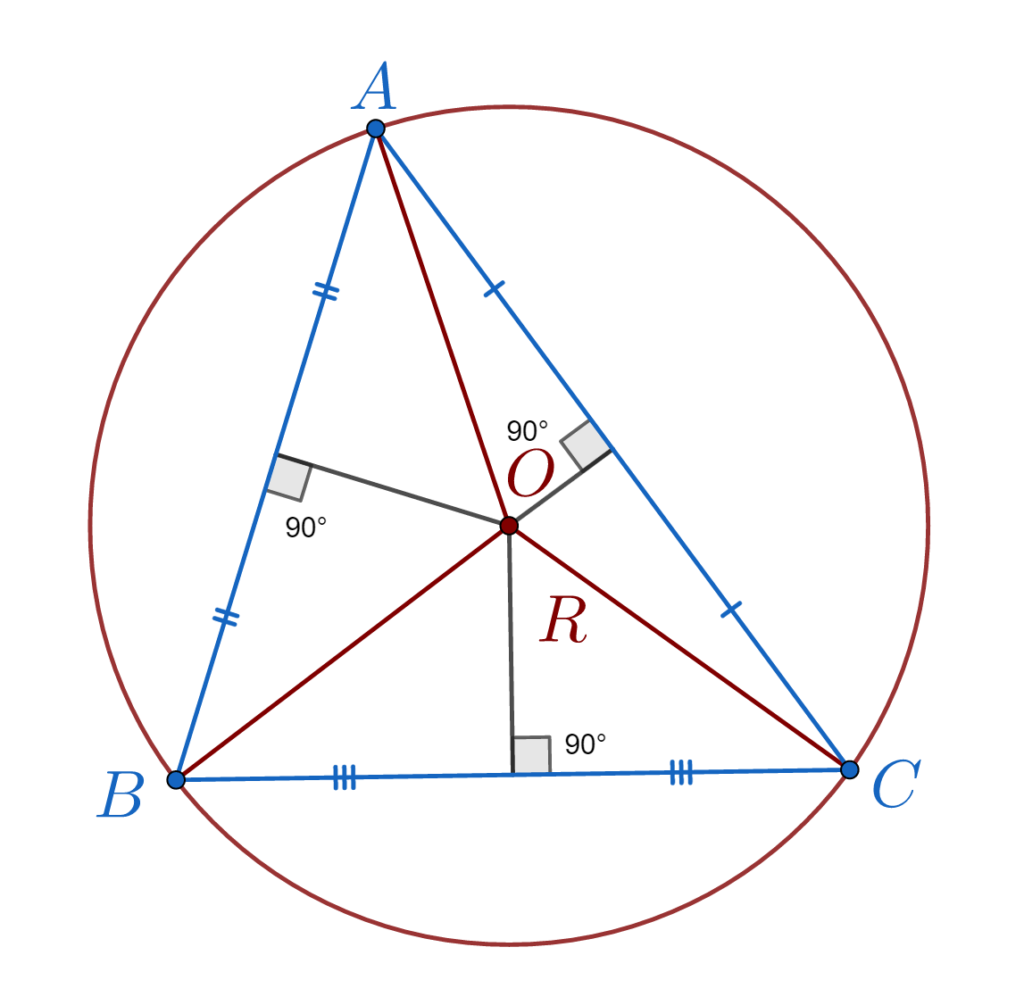
Raza cercului circumscris unui triunghi oarecare poate fi calculată, cunoscând măsurile laturilor și unghiurile sau suprafața triunghiului.
Articolul continuă pe pagina următoare



