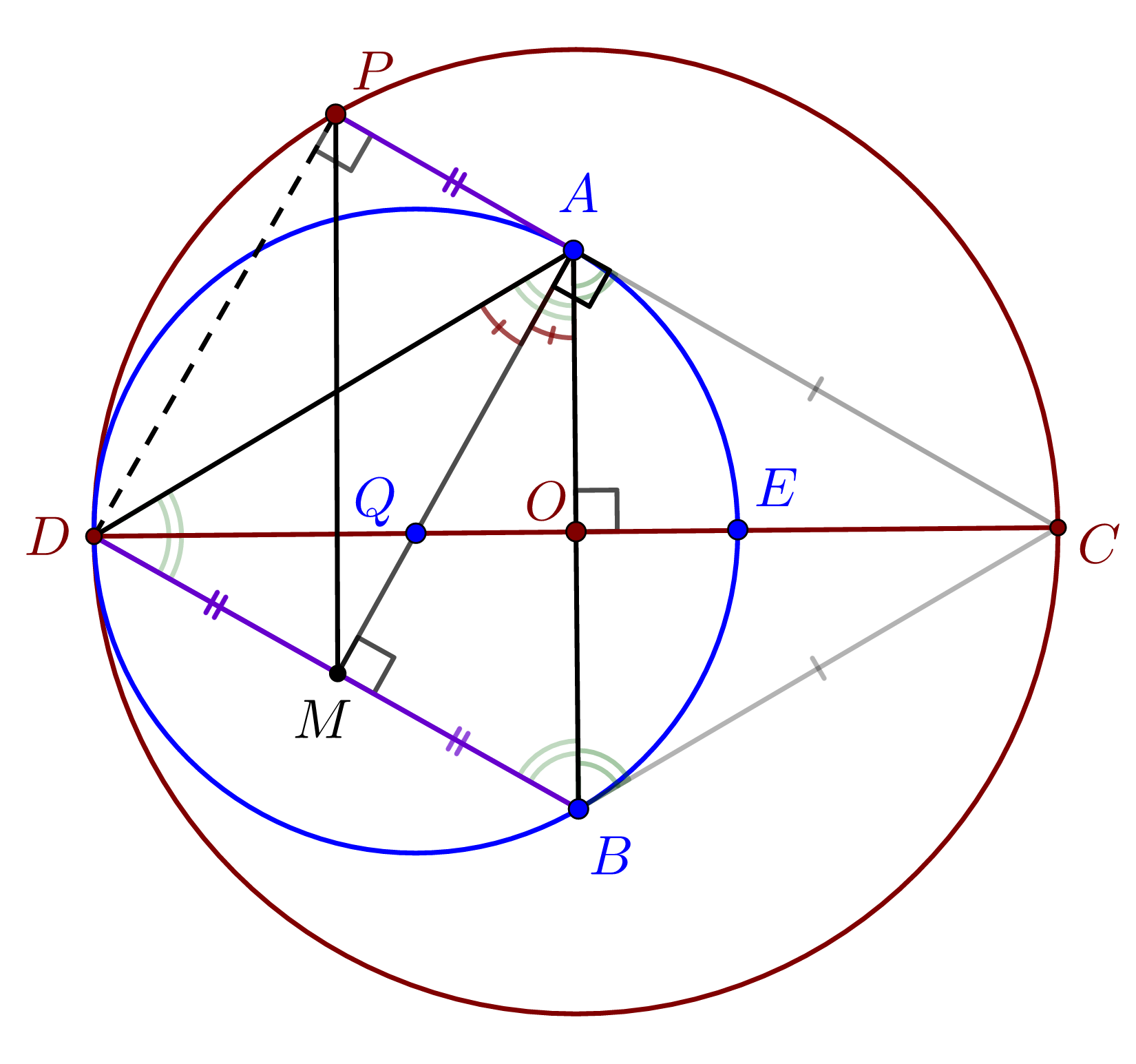
Știm că DAB este un triunghi înscris în cercul C(Q) si CA este o semi tangentă în A, atunci măsura unghiului CAB este egală cu măsura unghiului ADB.
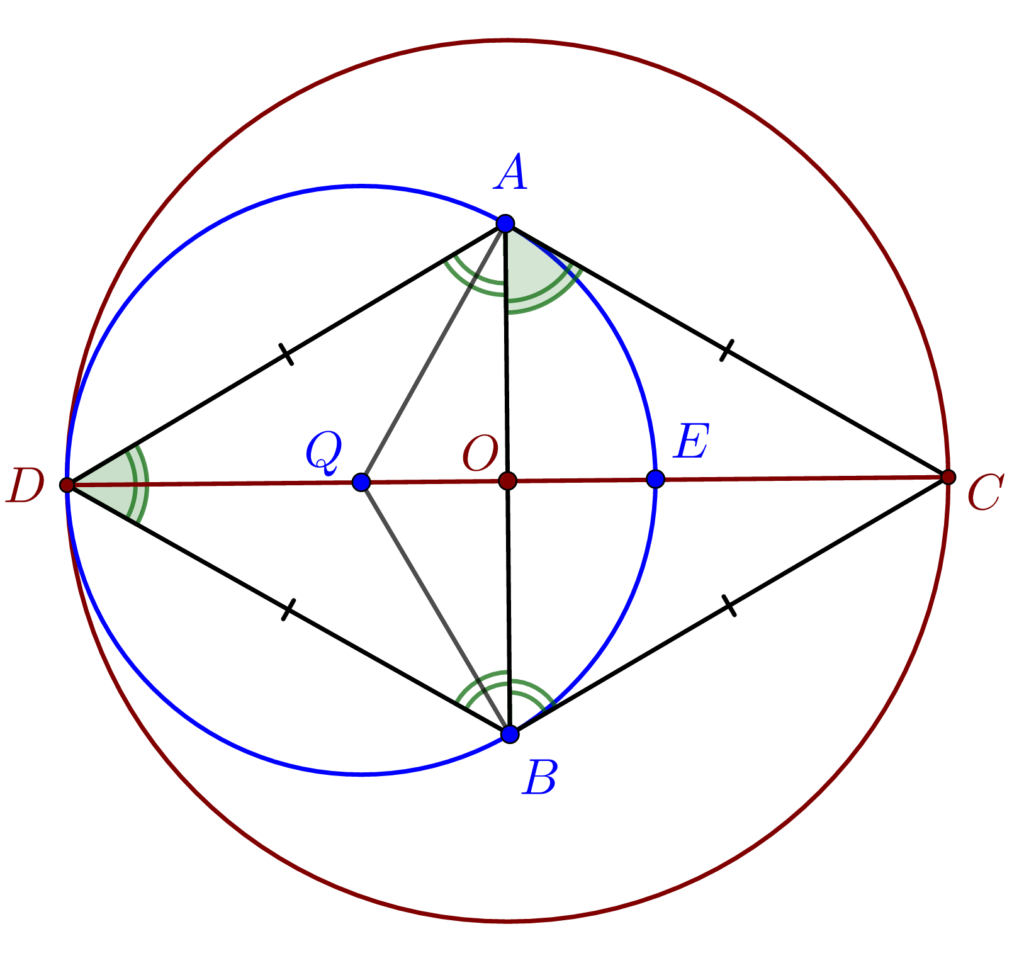
\left.
\begin{array}{ll}
CA\;tangentă\; la\;C(Q)\\
△ DAB\;înscris\;în\;C(Q)
\end{array}
\right \} \implies \\\;\\
\left.
\begin{array}{ll}
\implies m(\measuredangle ADB) = m(\measuredangle CAB) \\\;\\
\;\;\;\;\;\;\;\;\;am\;arătat\;că\;\\
\;\;\;\;\;\;\;\;\;m(\measuredangle DAO) = m(\measuredangle CAO)
\end{array}
\right \} \implies \\\;\\\implies m(\measuredangle ADB) = m(\measuredangle DAB) \implies \\\;\\\implies △ DBA\; isoscel \implies \\\;\\\left.
\begin{array}{ll}\implies [DB]\equiv[AB]\\
\;\;\;\;\;\;\;\;\;am\;arătat\;că\;\\ \;\;\;\;\;\;\;\;\;[DB]\equiv[BC]\\
\;\;\;\;\;\;\;\;\;[AC] \equiv [BC] \\
\end{array}
\right \} \implies \\\;\\\implies [AC]\equiv[BC]\equiv[AB]\implies \\\;\\\implies △ ABC △ echilateral
Pentru a demonstra punctul b)
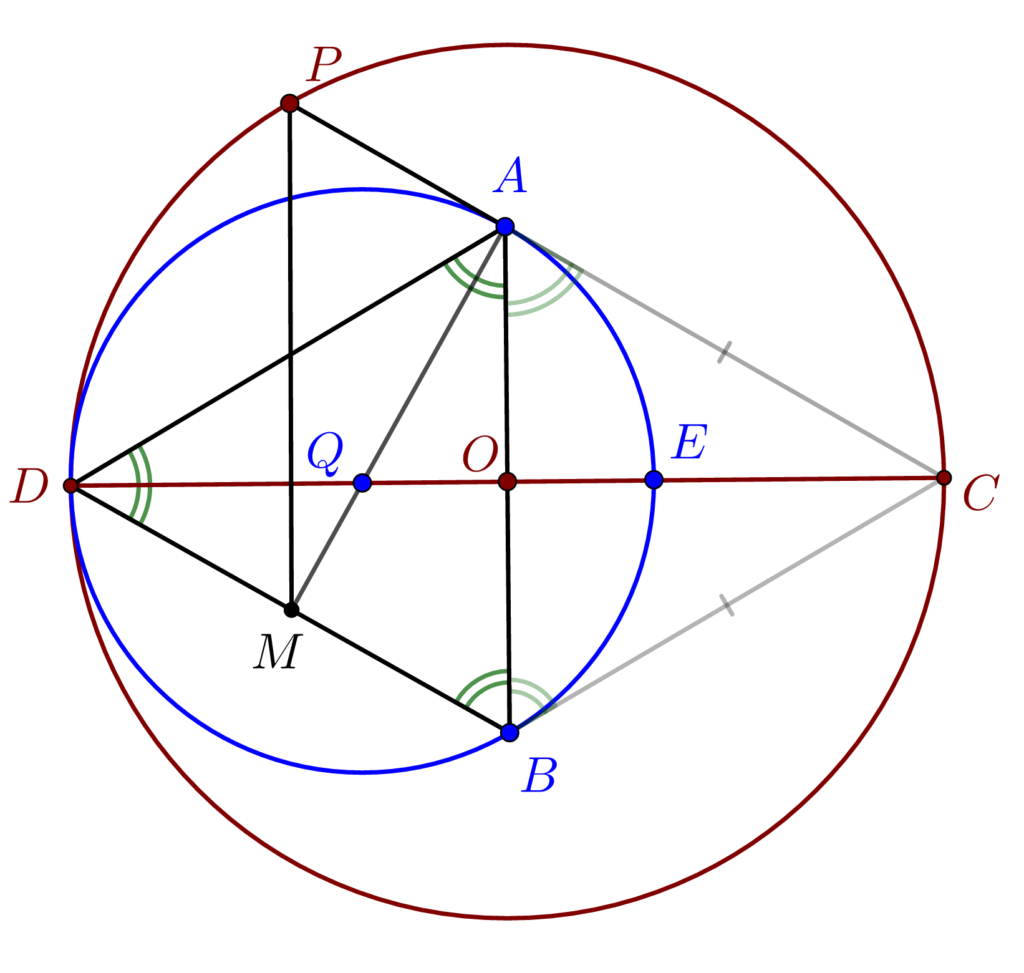
Știm că într-un triunghi echilateral liniile importante coincid (bisectoarele sunt și mediane și înălțimi). Arătăm că AM este bisectoare deci va fi și mediană și înălțime.
am\;arătat\;că\; \\
\left\{
\begin{array}{ll}
[DB]\equiv[BC]\\
[DA] \equiv [AC] \\
[AB]\equiv[BC]\equiv[AC]\\
\\
\end{array}
\right \} \implies \\\ \implies [AB]\equiv[DB]\equiv[DA]\implies \\\;\\\implies △ DBA △ echilateral
\\am\;arătat\;și\;că\;
△ ABC △ echilateral\\\;\\
\left.
\begin{array}{ll}
QA\perp AC (tangentă)\\\;\\
m(\measuredangle CAB) = 60^\circ \\\;\\
m(\measuredangle QAC) = m(\measuredangle QAO) + m(\measuredangle OAC)
\end{array}
\right \}\implies\\\;\\\implies m(\measuredangle QAO) = 90^\circ -60^\circ \implies\\\;\\
\left.
\begin{array}{ll}
\implies m(\measuredangle QAO) = 30^\circ \\
m(\measuredangle DAB) = 60^\circ (△ DBA △ echilateral)
\end{array}
\right \}\implies\\\;\\\implies m(\measuredangle DAM) = 60^\circ -30^\circ\implies\\\;\\\implies m(\measuredangle DAM) = m(\measuredangle BAM) \implies\\\;\\\implies AM\;bisectoare\;în\;△ echilateral\implies \\\;\\\implies AM\;înălțime\; și\; mediană\implies \\\;\\
În continuare vom arăta că PDMA este dreptunghi. MA este perpendiculară pe AC deoarece QA este rază și AC este tangentă; am arătat ca AM este înălțime în triunghiul DAB. De asemenea știm că un unghi înscris într-un semicerc are măsura de 900, observăm că DPC este un unghi înscris în semicerc, deci va avea 900 astfel PDMA este dreptunghi.
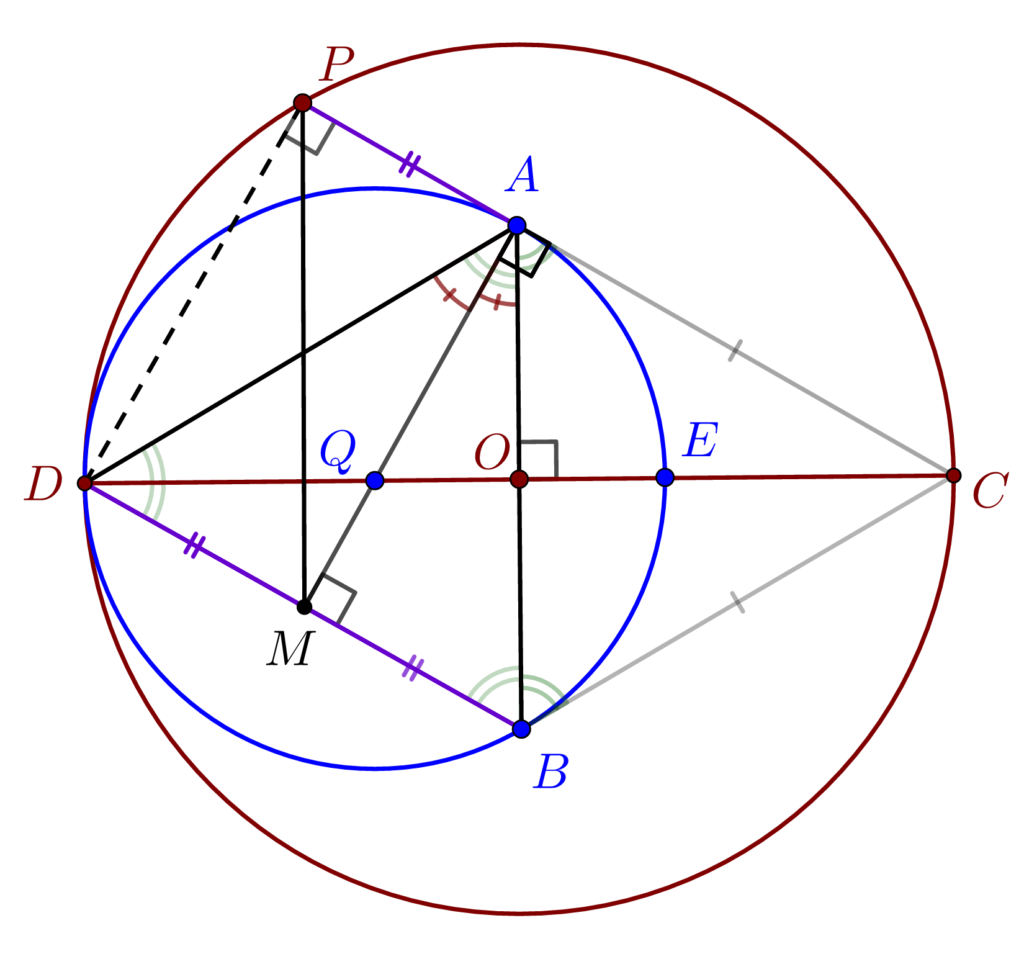
\left.
\begin{array}{ll}
P \in C(O)\\
DC\;diametru\;în\; C(O)
\end{array}
\right \}\implies\\\;\\\\\implies m(\measuredangle DPA) = 90^\circ
\implies\\\;\\
\left.
\begin{array}{ll}
\implies DP\perp PC\\
AM \perp BD \;(AM\;înălțime)\\
AM \perp PC
\end{array}
\right \}\implies\\\;\\\implies PDMA \;dreptunghi \implies\\\;\\
\left.
\begin{array}{ll}
\implies [PA]\equiv[DM]\\
\;\;\;\;\;\;\;\;\;[DM]\equiv[MB] (\;AM\;mediană\;)
\end{array}
\right \}\implies\\\;\\
\left.
\begin{array}{ll}
\implies [PA]\equiv[MB] \\\;\\
\left.
\begin{array}{ll}
AM\perp DB\\
AM\perp CP
\end{array}
\right \}\implies DB \parallel PC
\end{array}
\right \}\implies\\\;\\MBAP\;paralelogram\implies\\\;\\
\left.
\begin{array}{ll}
\implies
AB \parallel PM\\
\;\;\;\;\;\;\;\;\;AB\perp CD
\end{array}
\right \}\implies\\\;\\\implies PM \perp CD[the_ad_group id=”102″]
Pages: 1 2