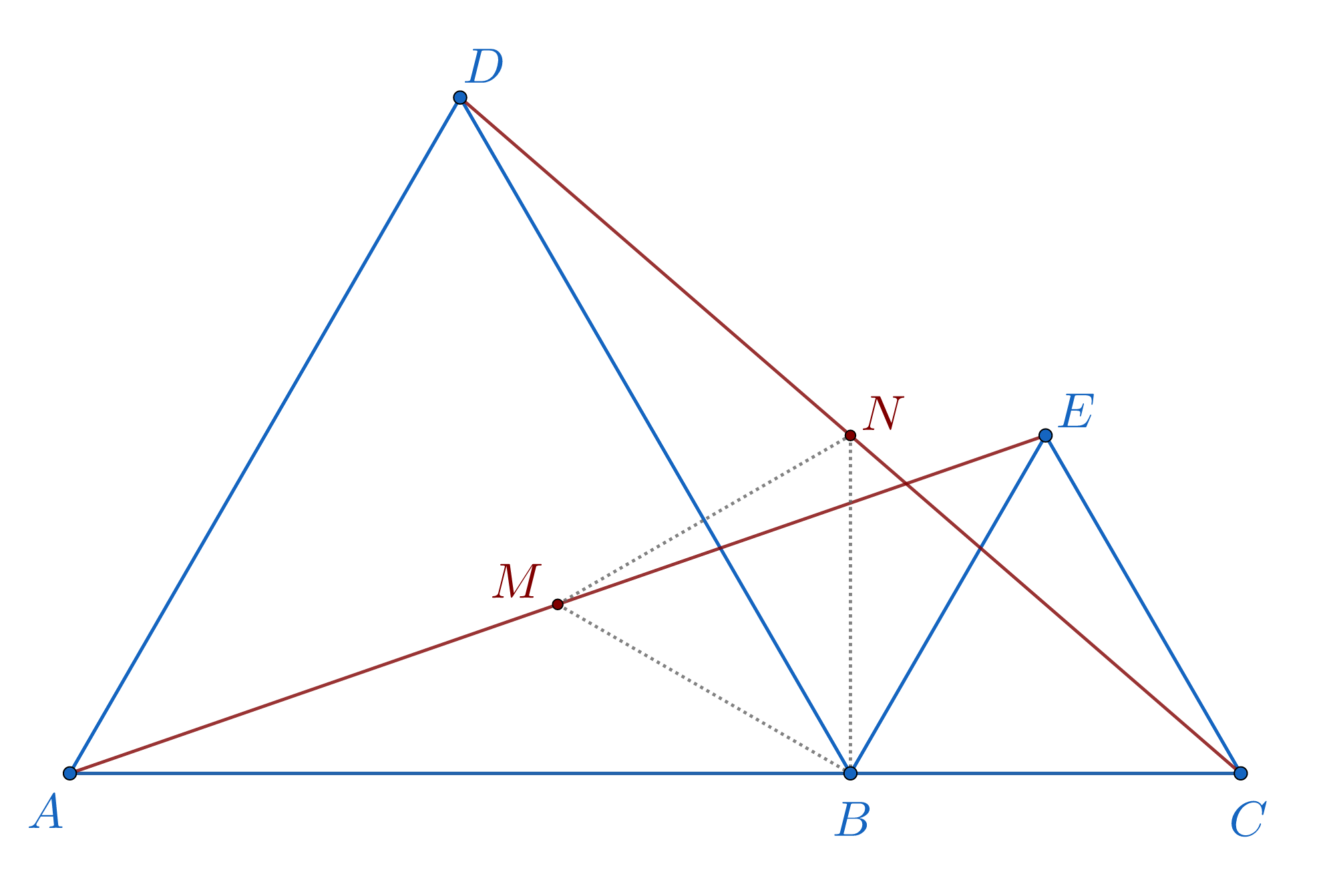
În figura de mai jos, atât triunghiul ABD cât și triunghiul BCE sunt echilaterale. Punctul B aparține lui (AC), AB = 12 cm și BC = 6 cm. Punctele M și N sunt mijloacele segmentelor AE, respectiv CD.
a) Calculeaza lungimea segmentului AE.
b) Determină măsura unghiului MBN.
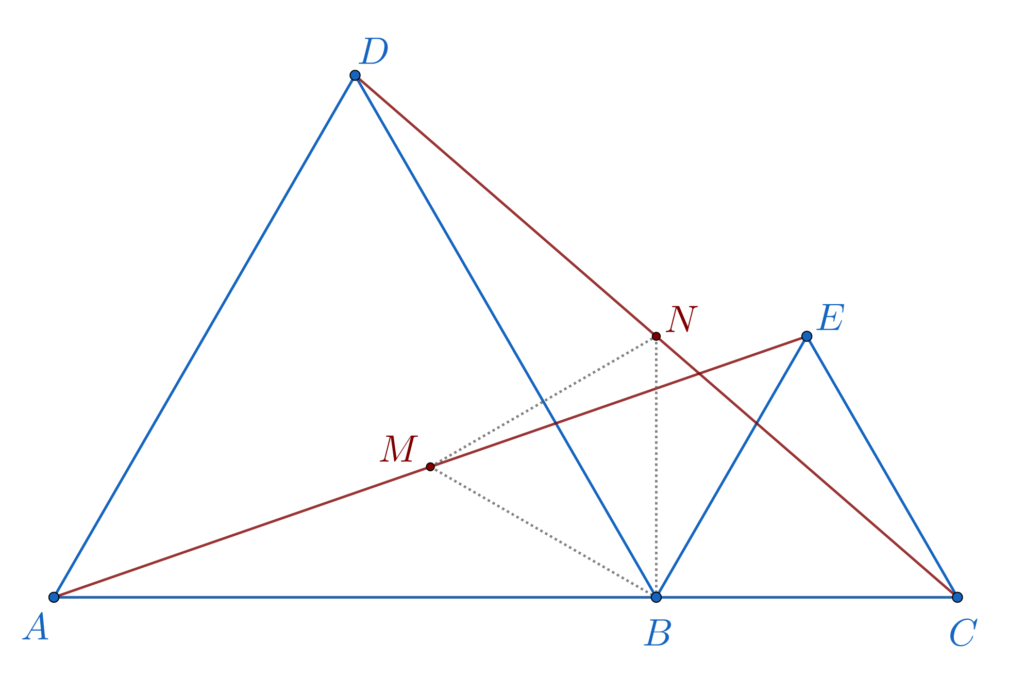
Înainte de rezolvarea acestei probleme, puteți consulta și cele mai importante teoreme într-un triunghi oarecare.
a) Pentru a rezolva prima cerință construim înălțimea EF în triunghiul BCE și o calculăm. Apoi aplicăm teorema lui Pitagora în triunghiul AFE.
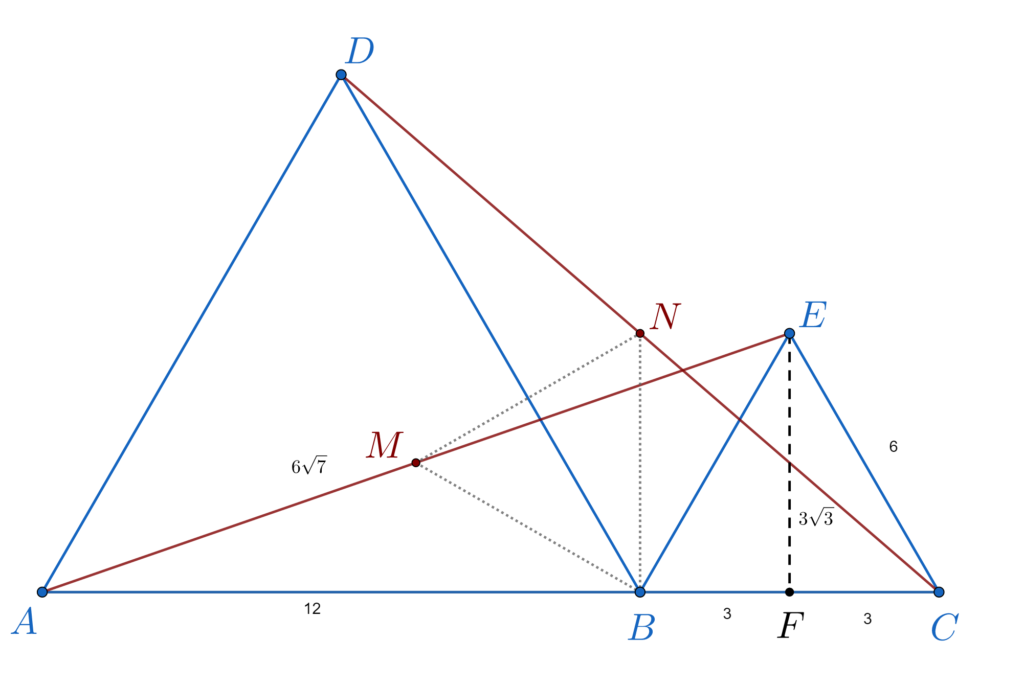
Pentru a afla EF aplicăm fie formula pentru a afla înălțimea fie o calculăm din teorema lui Pitagora în EFC (știm că înălțimea în triunghiul echilateral este și mediană, deci FC = 3 cm).
EF = \frac{6\cdot\sqrt[]{3}}{2}\implies EF =3\cdot\sqrt[]{3}După ce l-am aflat pe EF, aplicăm teorema lui Pitagora în triunghiul AEF.
\left.
\begin{array}{ll}
BF = 3\\
AB = 12\\
AF = AB + BF
\end{array}
\right \}
\implies\;\\\; \\\left.
\begin{array}{ll}
\implies AF = 15\\
\;\;\;\;\;\;\;\;EF =3\cdot\sqrt[]{3}\\\;\\
\;\;\;\;\;\;\;\;AE^2=AF^2+EF^2 \\
\end{array}
\right \}
\implies\;\\\; \\ \implies AE^2 = 15^2+(3\cdot\sqrt[]{3})^2\implies \\\;\\\implies AE^2=225 + 27\implies \\\;\\\implies AE^2=252\implies AE = 6\cdot\sqrt[]{7}b) Pentru a găsi răspunsul la al doilea punct punctul, arătăm mai întâi că triunghiurile ABE și DBC sunt congruente, M și N fiind mijloacele segmentelor AE respectiv DC; va rezulta că AM = DN; folosim aceasta pentru a demonstra că triunghiurile AMB și DNB sunt congruente. De aici obținem că măsura unghiului MBA este egală cu măsura unghiului NBD.

\left.
\begin{array}{ll}
m(\measuredangle ABE) = 180^{\circ}- m(\measuredangle CBE)\\\;\\
m(\measuredangle DBC) = 180^{\circ}-m(\measuredangle DBA)\\\;\\
m(\measuredangle CBE) = m(\measuredangle DBA) = 60^{\circ}
\end{array}
\right \} {\implies}\;\\\;\\
\left.
\begin{array}{ll}
\implies m(\measuredangle ABE) = m(\measuredangle DBC) =120^{\circ}\\\;\\
\;\;\;\;\;\;\;\;AB =DB\\\;\\
\;\;\;\;\;\;\;\;BE = BC\\
\end{array}
\right \} \overset{LUL}{\implies}\;\\\;\\ \overset{LUL}{\implies}△ABE \equiv △ DBC\implies \\\;\\\implies
\left\{
\begin{array}{ll}
m(\measuredangle EAB) = m(\measuredangle BDC) \\
AE = DC\\
\end{array}
\right.\\\;\\
\left.
\begin{array}{ll}
AE = DC\\
M\;este\;mijlocu\; lui\; AE\\
N\;este\;mijlocu\; lui\; DC\\
\end{array}
\right \}{\implies}\;\\\;\\
\left.
\begin{array}{ll}
\implies AM = DN \\
\;\;\;\;\;\;\;\;m(\measuredangle EAB) = m(\measuredangle BDC)\\
\;\;\;\;\;\;\;\;AB = DB
\end{array}
\right \} \overset{LUL}{\implies}\;\\\; \\\overset{LUL}{\implies}△ABM \equiv △ DBN\implies \\\;\\\implies
m(\measuredangle NBD) = m(\measuredangle MBA)\\

Măsura unghiului MBN este egală cu suma măsurilor unghiurilor MBD și DBN, însă unghiul NBD este egal cu unghiul MBA, iar suma unghiurilor DBM și MBA este egală cu măsura unghiului DBA, 60o.
\left.
\begin{array}{ll}
m(\measuredangle MBN) = \\m(\measuredangle DBN) +m(\measuredangle DBM) \\\;\\
m(\measuredangle DBN) = m(\measuredangle MBA)\\
\end{array}
\right \}\implies\\\;\\\implies m(\measuredangle MBN) = \\= m(\measuredangle DBM) +m(\measuredangle MBA) \implies\\\;\\
\left.
\begin{array}{ll}
\implies m(\measuredangle MBN) = m(\measuredangle DBA) \\
\;\;\;\;\;\;\;\;\;m(\measuredangle DBA) = 60 ^\circ
\end{array}
\right \}\implies\\\;\\\implies m(\measuredangle MBN) = 60 ^\circ
[the_ad_group id=”102″]