Triunghiul oarecare – cele mai importante 16 teoreme

8. Teorema lui Ceva

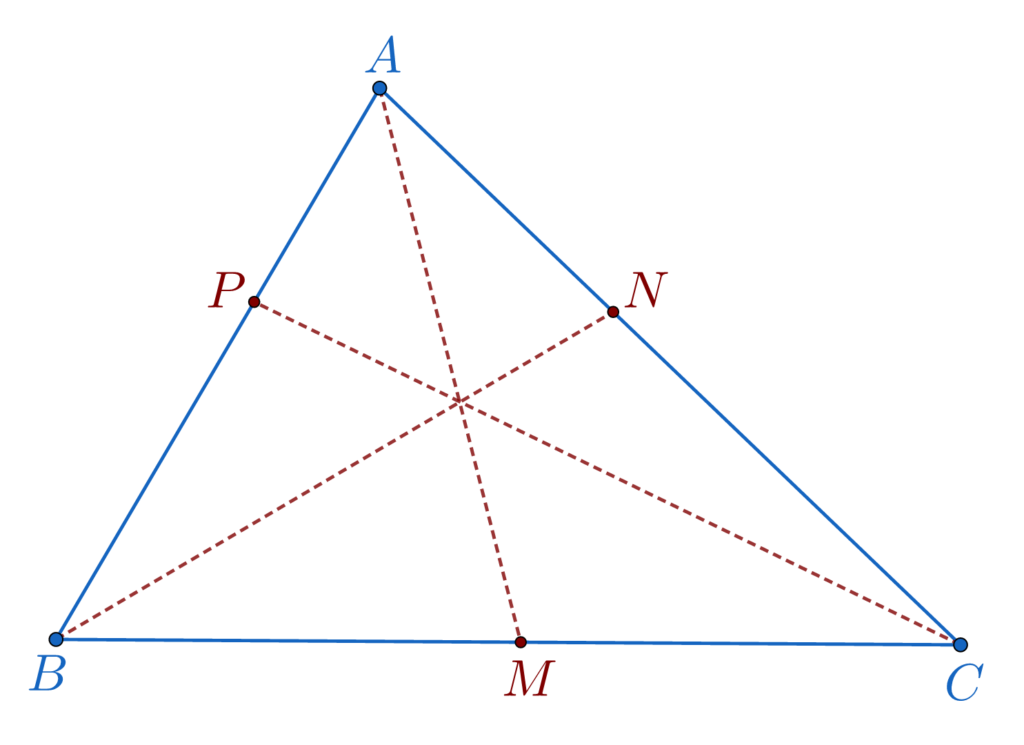
Dacă pe laturile unui triunghi ABC luăm trei puncte M, N, P (M pe latura BC, N pe latura AC și P pe latura AB) astel încât:

\frac{AP}{PB}\cdot\frac{BM}{MC}\cdot\frac{CN}{NA}=1

atunci dreptele AM, BN și CP sunt concurente.

9. Inegalitățile triunghiului

Cu segmentele a, b, c se poate construi un trunghi dacă și numai dacă:

a < b+c,\; b < c+ a, \; c < b+a\\
sau\\
|b-c|< a < b+c

10. Proprietatea unghiului opus laturii

Într-un triunghi cu două laturi neegale, laturii cu lungimea mai mare i se opune unghiul mai mare și reciproc.

11. Proprietatea centrului de greutate

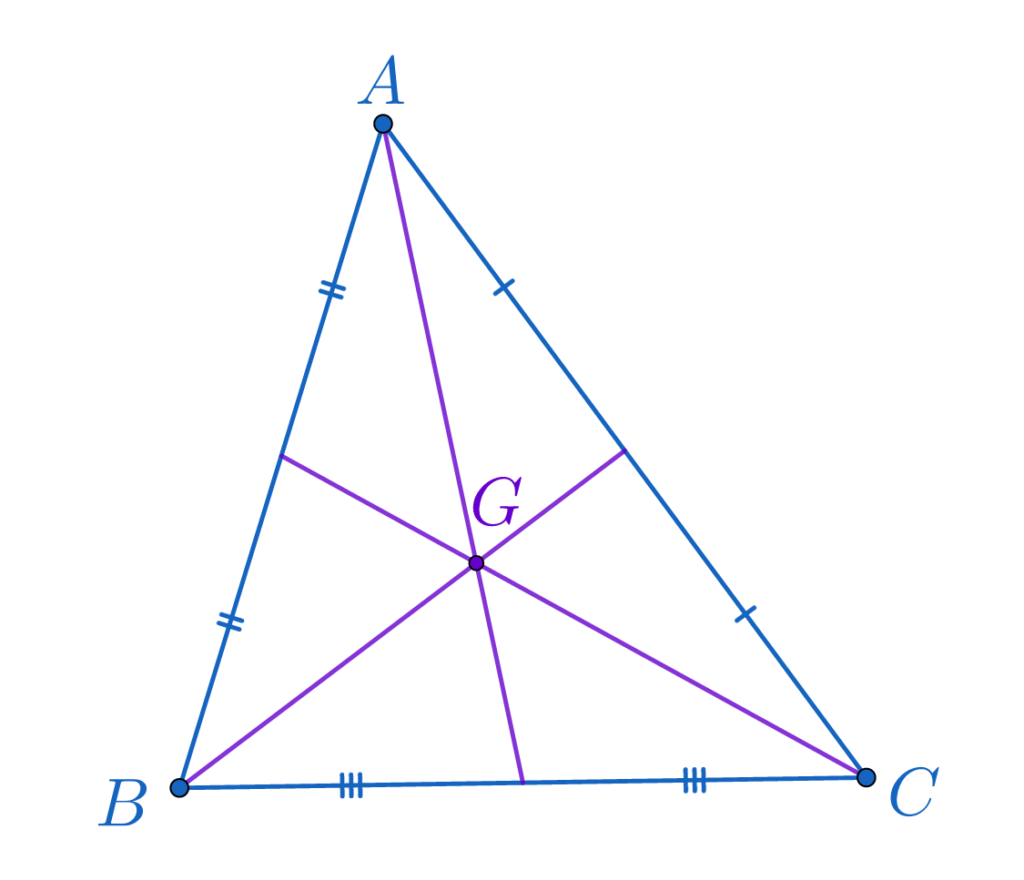
Centrul de greutate se află la o treime de bază și două de vârf.

O consecință imediată a proprietății anterioare, este aceea că fiecare mediană împarte triunghiul în alte două triunghiuri de arii egale.

12. Teorema lui Pitagora Generalizată

Fie triunghiul oarecare ABC, atunci se verifică relația:

a^2=b^2+c^2 -2\ bc \cdot cosA

13. Dreapta lui Euler

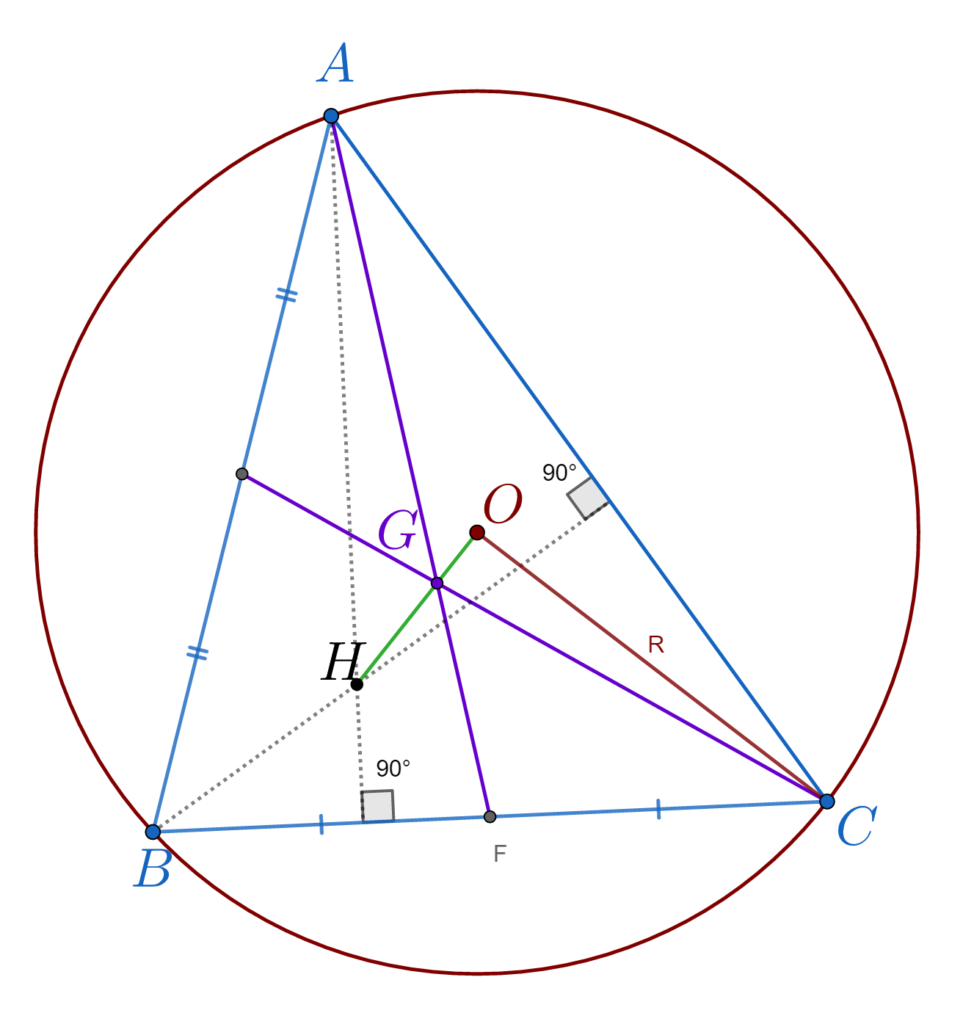
Dacă ABC este un triunghi oarecare și O centrul cercului circumscris, G centrul de greutate si H ortocentrul triunghiului atunci punctele H, G și O sunt colineare, ele se găsesc pe dreapta lui Euler și avem:

HG = 2\cdot GO

14. Cercul lui Euler (cercul celor 9 puncte)

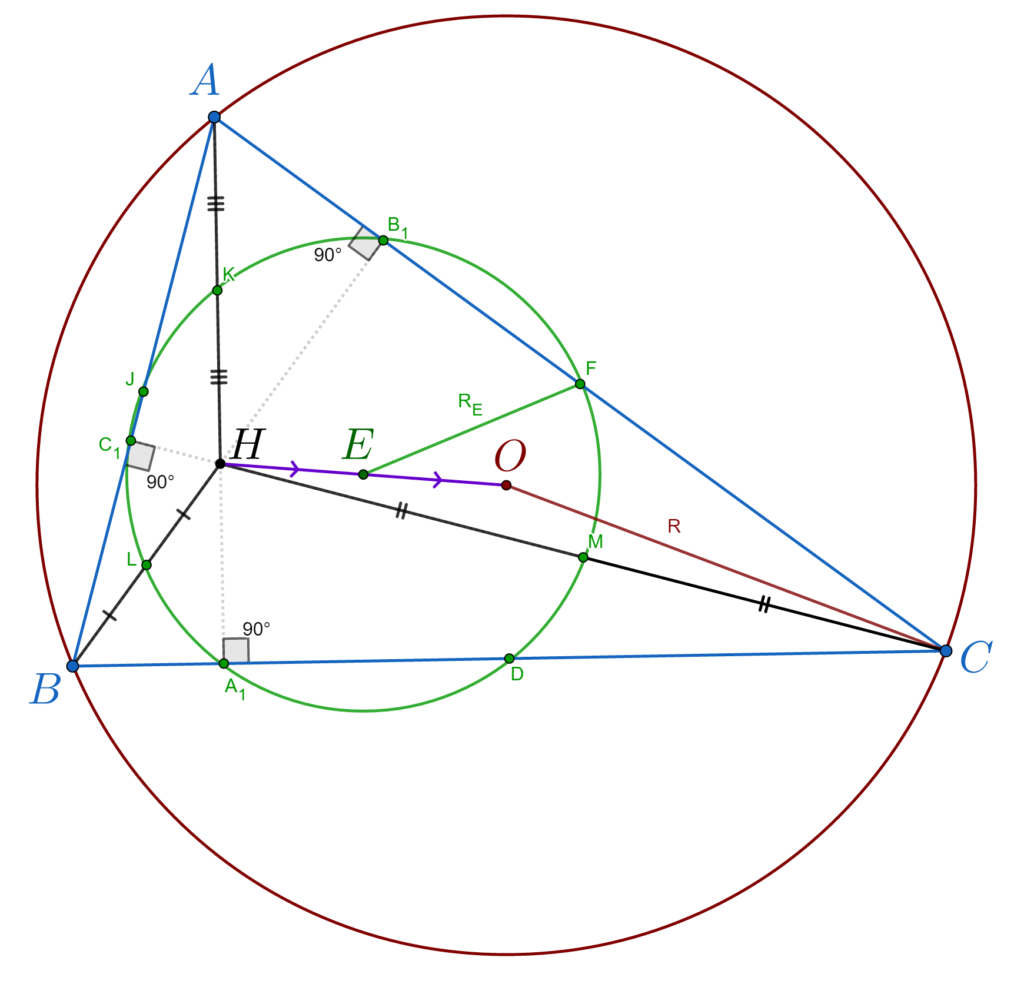
Dacă ABC este un triunghi oarecare, atunci picioarele înălțimilor (A₁, B₁, C₁), mijloacele laturilor (D, F și J) și mijloacele segmentelor AH, BH, CH (K, L, M), unde H este ortocentrul, triunghiului sunt conciclice.

Raza cercului Euler este jumătatea razei centrul cercului circumscris.

Centrul cercului lui Euler se găsește pe dreapta lui Euler și coincide cu mijlocul segmentului determinat de ortocentru (H) și de cercul centrului circumscris triunghiului.

OH = \sqrt[]{R^2-8\cdot R^2\cdot cosA\cdot cosB\cdot cosC} \\\;\\\ sau \\\;\\OH = \sqrt[]{9R^2-(a^2+b^2+c^2)}

15. Teorema lui Euler

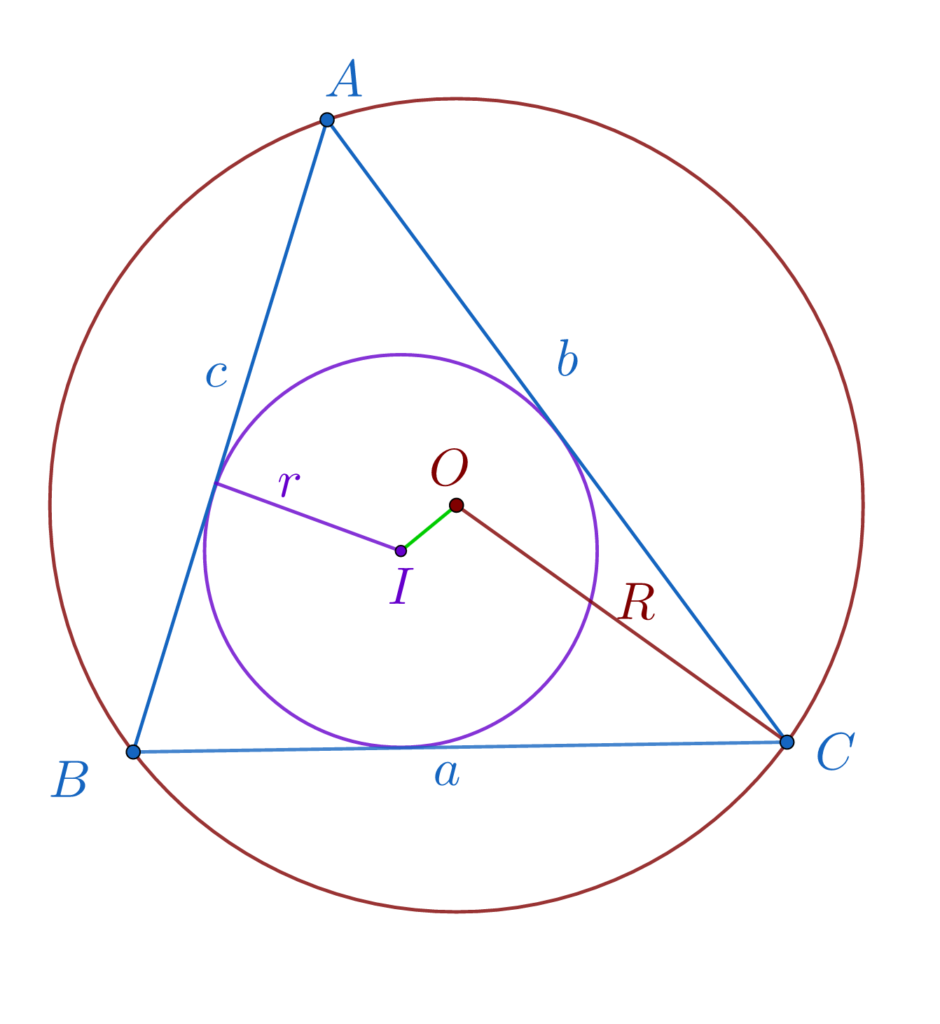
Distanța dintre centrul O al cercului circumscris unui triunghi și centrul I al cercului înscris în același triunghi este:

OI = \sqrt[]{R^2-2Rr}

16. Dreapta lui Simson

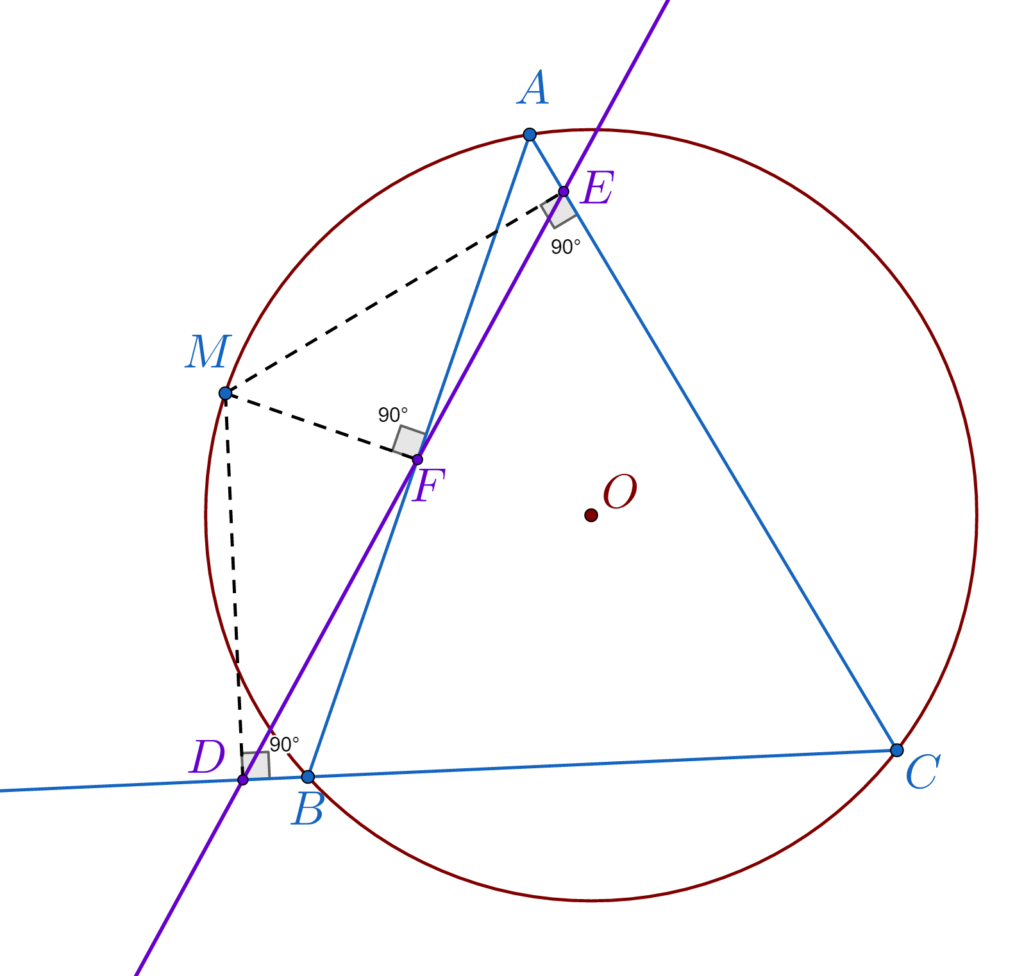
Dacă dintr-un punct M al cercului circumscris triunghiului ABC se coboară perpendicularele MD, MF, ME pe BC, AB și AC atunci punctele D, F și E sunt colineare.

[the_ad_group id=”102″]