Teoreme importante și relații în triunghi:
1. Suma unghiurilor unui triunghi
Suma unghiurilor unui triunghi este egală cu 1800.
O problemă rezolvată în care folosim această proprietate găsiți aici.
2. Măsura unghiului exterior
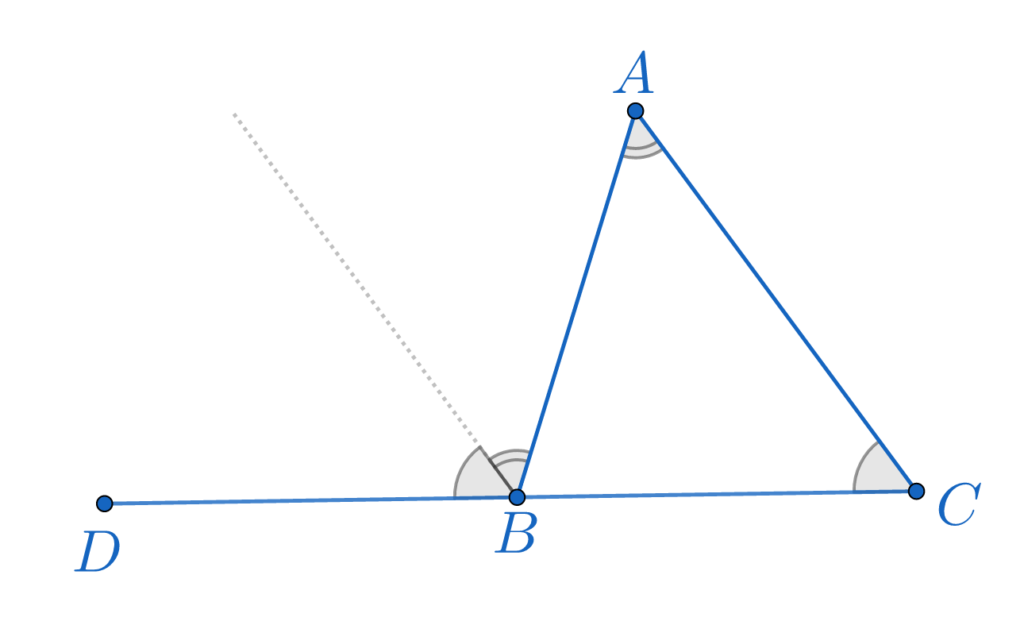
Un unghi exterior al unui triunghi este egal cu suma celor două unghiuri ale triunghiului care nu îi sunt alăturate.
m(\measuredangle ABD) = m(\measuredangle BAC) + m(\measuredangle ACB)
3. Teorema lui Thales:
O paralelă la una din laturile unui triunghi împarte celelalte două laturi în segmente proporționale.
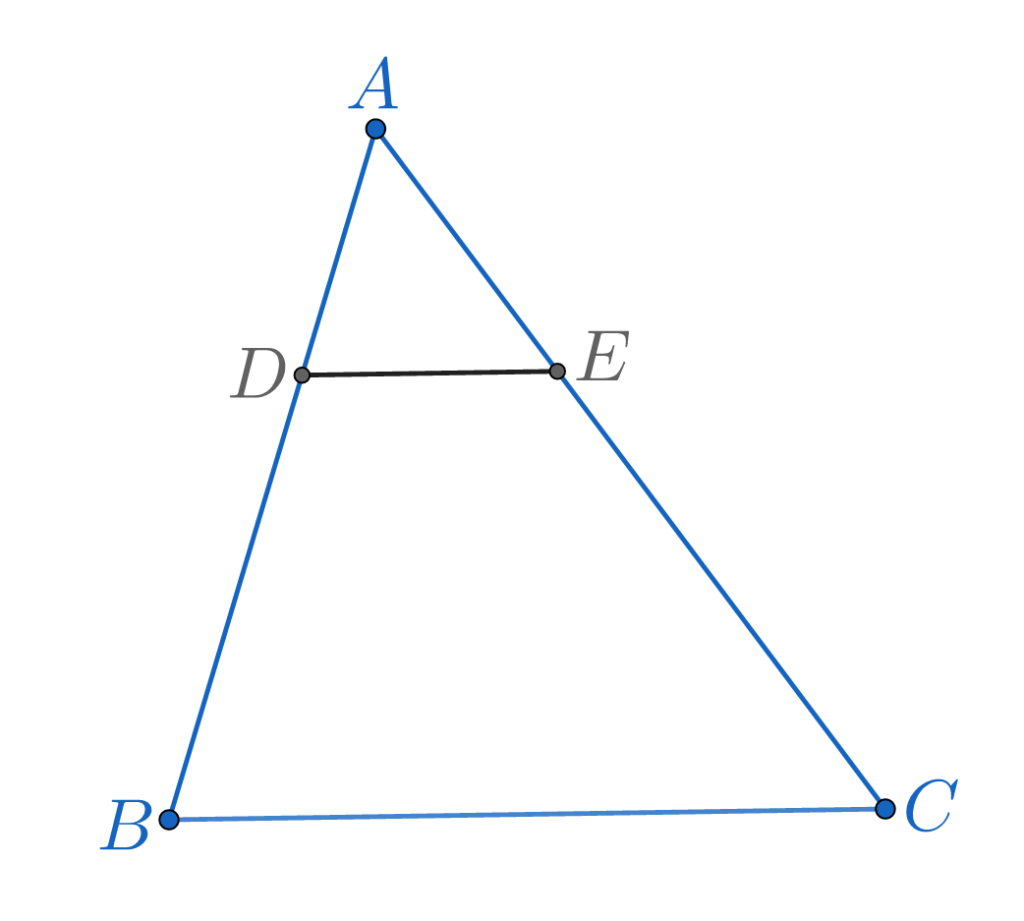
Fie triunghiul oarecare ABC și D un punct pe AB, iar E un punct pe AC astfel încât DE || BC atunci:
DE||BC \implies\frac{AD}{DB}=\frac{AE}{EC}4. Linia mijlocie
Segmentul care unește mijloacele a două laturi ale unui triunghi este paralel cu a treia latură și este egal cu jumătate din aceasta.
O problemă rezolvată în care folosim această proprietate găsiți aici.
5. Teorema bisectoarei:
Bisectoarele (interioară și cea exterioară) unui unghi dintr-un triunghi împart latura opusă în segmente proporționale cu celelalte două laturi.
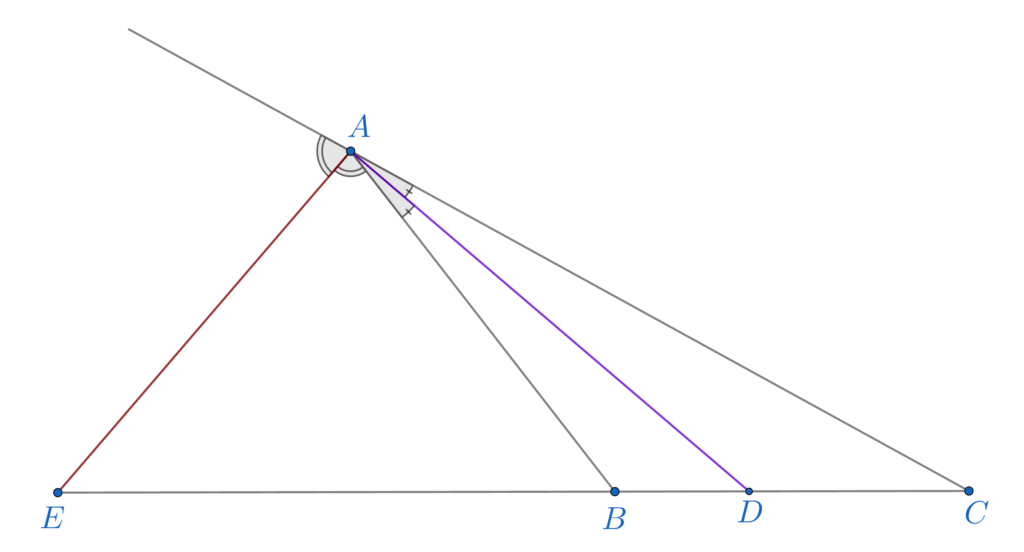
Fie triunghiul oarecare ABC, AD bisectoarea interioara unghiului BAC și AE bisectoarea exterioară unghiului BAC. Atunci:
\frac{AB}{AC}=\frac{BD}{DC}\\\:\\\frac{AB}{AC}=\frac{BE}{CE}[the_ad_group id=”103″]
6. Teorema lui Stewart
Dacă A, B și C sunt trei puncte colineare, în această ordine, iar O este un punct exterior dreptei pe care se află cele trei puncte atunci:
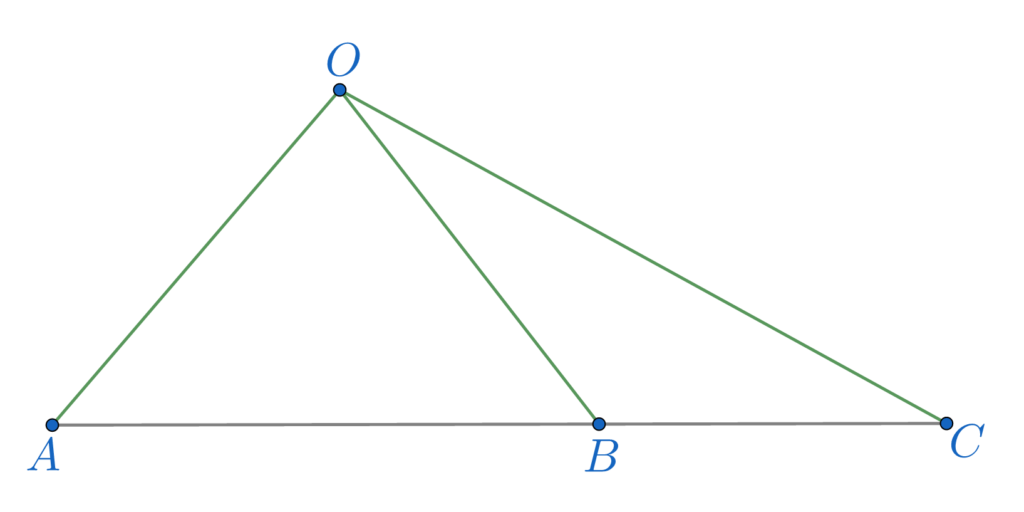
OA^2\cdot BC-OB^2\cdot AC +OC^2\cdot AB =\\\;\\=AB \cdot BC \cdot CA
7. Teorema lui Menelaus
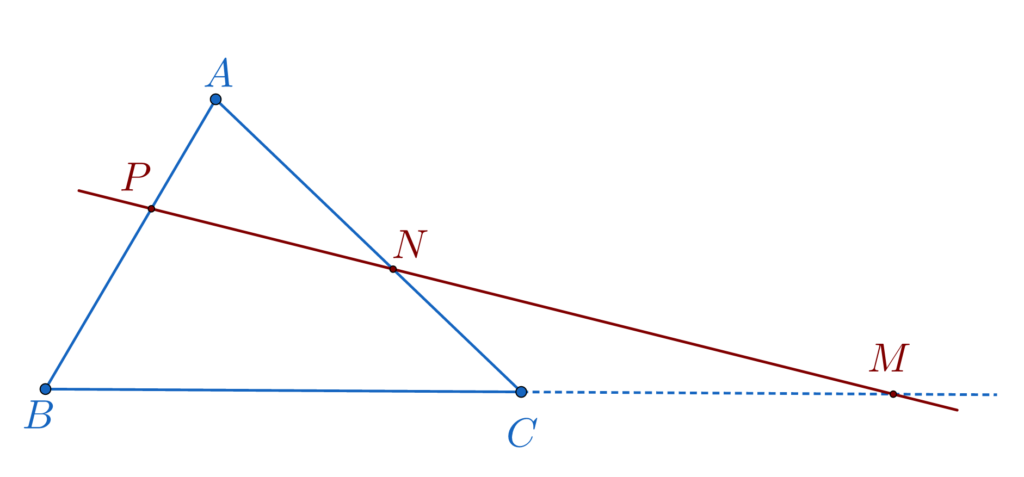
Dacă pe laturile, BC, CA și AB ale unui triunghi ABC se iau trei puncte M, N, P care verifică relația:
\frac{AP}{PB}\cdot\frac{BM}{MC}\cdot\frac{CN}{NA}=1atunci aceste trei puncte sunt colineare.
Articolul continuă pe pagina următoare