3. Mediana
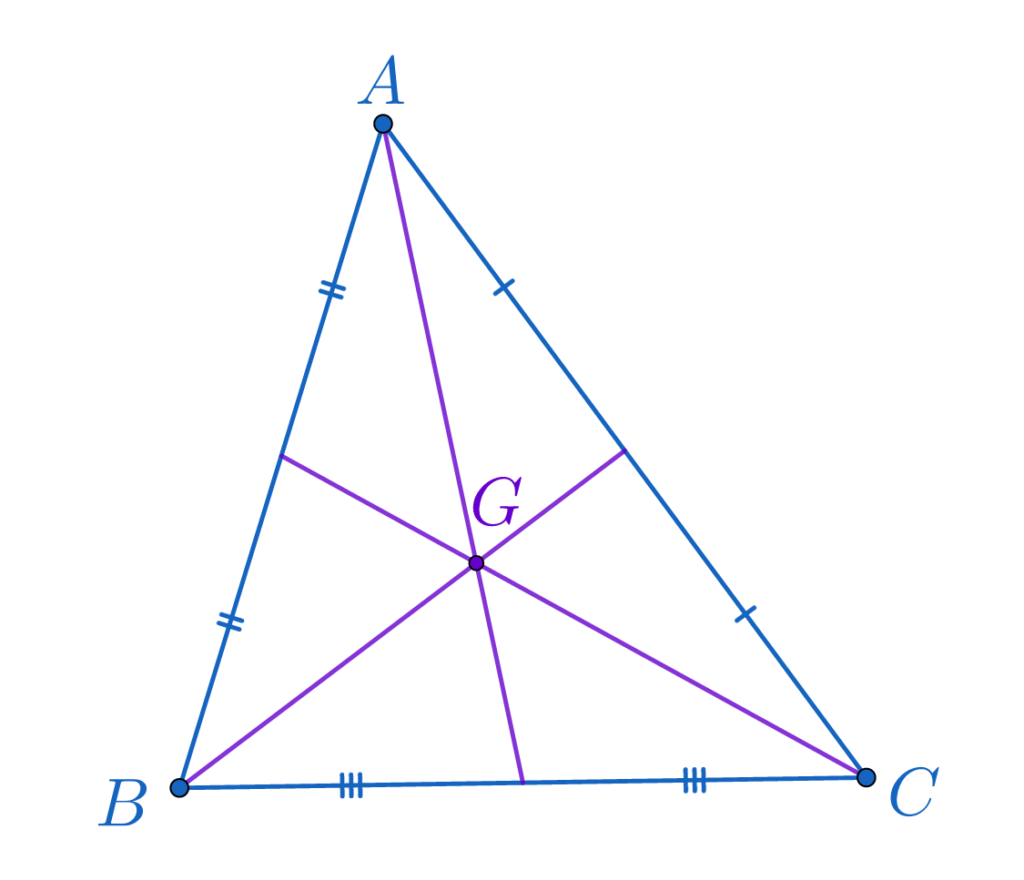
Mediana unui triunghi este segmentul determinat de un vârf al triunghiului și mijlocul laturii opuse acestuia.
Medianele unui triunghi sunt concurente in centrul de greutate al triunghiului notat G. Lungimea medianei ce pleaca din vârful A este dată de relația:
m_a^2 = \frac{2\cdot(b^2+c^2)-a^2}{4}Sunt adevărate relațiile și pentrul medianele din celelate vârfuri:
m_b^2 = \frac{2\cdot(a^2+c^2)-b^2}{4} \\\;\\ m_c^2 = \frac{2\cdot(a^2+b^2)-c^2}{4}
4. Înălțimea
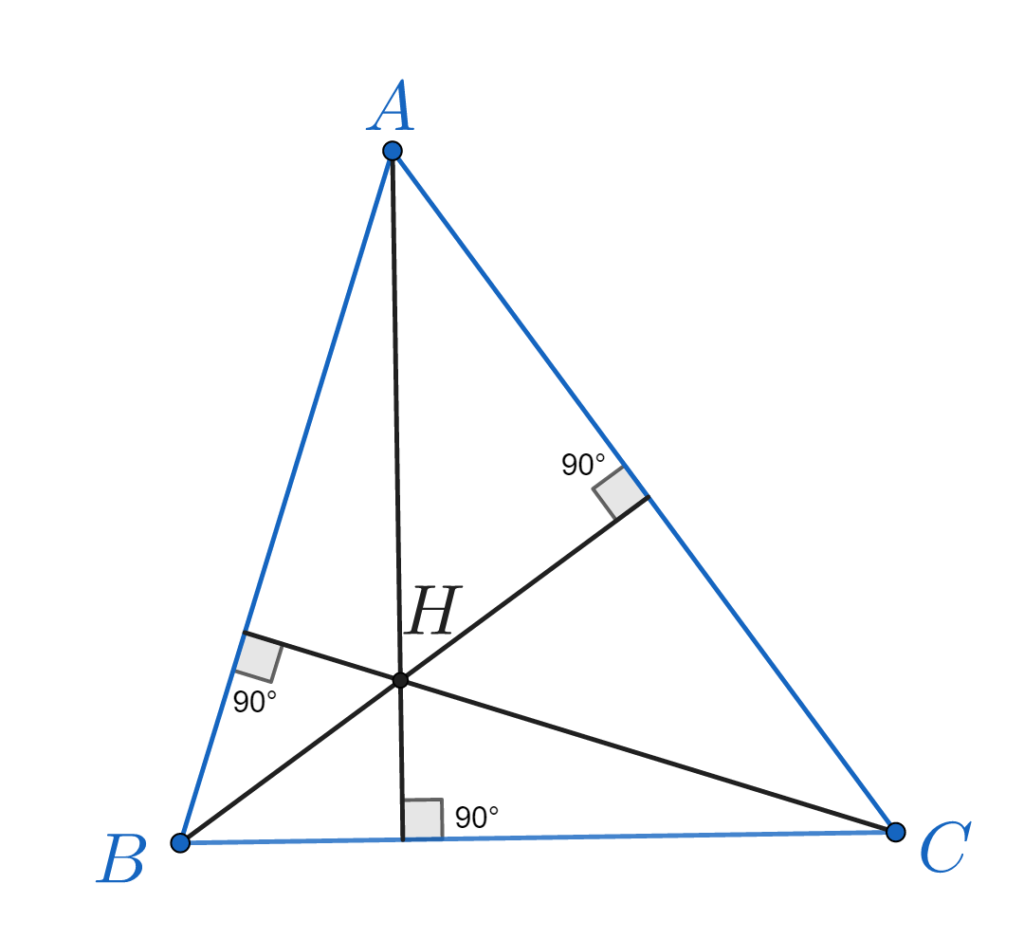
O înălțimea într-un triunghi este segmentul determinat de un vârf al triunghiului și piciorul perpendicularei din acel vârf pe latura opusă vârfului.
[the_ad_group id=”103″]
Înălțimile unui triunghi sunt concurente în ortocentrul triunghiului notat H.
h_a=b \cdot sinC =c \cdot sinB
h_a=\frac{2\cdot S}{a}Gasiți aici 10 formule pentru a calcula aria unui triunghi oarecare.
Postulatul lui Euclid
Fiind date un punct A și o drepta d, care nu trece prin A, exită o singură paralelă d care trece prin A.
Articolul continuă pe pagina următoare