7. Aria triunghiului este egală cu raportul dintre produsul pătratului lungimii laturii cu produsul sinusurilor unghiurilor adiacente laturii și dublul sinuslui unghiului opus laturii.
S = \frac{a^2\cdot sinB \cdot sinC }{2\cdot sinA} \\\;\\S = \frac{b^2\cdot sinA \cdot sinC }{2\cdot sinB} \\\;\\S = \frac{c^2\cdot sinA \cdot sinB }{2\cdot sinC} \\\;\\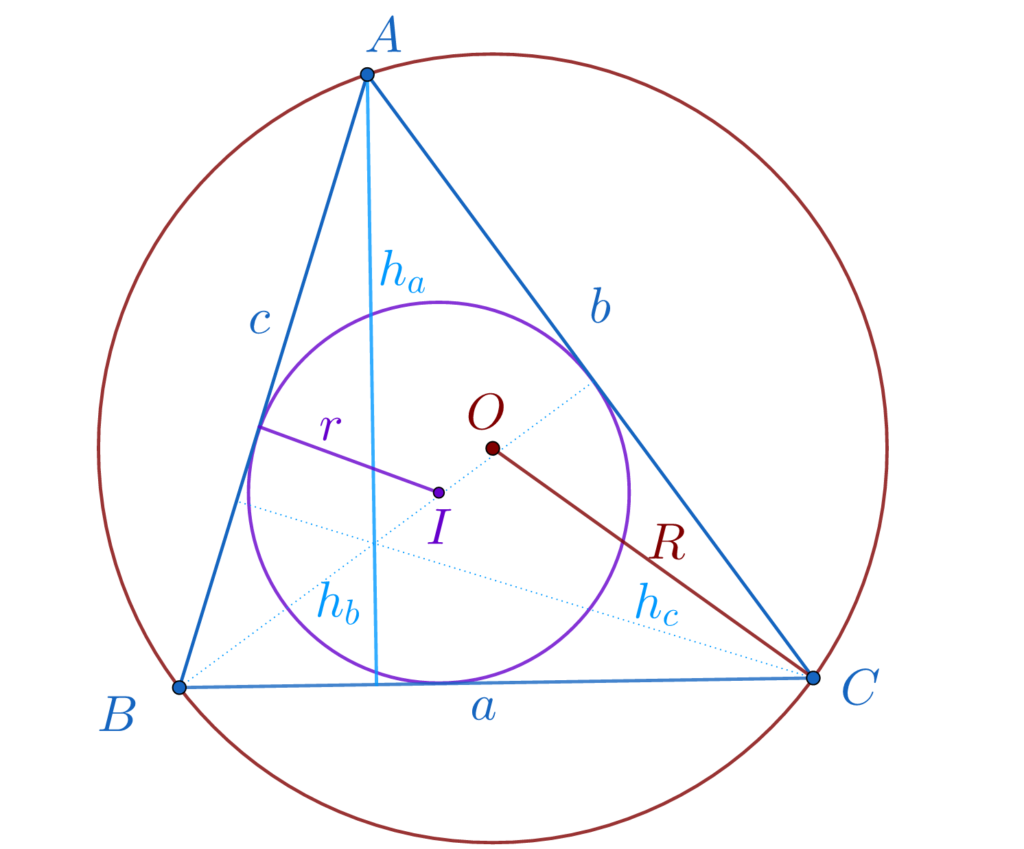
8. Aria triunghiului este egală cu raportul dintre produsul pătratului lungimii înălțimii din unghiul din care pleacă cu sinusul unghiului și dublul produsului sinusurilor celoralte două unghiuri.
S = \frac{h_{b}^2\cdot sinB }{2\cdot sinA\cdot sinC} \\\;\\S = \frac{h_{a}^2\cdot sinA }{2\cdot sinB\cdot sinC} \\\;\\S = \frac{h_{c}^2\cdot sinC }{2\cdot sinA\cdot sinB} \\\;\\
[the_ad_group id=”103″]
9. Aria triunghiului este egală cu produsul dintre pătratul semiperimetrului si tangentele jumătăților măsurilor unghiurilor triunghiului:
S =p^2\cdot{ tg \frac{A}{2} \cdot tg\frac{B}{2}\cdot tg \frac{C}{2}}\;\\\;\\\;unde\;\;p = \frac{a +b+c}{2}
10. Aria triunghiului este egală cu produsul dintre semiperimetru, diferența dintre semiperimetru și o latură și tangenta jumătății măsurii unghiului opus laturii.
S =p\cdot(p-a)\cdot tg \frac{A}{2} \\\;\\\;
S =p\cdot(p-b)\cdot tg \frac{B}{2}
\\\;\\\;
S =p\cdot(p-c)\cdot tg \frac{C}{2}
\\\;\\
\\\;\\\;unde\;\;p = \frac{a +b+c}{2}11. Raportul ariilor a două triunghiuri asemenea este egal cu pătratul raportului de asemănare al acestora.
Mai departe, poți găsi și 8 formule de bază în triunghiul dreptunghic.
[the_ad_group id=”102″]