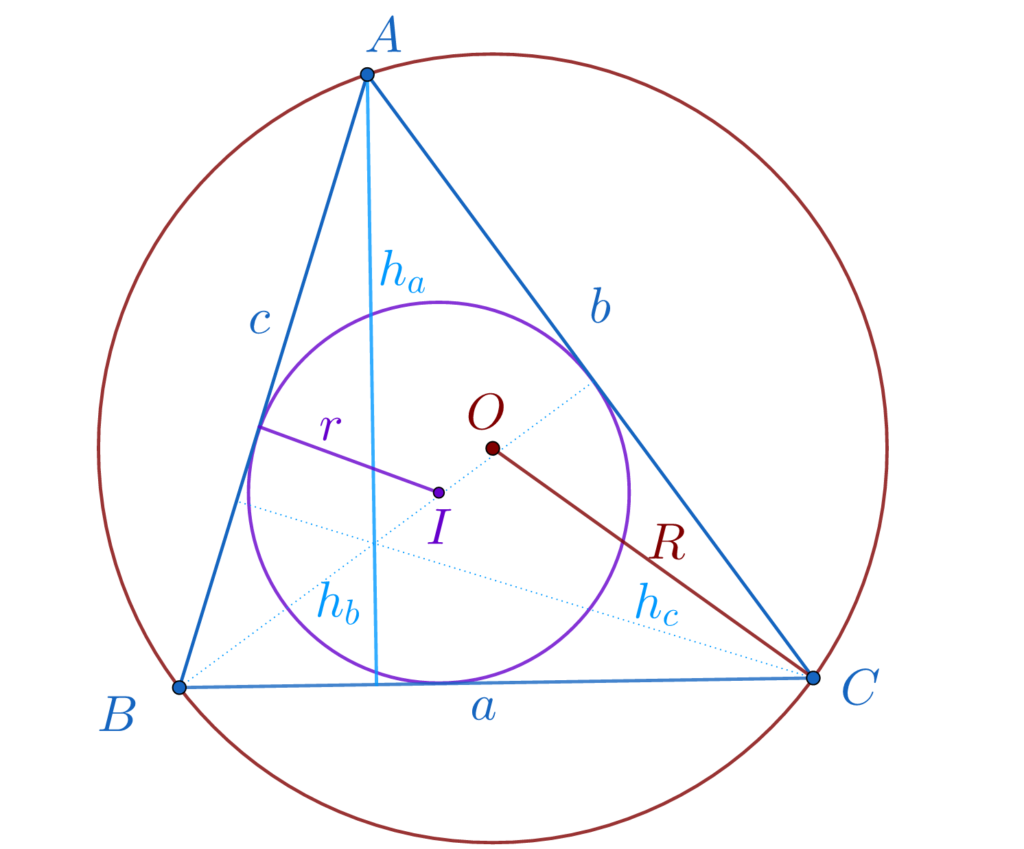
Vrem să calculăm aria triunghiului oarecare ABC: notăm cu a lungimea laturii opuse unghiului A, cu b lungimea laturii opuse unghiurilor B si c lungimea laturii opuse unghiului C; notăm cu ha lungimea înălțimii ce pleacă din vârful A. Notăm cu S – aria triunghiului ABC. Notăm cu p semiperimetrul triunghiului ABC, p = (a+b+c)/2.
Notăm cu O – centrul cercului circumscris triunghiului ABC și cu R – raza cercului circumscris triunghiului ABC; notăm cu I – cercului înscris triunghiului ABC, r -raza cercului înscris triunghiului ABC.
1. Aria triunghiului oarecare este jumătatea produsului dintre o latură și înălțimea corespunzătoare laturii.
\;\;S = \frac{a\cdot h_{a}}{2}= \frac{b\cdot h_{b}}{2}= \frac{c\cdot h_{c}}{2}2. Aria triunghiului oarecare se poate afla cu formula lui Heron: aria este egală cu radical din produsele semiperimetrului și a diferențelor dintre semiperimetru și fiecare latură.
S = \sqrt []{p\cdot(p-a)\cdot(p-b)\cdot(p-c) } \;\\\;\\\;unde\;\;p = \frac{a +b+c}{2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;
3. Aria triunghiului este egală cu produsul dintre semiperimetrul triunghiului și raza cercului înscris triunghiului.
S = p\cdot r\;\\\;\\\;unde\;\;p = \frac{a +b+c}{2}4. Aria triunghiului este egală cu raportul dintre produsul lungimii laturilor și de 4 ori lungimea razei cercului circumscris.
S = \frac{a \cdot b\cdot c}{4 \cdot R}
5. Aria triunghiului este egală cu jumătatea produsului a două laturi și sinusul unghiului dintre ele.
S = \frac{b\cdot c \cdot sinA}{2} \\\;\\ S = \frac{a\cdot b \cdot sinC}{2} \\\;\\S = \frac{a\cdot c \cdot sinB}{2}[the_ad_group id=”104″]
6. Aria triunghiului este egală cu dublul produsului pătratului razei cercului circumscris și a sinusurilor unghiurilor triunghiului.
S =2 \cdot R^2\cdot{sinA \cdot sinB \cdot sinC}
Articolul continuă pe pagina următoare