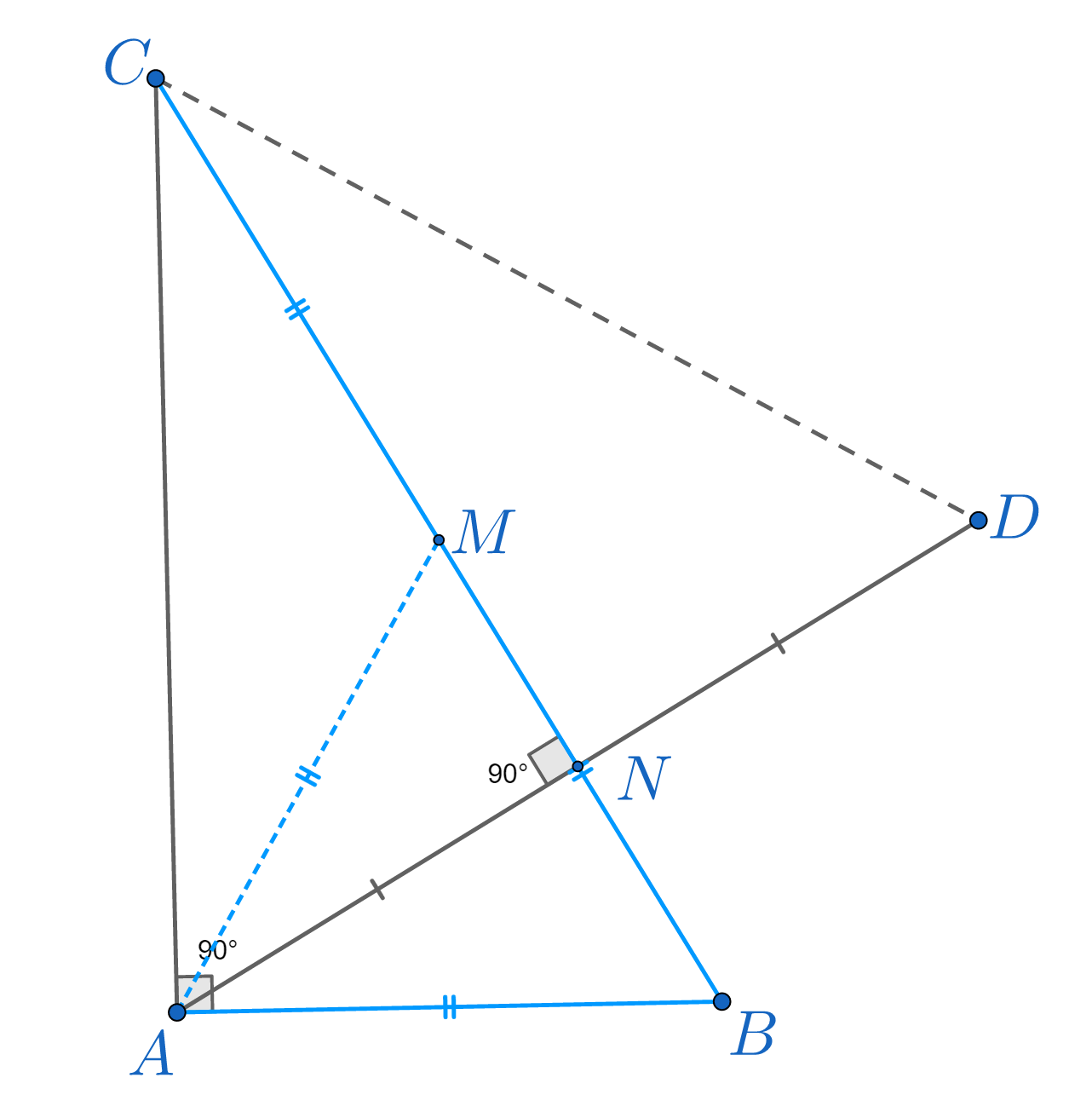
Se consideră triunghiul dreptunghic ABC. Măsura unghiului A este de 900 de grade, BC= 2AB și D simetricul lui A față de BC.
a) Demonstrați că triunghiul ACD este un triunghi echilateral.
b) Fie M piciorul medianei duse din vârful A al triunghiului ABC. Daca AM=6cm, calculați aria triunghiului ABC.
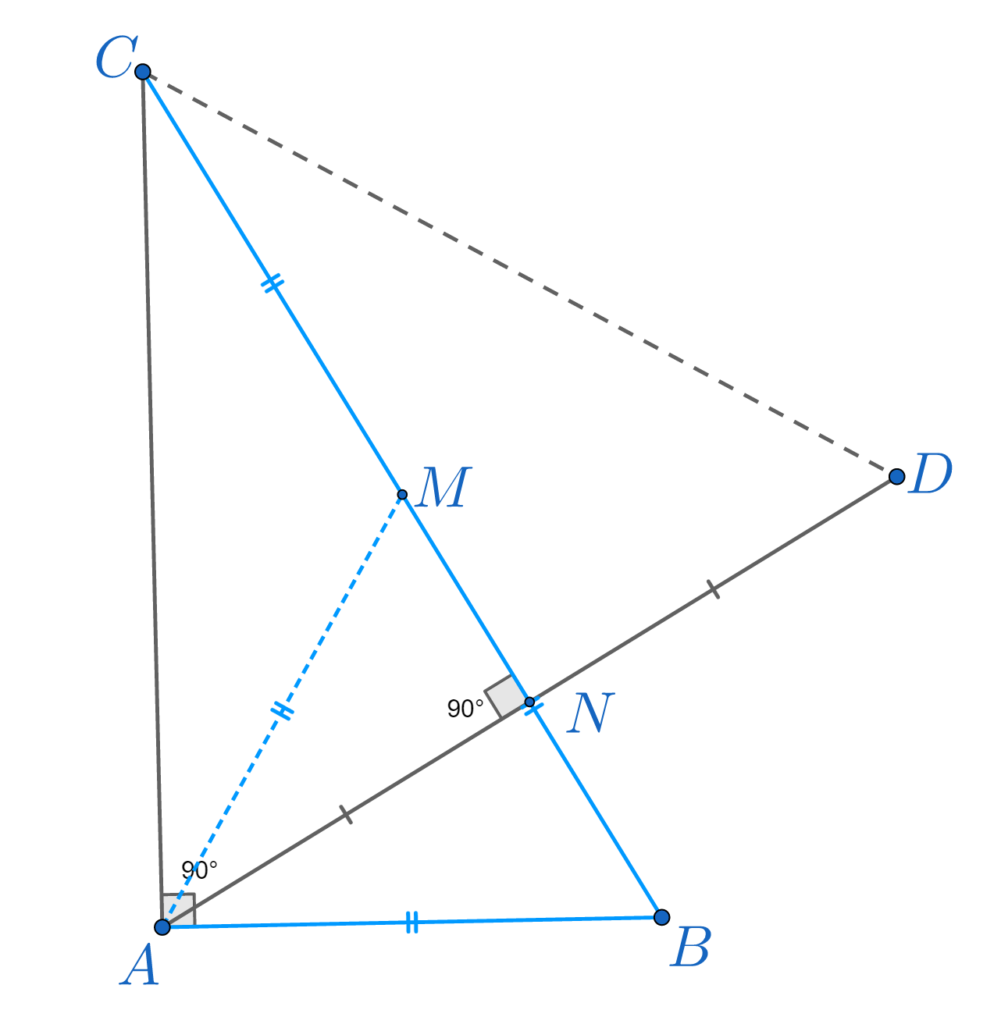
Demonstrație punctul a)
BC are de două ori lungimea lui AB. Aplicăm teorema lui Pitagora pentru a găsi lungimea catetei AC.
\left.
\begin{array}{ll} BC^2=AC^2+AB^2 \;(th. \;Pitagora)\;\\\; \\ BC=2\cdot AB\;(ipoteză) \end{array}
\right \}
\implies\;\\\; \\ \implies (2\cdot AB)^2=AC^2+AB^2 \implies\;\\\; \\ \implies 4\cdot AB^2=CA^2+AB^2 \implies\;\\\; \\ \implies 3\cdot AB^2=AC^2 \implies\;\\\; \\\implies AC = \sqrt[]{3} \cdot ABPentru a construi simetricul lui A față de BC, vom duce perpendiculara din A pe BC, notăm cu N punctul de intersecție apoi luăm punctul D pe dreaptă astfel încât AN este egal cu ND (A,N și D sunt colineare).

AN este înălțime în triunghiul dreptunghic ABC. Știm că înălțimea este egală cu raportul dintre produsul catetelor și ipotenuză, deci putem calcula lungimea inalțimii AN.
AN\perp BC\implies\;\\\\
\left.
\begin{array}{ll}\;\\\; \\ \implies \;\;AN = \frac{AC\cdot AB}{BC} \\\;\\\;\;\;\;\;\;\;\;\;\;BC = 2\cdot AB \\\;\\ \;\;\;\;\;\;\;\;\;\;AC= \sqrt[]{3} \cdot AB
\end{array}
\right \} \implies\\\;\\\implies AN = \frac{ \sqrt[]{3} \cdot AB\cdot AB}{2\cdot AB} \\\;\\
\implies AN = \frac{ \sqrt[]{3}}{2} \cdot AB 
\left.
\begin{array}{ll}
AN= ND\;\; (construcție)\;\\\\
CN \;lat. \; comună\\\;\\
m(\measuredangle CNA) =m(\measuredangle CNA) = 90^{\circ}
\end{array}
\right \}\overset{CC} {\implies} \\\;\\\\\;\\ \overset{CC}{\implies}△CNA \equiv △ CND\implies \\\;\\\\\;\\
\left.
\begin{array}{ll}
\implies AN = ND\;și\;AC = CD\\\;\\
\;\;\;\;\;\;\;\;\;AD =AN + ND = 2\cdot AN\\\;\\
\;\;\;\;\;\;\;\;\;AN = \frac{ \sqrt[]{3}}{2} \cdot AB
\end{array}
\right \}\implies\\\;\\ \;\\\implies AD= 2\cdot\frac{ \sqrt[]{3}}{2} \cdot AB\implies\\\;\\\left.
\begin{array}{ll} \implies AD= \sqrt[]{3} \cdot AB\\\;\\\;\;\;\;\;\;\;\;AC = { \sqrt[]{3}} \cdot AB \\\\\;\;\;\;\;\;\;\;AC=CD\end{array}
\right \}\implies\\\;\\ \;\\\implies AD = AC = CD \implies\\\;\\ \;\\\implies△ CAD \;△ echilateral
b) Aria unui triunghi dreptunghic este fie jumătatea produsului catetelor, fie jumătatea produsului ipotenuzei și înălțimii din unghiul drept. La punctul a) am calculat atât dimensiunea catetei AC cât și dimensiunea înălțimii AN.
Știm că mediana într-un triunghi dreptunghic este jumătate din ipotenuză.
\left.
\begin{array}{ll}
AM= \frac{BC}{2} (mediana \;△\;dr)\;\\\; \\ AB = \frac{BC}{2} \;(ipoteză)
\end{array}
\right \}
\implies\;\\\; \\
\left.
\begin{array}{ll}
\implies AB = BM =MA \\\;\\
\;\;\;\;\;\;\;\;\;AM = 6\end{array}
\right \}
\implies\;\\\;\\ \left.
\begin{array}{ll}\implies AB = 6 \\\;\\ \;\;\;\;\;\;\;\;\ AC = { \sqrt[]{3}} \cdot AB\end{array}
\right \} \implies\;\\\; \\\implies AC = { \sqrt[]{3}} \cdot 6 \\\;\\S = \frac{AC\cdot AB}{2} \implies\;\\\; \\\implies S = \frac{{ \sqrt[]{3}} \cdot 6\cdot6}{2} \implies\\\; \\\implies S ={ \sqrt[]{3}} \cdot 18