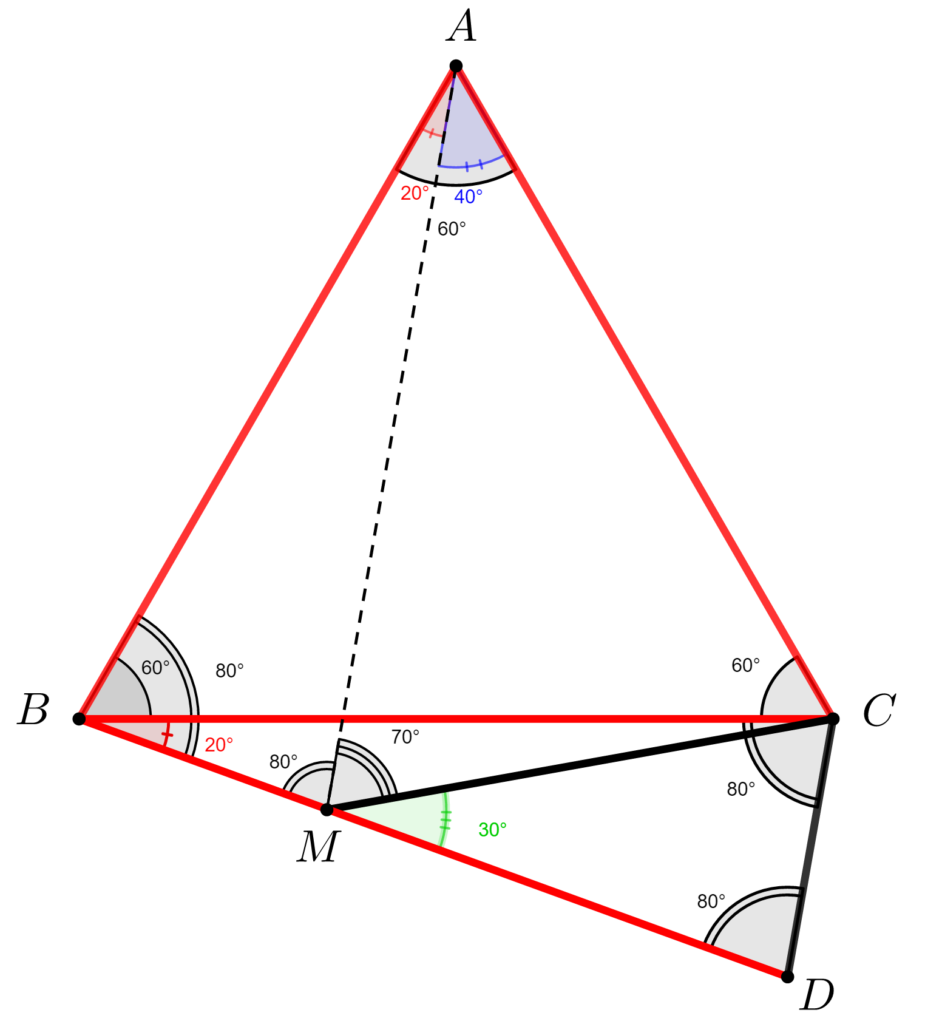
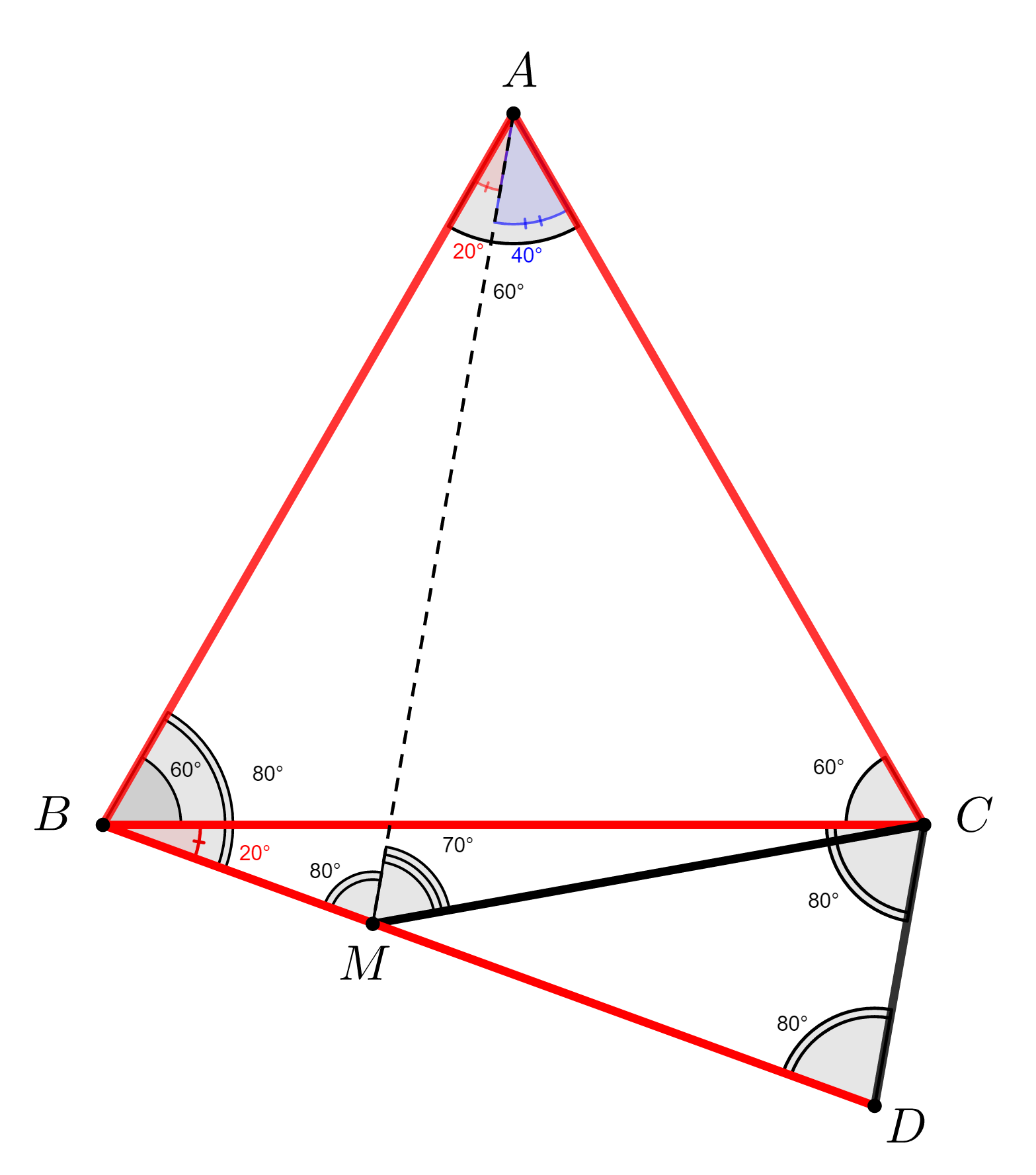
Fie \;ABC \;un \;triunghi \;echilateral\; și\; punctul \;D\; astfel \;încât\;\;\;\;\;\; \\BD = BC, \;m(\measuredangle CBD) = 20^{\circ}\; iar\; punctele \;A\; şi \;D\; sunt \;situate\;\;\\de \;o \;parte \;și \;de\; alta \;a\; dreptei \;BC.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\Fie M \in [ \,BD ] \, astfel\; încât\; BM = DC.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\Aflați \;m(\measuredangle DMC).\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;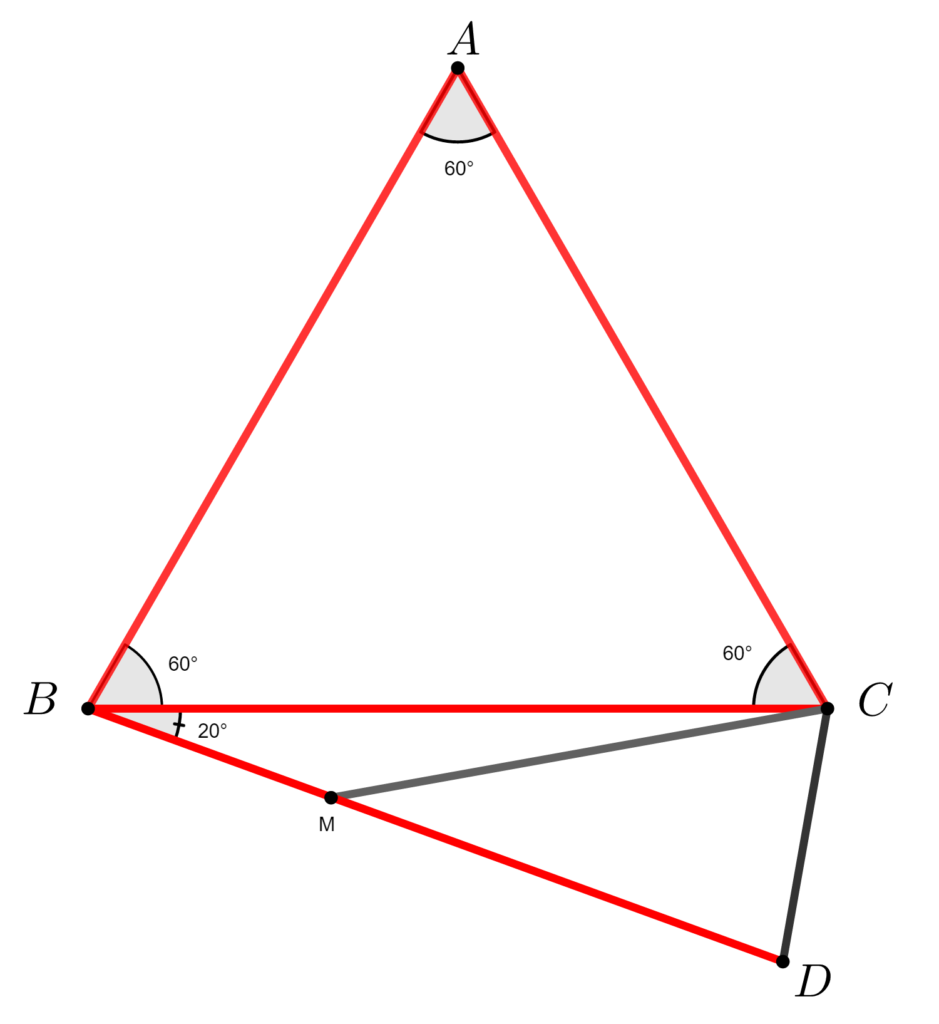
Pentru a găsi măsura unghiului DMC vom uni pe A cu M și vom calcula măsurile unghiurilor AMB si AMC.
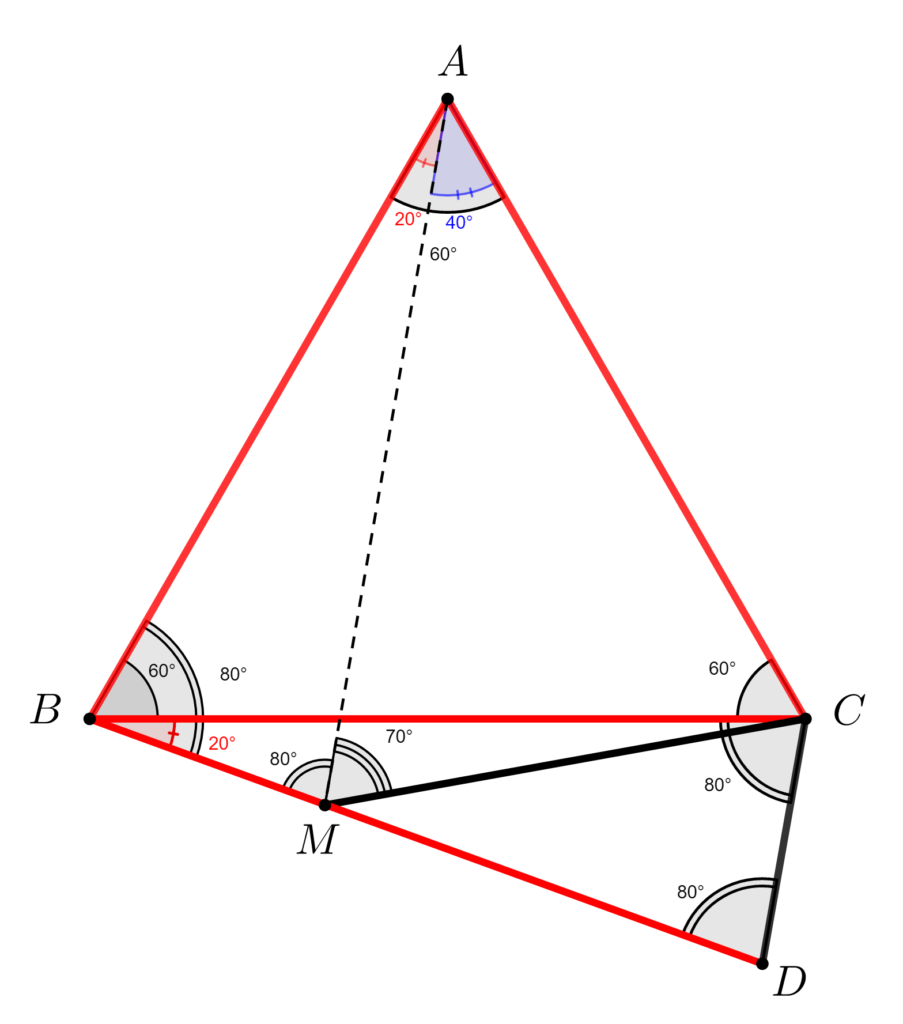
\left.
\begin{array}{ll}
m(\measuredangle DBC)\;=\; 20^{\circ} (din\;ipoteză)\\\;\\
m(\measuredangle ABC)\;=\; 60^{\circ}(△ ABC\; △ echilateral) \\
\;\;\;\;\;\;\;\;\\m(\measuredangle ABM)\; = \; m(\measuredangle ABC) + m(\measuredangle CBM)\\\;\\
\end{array}
\right \}
\implies\;\\\; \\ \implies m(\measuredangle ABM)\; = 60^{\circ} \;+\;20^{\circ} \implies\;m(\measuredangle ABM)\; = 80^{\circ}\\ \;\\ \;\\
BC = BD\;(din\;ipoteza) {\implies}△ CBD\; △isoscel\implies\;\;\;\;\;\;\;\;\;\;\;\;\;\\\;\\
\left.
\begin{array}{ll}
\implies \;m(\measuredangle BCD)\;=\;m(\measuredangle CDB)\; \\ \\
\;\;\;\;\;\;\;\;\;\;m(\measuredangle DBC)\;=\; 20^{\circ}\;(din\; ipoteză)
\\ \\\;\;\;\;\;\;\;\;\;\;m(\measuredangle CBD)\; + \; m(\measuredangle CDB) + m(\measuredangle DCB) = 180^{\circ}\\\;\\
\end{array}
\right \}
\implies\; \\\;\\\implies2 \cdot m(\measuredangle CDB) + 20^{\circ} = 180^{\circ} \implies\; 2 \cdot m(\measuredangle CDB) = 160^{\circ} \implies\;\\\;\\\implies\; m(\measuredangle CDB) = 80^{\circ} \left.
\begin{array}{ll}
\left.
\begin{array}{ll}
m(\measuredangle ABM)\; = 80^{\circ} \\ \;\\ m(\measuredangle CDB) = 80^{\circ}
\end{array}
\right \} \implies m(\measuredangle ABM)\; =\;m(\measuredangle CDB)
\\\;\\\\\;\\
\left.
\begin{array}{ll}
△ ABC\; △ echilateral\implies AB = BC\\\;\\
BC = BD \;(din\; ipoteză)
\end{array}
\right \} \implies AB = BD\;\\\;\\\\\;\\
BM = CD \;(din\;ipoteză)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;
\end{array}
\right \} \overset{LUL} {\implies} \\ \; \\\ \;\\\overset{LUL} {\implies}\;△ABM\;{\displaystyle \equiv }\;△BDC\implies \\ \;\\ \;\\
\left.
\begin{array}{ll}
\implies m(\measuredangle AMB)\; = m(\measuredangle BCD) \\\;\\
\;\;\;\;\;\;\;\;\;m(\measuredangle BCD) = 80^{\circ}
\end{array}
\right \} \implies m(\measuredangle AMB) = 80^{\circ} \\\;\\\;\\
\left.
\begin{array}{ll}
m(\measuredangle AMB) = 80^{\circ}\\\;\\
m(\measuredangle ABM) = 80^{\circ}
\end{array}
\right \} \implies △BAM\;△isoscel
\left.
\begin{array}{ll}
△ABM\;{\displaystyle \equiv }\;△BDC\implies m(\measuredangle BAM) = m(\measuredangle DBC) \\\;\\
m(\measuredangle CBD) = 20^{\circ} (ipoteză)
\end{array}
\right \} \implies \\\;\\\;\\
\left.
\begin{array}{ll}
\implies m(\measuredangle BAM) = 20^{\circ}
\\\;\\
\;\;\;\;\;\;\;\;\;m(\measuredangle BAC)\;=\; 60^{\circ}(△ ABC\; △ echilateral)
\\\;\\
\;\;\;\;\;\;\;\;\;m(\measuredangle BAC) = m(\measuredangle BAM) \;+\; m(\measuredangle MAC)
\end{array}
\right \} \implies \\\;\\\implies m(\measuredangle MAC) = m(\measuredangle BAC)\;-\;m(\measuredangle BAM) \implies \\\;\\\implies m(\measuredangle MAC)\; =\; 60^{\circ}\;-\;20^{\circ}\implies m(\measuredangle MAC)\; =\; 40^{\circ}
\left.
\begin{array}{ll}
△BAM\;△isoscel\implies AB \;= \;AM \\\;\\
△ABC\;△echilateral\implies AB\; = \;AC
\end{array}
\right \} \implies \\\;\\\;\\ \implies AM=AC \implies △MAC\;△isoscel \implies \\\;\\
\left.
\begin{array}{ll}
\implies m(\measuredangle AMC) = m(\measuredangle ACM)\;
\\\;\\
\;\;\;\;\;\;\;\;\;m(\measuredangle MAC)\; =\; 40^{\circ}\\\;\\
\;\;\;\;\;\;\;\;\;m(\measuredangle MAC) + m(\measuredangle ACM) \;+\; m(\measuredangle CMA) \; =\; 180^{\circ}\\\;\\
\end{array}
\right \} \implies \\\;\\\implies 40^{\circ} + 2 \cdot m(\measuredangle AMC) = 180^{\circ} \implies 2 \cdot m(\measuredangle AMC) = 140^{\circ}\implies \;\\\\\;\\\implies m(\measuredangle AMC)\; =\; 70^{\circ}
\left.
\begin{array}{ll}
m(\measuredangle BMA) + m(\measuredangle AMC) \;+\; m(\measuredangle CMD) \; =\; 180^{\circ}\\\;\\
m(\measuredangle AMB) \;= \;80^{\circ}\;\\\;\\
m(\measuredangle MAC)\; =\; 70^{\circ}
\end{array}
\right \} \implies \\\;\;\\\implies m(\measuredangle CMD) =180^{\circ}-m(\measuredangle BMA)-m(\measuredangle AMC) \;\implies\\\;\\\implies m(\measuredangle CMD) =\;180^{\circ}-\;80^{\circ}\;\;-70^{\circ}\;\;\implies\\\;\\\implies m(\measuredangle CMD) =\;30^{\circ}