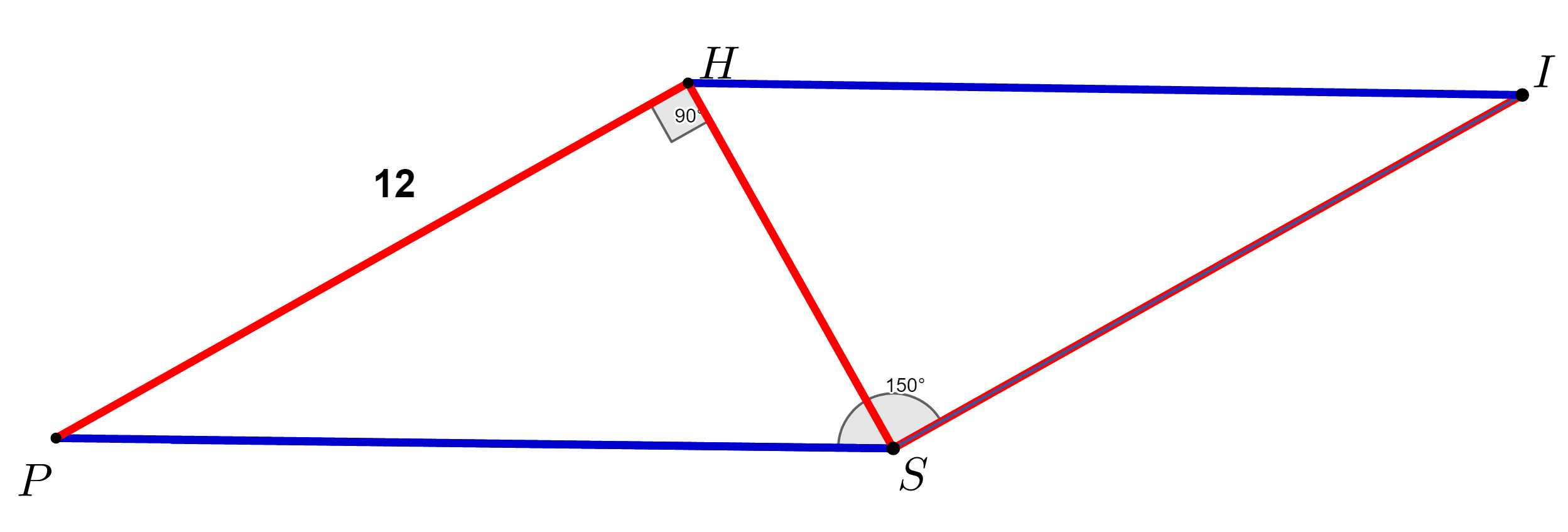
În\; paralelogramul \;PSIH \;se \;dau \;PH = 12 cm \;și \;m(\measuredangle PSI)=150^{\circ}. \;\\Aflați\; aria\; paralelogramului\; ştiind \;că \;HS\perp HP.
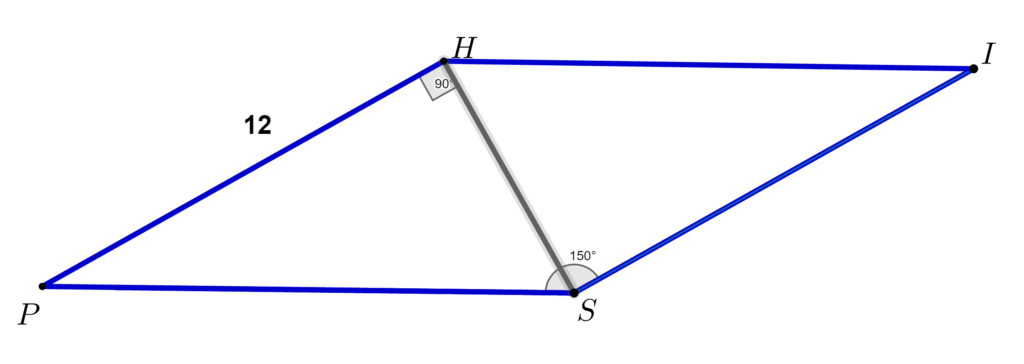
Pentru a calcula aria paralelogramului putem calcula aria celor două triunghiuri dreptunghice PHS si ISH.
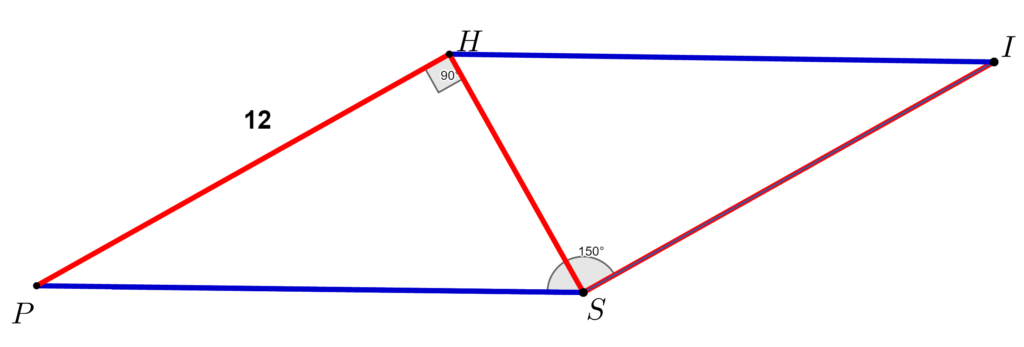
Cele două triunghiuri au arii egale ele fiind congruente. O metodă pentru a demonstra această congruență este următoarea:
\left.
\begin{array}{ll}
\left.
\begin{array}{ll}
PH\;{\parallel }\;SI \\\;\\HS\;secanta
\end{array}
\right \}\overset{alterne\;interne} {\implies} m(\measuredangle PHS)= m(\measuredangle HSI)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;m(\measuredangle PHS)=90^{\circ}
\end{array}
\right \} \implies\\\;\\\implies m(\measuredangle HSI) = 90^{\circ}
\left.
\begin{array}{ll}
PH = SI (laturi\; opuse \;paralelogram)\\\\HS\; latură\; comună\\\\
m(\measuredangle PHS)= m(\measuredangle HSI) = 90^{\circ}
\end{array}
\right \} \overset{Catetă\; Catetă} {\implies}\\\;\\ \implies △PSH{\displaystyle \equiv }△IHS
Deci este suficient să calculăm aria unuia dintre ele, de exemplu aria triunghiul dreptunghic PHS, care este jumătetea produsului catetelor.
S_{ △PSH} = \frac{PH\cdot HS}{2} Știm care este lungimea unei catete și ne vom folosi de masurile unghiurilor triunghiului dreptunghic pentru a afla dimensiunea celeilate catete.
\left.
\begin{array}{ll}
m(\measuredangle HSI) = 90 ^{\circ} \\\\
m(\measuredangle PSI) = 150 ^{\circ} \\\\
m(\measuredangle HSP) = m(\measuredangle PSI) - m(\measuredangle HSI)
\end{array}
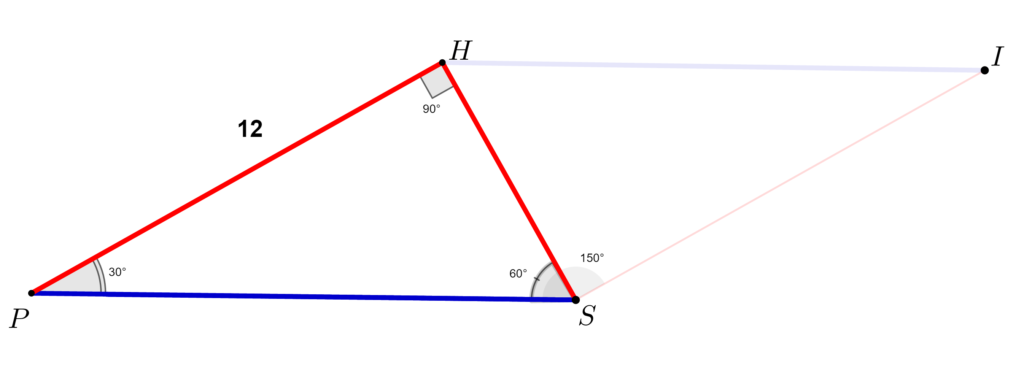
\right \}{\implies} \\\;\\ \implies m(\measuredangle HSP) = 150 ^{\circ} - 90 ^{\circ} \implies m(\measuredangle HSP) = 60 ^{\circ}
Într-un triunghi dreptunghic, suma unghiurilor care nu au 90 de grade este 90 de grade.
\left.
\begin{array}{ll}
m(\measuredangle HSP ) + m(\measuredangle HPS) = 90 ^{\circ} \\\\
m(\measuredangle HSP) = 60 ^{\circ}
\end{array}
\right \} \implies \\\;\\ \implies m(\measuredangle HPS) = 90 ^{\circ} - 60 ^{\circ} \implies m(\measuredangle HPS) = 30 ^{\circ}În acest triunghi, știm ca măsura unghiului HPS este de 30 de grade deasemenea știm că dimensiunea catetei opuse unghiului de 30 de grade este jumătate din dimensiunea ipotenuzei. Iar din teorema lui Pitagora stim că suma pătratelor catetelor este egală cu pătratul ipotenuzei.
\left.
\begin{array}{ll}
\left.
\begin{array}{ll}
m(\measuredangle HPS) = 30 ^{\circ} \\\\
△PHS\; este\; △\;dreptunghic
\end{array}
\right \}\overset{Th. \measuredangle 30 ^{\circ}} {\implies} HS =\frac{PS}{2} \\\;\\
△PHS\; este\; △ \;dreptunghic
\overset{Th. Pitagora} {\implies} PS^2 = PH^2 +HS^2\\\;\\
PH = 12
\end{array}
\right \}{\implies}\\\;\\\implies
(2\cdot HS)^2= 12^2 +HS^2\;\implies 4\cdot HS ^2= 144 +HS^2\implies \\\;\\\\ \implies 3\cdot HS ^2= 144 \implies HS ^2= \frac{144}{3} \implies HS = \frac{12}{ \sqrt3} \implies \\\;\\\\ \implies HS = \frac{12\sqrt3}{ 3} \implies HS = 4\sqrt3
Aria paralelogramului este de două ori aria triunghiului dreptunghic PHS.
S_{ PSIH} = 2\cdot \frac{PH\cdot HS}{2} \implies \\\;\\
\left.
\begin{array}{ll}
\implies S_{ PSIH} = PH\cdot HS\\\\\;\;\;\;\;\;\;\;\;\;HS = 4\sqrt3 \\\;\\
\;\;\;\;\;\;\;\;\;PH = 12
\end{array}
\right \} \implies S_{ PSIH} =12\cdot 4\sqrt3 \implies \\\;\\ \implies S_{ PSIH} = 48\sqrt3