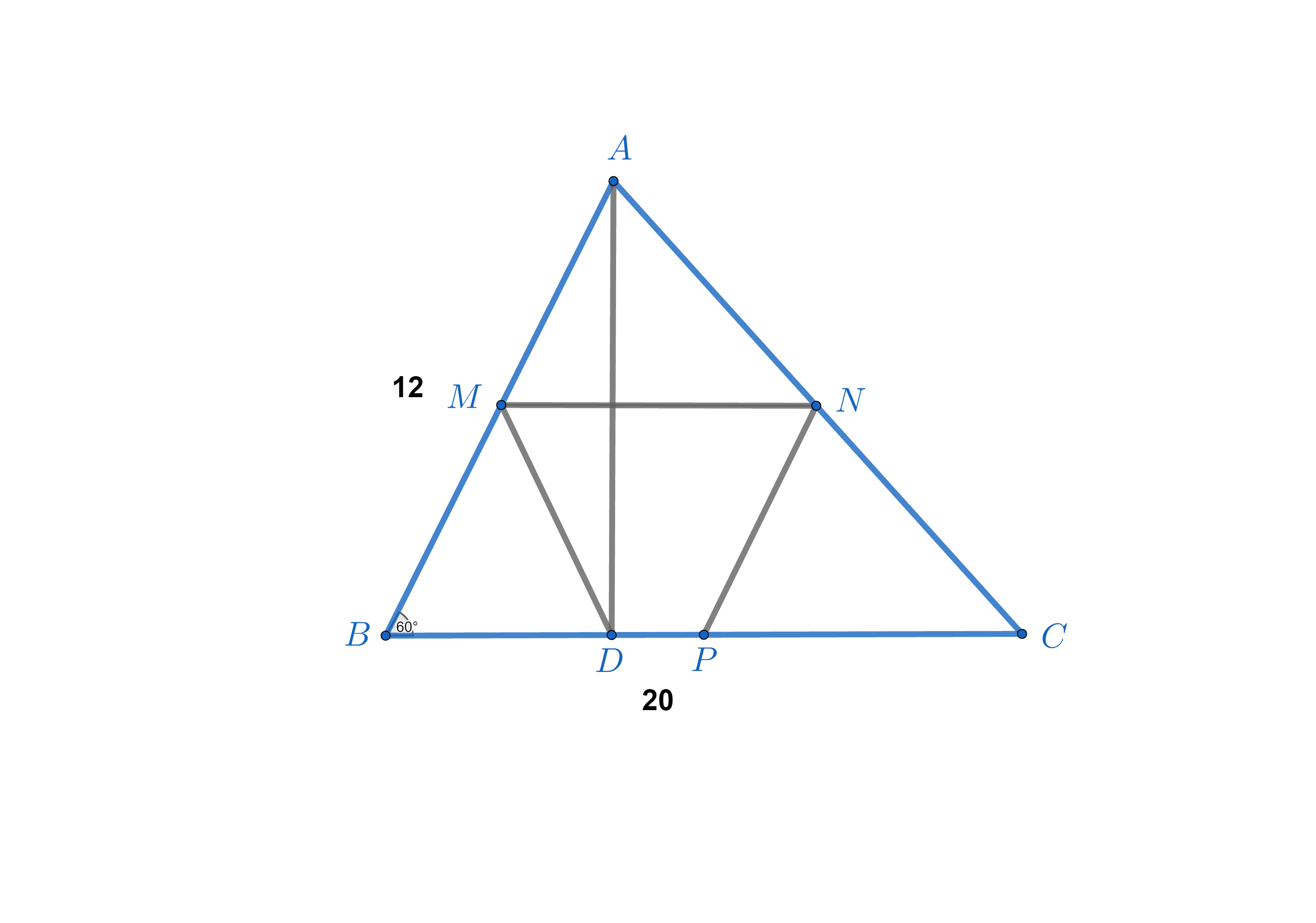
În figura alăturată este reprezentat triunghiul ABC, având AB = 12 cm, BC = 20 cm și măsura unghiului ABC egală cu 60°. Notăm cu M, N, P mijloacele segmentelor AB, AC, respectiv BC şi cu D piciorul înălțimii din A.
a) Arată că MD = NP = 6 cm.
b) Determină perimetrul patrulaterului MNPD.
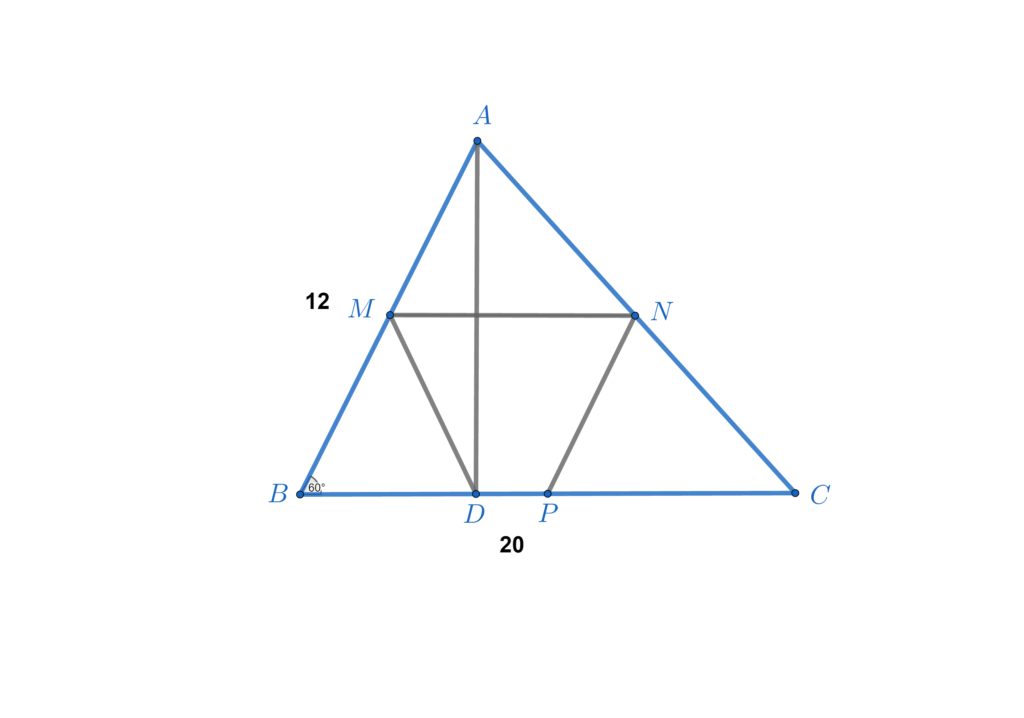
Demonstrație punctul a:
- deoarece N și P sunt mijloacele laturilor AC, respectiv BC, NP va fi linie mijlocie în raport cu AB deci va fi egală cu jumătate din AB și paralelă cu AB.
NP = \frac{AB}{2}
\implies NP = \frac{12}{2} \implies NP = 6
NP {\parallel }AB
- deoarece triunghiul BDA este triunghi dreptunghic și MD este mediană în triunghiul dreptunghic MD, va fi jumătate din AB.
MD = \frac{AB}{2} \implies MD = \frac{12
}{2} \implies MD=6De aici rezultă că
MD = NP = 6 cm
Demonstrație punctul b:
MD = MB \implies \vartriangle MBD \vartriangle isoscel \\ și \\\measuredangle (MBD) = 60 ^{\circ} \\ deci \vartriangle MBD \;
este \; \vartriangle echilateral- deoarece N și M sunt mijloacele laturilor AC respectiv AB, NM va fi linie mijlocie in triunghi, deci va fi egală cu jumătate din BC și paralelă cu BC.
NM = \frac{BC}{2}
\implies NM = \frac{20}{2} \implies NM = 10
NM {\parallel }BC
Pentru a calcula perimetrul lui DPNM mai trebuie să calculăm lungimea segmentului DP. Acesta se poate calcula în mai multe moduri.
- O soluție ar putea fi să ducem perpendiculara din P pe MN și să notăm cu F punctul de intersecție. De asemenea vom nota cu E intersecția lui AD cu MN, ca în figura de mai jos:
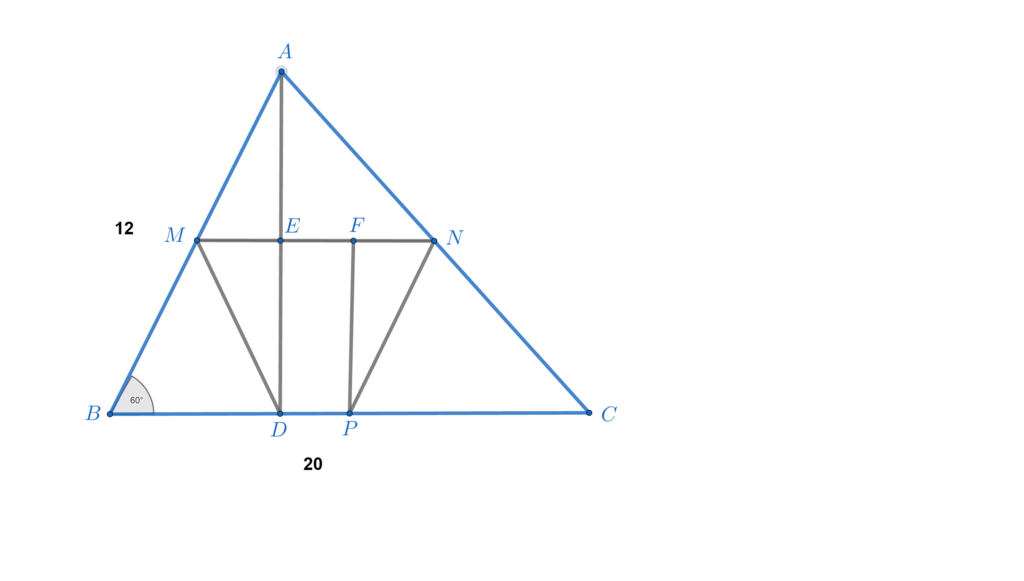
Știm că:
NM {\parallel }BC \\
AD\perp BC\\ \implies \; AD\perp MN
\;PF\perp MN\;(din \;construcție)\\DE {\perp}MN \\ \implies\; FP\parallel DE\;dar\;NM\; {\parallel }BC \\⟹FPDE \;paralelogram\;cu\; un\; unghi\; drept \\
\implies FPDE \;dreptunghi
\implies\; DP = EF \;și\; ED =FP
La\;punctul\;a)\;am\;demonstrat\;că\;MD = NP, \\ știm\; că\;ED=FP \\ \; \\\implies △MDE {\displaystyle \equiv }△NPF (triunghiuri\;dreptunghice) \\ \implies ME =FN
ME este de asemenea linie mijlocie în triunghiul ADB
ME= \frac{BD}{2} \\ \; \\BD=6 ( \vartriangle MBD\;echilateral) \\ \; \\\implies ME= \frac{6}{2}\implies ME = 3
ME = FN = 3 \\ dar\\ EF =MN - ME -FN \implies EF = 10-3-3\\ \implies EF = 4
EF =DP \implies DP = 4
Perimetrul va fi:
MD + DP +PN+NM = 6+ 4 + 6+10 = 26
- O altă soluție pentru a calcula lungimea segmentului DP ar putea fi să facem diferența între lungimea segmentului BP și lungimea lui BD.
BP=PC\\ \;\\BC =20 \implies BP=\frac{BC}{2}\implies BP = \frac{20}{2} = 10\vartriangle MBD\;echilateral \\ \implies BD = 6
DP = BP -BD \implies DP = 10-6\\\implies DP =4
Perimetrul va fi, la fel ca mai sus:
MD + DP +PN+NM = 6+ 4 + 6+10 = 26